Нормальное распределение в реальном мире
Похожие статьи вашей тематики
Нормальное распределение или нечто близкое к нему часто имеет место в самых разных практических сферах. Из-за того оно и названо нормальным.
Применительно к социальной сфере, скажем, нормальное распределение неплохо описывает распределение интеллекта и знаний среди населения. 80-90% народу по уровню находятся в положении «средненько», «так себе». Полные идиоты (или почти полные) находятся в суровом меньшинстве слева на графике, как и очень умные люди справа на графике, который можно изобразить примерно так:

В результате прогрессивных преобразований в обществе (если такие действительно имеют место, что обычно связывают с прогрессивным развитие общества) «колокол» смещается вправо:
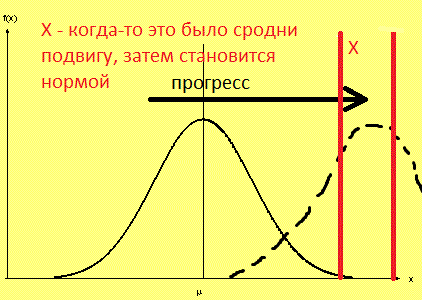
То, что когда-то считалось почти нереальным и достигалось немногими, может стать нормой. И наоборот, того, чего раньше было достаточно и на чём и останавливались почти все, теперь уже не хватает. При «откате», регрессивных и губительных для общества изменениях колокол смещается влево, потому что нормой становится то, что ранее было присуще глупым и малообразованным индивидам.
Функция Лапласа
Доказано, что невозможно выразить через элементарные функции функцию распределения (интегральной функции) нормальной случайной величины:
 , ,
где 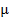 - это математическое ожидание этой случайной величины, а - это математическое ожидание этой случайной величины, а  - её стандартное квадратичное отклонение. Однако для расчетов, связанных с нормальной случайной величиной, необходимо знать её значения. Для этих целей вводится функция Лапласа: - её стандартное квадратичное отклонение. Однако для расчетов, связанных с нормальной случайной величиной, необходимо знать её значения. Для этих целей вводится функция Лапласа:
 . .
Для функции Лапласа составлены таблицы значений, которые можно найти в учебнике или задачнике по теории вероятностей. Кроме того, значения этой функции можно вычислить в некоторых современных электронных таблицах. Но, например, в Microsoft Excel, поскольку функции Лапласа нет, вместо неё необходимо использовать функцию стандартного нормального распределения, которая в русскоязычной версии этой программы называется НОРМСТРАСП, и её значения вычисляются по формуле: 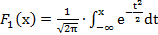 . Тогда получается . Тогда получается 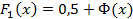 . Причина в том, что поскольку . Причина в том, что поскольку  как полная вероятность на всей действительной оси, а в силу симметрии функции стандартного нормального распределения половина полной вероятности будет равна как полная вероятность на всей действительной оси, а в силу симметрии функции стандартного нормального распределения половина полной вероятности будет равна  . Тогда по свойствам определённого интеграла . Тогда по свойствам определённого интеграла  . .
График функции Лапласа является примерно следующим:

Рисунок. График функции Лапласа.
При использовании таблиц значений функции Лапласа следует учитывать, что эта функция обладает следующими свойствами:
1. По графику функции Лапласа видно, что эта функция имеет значения от -0,5 до 0,5 эти значения не достигая, а асимптотически к ним приближаясь: к -0,5, при  , а к 0,5, при , а к 0,5, при  . .
2.  . .
3.  . .
4.  , т.е. функция Лапласа является нечетной, поэтому в таблицах приведены значения этой функции только для положительных значений аргумента. Для отрицательных значений аргумента значения функции Лапласа определяются из её нечетности. , т.е. функция Лапласа является нечетной, поэтому в таблицах приведены значения этой функции только для положительных значений аргумента. Для отрицательных значений аргумента значения функции Лапласа определяются из её нечетности.
5. Функция Лапласа является возрастающей, потому что её производная от определённого интеграла по верхнему пределу равна подынтегральной функции:  , а эта функция больше нуля на всей своей области определения, поскольку является показательной. , а эта функция больше нуля на всей своей области определения, поскольку является показательной.
6. При  значение функции Лапласа значение функции Лапласа  , поэтому в приближённых вычислениях при , поэтому в приближённых вычислениях при 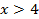 принято считать, что принято считать, что 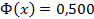 с точностью до тысячных. с точностью до тысячных.
|