
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выборочное среднее как статистическая оценка среднего в генеральной совокупности
Пусть сделана выборка Обозначим Докажем, что выборочное среднее является несмещённой оценкой среднего генеральной совокупности.
Таким образом получилось, что Можно доказать, что выборочное среднее является также эффективной и состоятельной оценкой средней генеральной совокупности. Вычислим дисперсию для выборочной средней.
В результате Эти рассуждения и доказательства проведены в предположении, что выборка является повторной, только такие выборки позволяют каждый раз отбирать элемент генеральной совокупности независимо от предыдущих выборов. В случае повторной выборки достаточно большого объёма (большего 30) можно доказать, что случайная величина выборочное среднее
В реальной ситуации выборку чаще всего делают бесповторной, чтобы получить в выборке большее разнообразие информации. Можно доказать, что и в случае бесповторной выборки выборочное среднее является несмещённой оценкой генерального среднего. Формулы для определения выборочного среднего для бесповторной выборки не меняются. Более того, если объём бесповторной выборки достаточно велик, но при этом выборка составляет незначительную долю генеральной совокупности, что бывает в очень больших генеральных совокупностях, то и в этом случае закон распределения выборочной средней Но в случае бесповторной выборки необходимо изменить формулы вычисления дисперсии и стандартного квадратичного отклонения выборочной средней Сравнение формул для повторной и для бесповторной выборок показывает, что дисперсия и стандартное квадратичное отклонение выборочной средней для бесповторной выборки меньше при одинаковом объёме выборки. Это означает, что бесповторная выборка более эффективна, чем повторная. Но этот эффект проявляется лучше для сравнительно небольших выборок.
|
|||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 973; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.25.73 (0.005 с.) |
 из распределения
из распределения 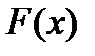 для случайной величины
для случайной величины  . Независимые измерения или наблюдения
. Независимые измерения или наблюдения 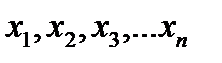 являются реализацией этой выборки.
являются реализацией этой выборки.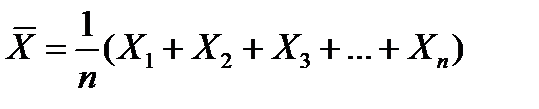 . Статистика
. Статистика  называется выборочным средним и используется в качестве точечной оценки среднего генеральной совокупности.
называется выборочным средним и используется в качестве точечной оценки среднего генеральной совокупности.  .
.
 , т.е. математическое ожидание выборочного среднего равно математическому ожиданию или среднему значений в генеральной совокупности. Следовательно, выборочная средняя – это несмещённая оценка среднего в генеральной совокупности.
, т.е. математическое ожидание выборочного среднего равно математическому ожиданию или среднему значений в генеральной совокупности. Следовательно, выборочная средняя – это несмещённая оценка среднего в генеральной совокупности.
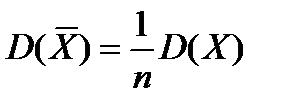 , т.е. дисперсия средней по выборке равна одной n-ой от дисперсии генеральной совокупности. Тогда для стандартного квадратичного отклонения
, т.е. дисперсия средней по выборке равна одной n-ой от дисперсии генеральной совокупности. Тогда для стандартного квадратичного отклонения 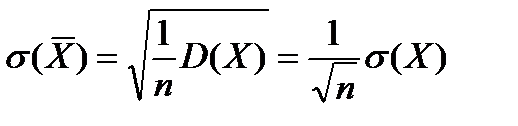 , где
, где 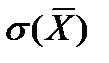 - стандартное квадратичное отклонение выборочного среднего, а
- стандартное квадратичное отклонение выборочного среднего, а 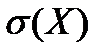 - стандартное квадратичное отклонение генеральной совокупности. Получилось, что при увеличении объёма выборки до n стандартное квадратичное отклонение выборочного среднего уменьшается в корень из n раз. Следовательно, для повышения эффективности выборочного среднего как оценки среднего генеральной совокупности нужно увеличивать объём выборки. Но при больших объёмах выборки большие увеличения выборки приводят к небольшому росту эффективности этой оценки, потому что стандартное квадратичное отклонение при этом уменьшается в корень квадратный из n раз.
- стандартное квадратичное отклонение генеральной совокупности. Получилось, что при увеличении объёма выборки до n стандартное квадратичное отклонение выборочного среднего уменьшается в корень из n раз. Следовательно, для повышения эффективности выборочного среднего как оценки среднего генеральной совокупности нужно увеличивать объём выборки. Но при больших объёмах выборки большие увеличения выборки приводят к небольшому росту эффективности этой оценки, потому что стандартное квадратичное отклонение при этом уменьшается в корень квадратный из n раз. и
и  , где, как и прежде, n – объём выборки, а N – это объём генеральной совокупности. В случае повторной выборки аналогичные формулы не зависели от объёма генеральной совокупности в силу случайности формирования такой выборки. Если объём генеральной совокупности бесконечен, очень велик или выборка составляет малую долю от генеральной совокупности, то отношение
, где, как и прежде, n – объём выборки, а N – это объём генеральной совокупности. В случае повторной выборки аналогичные формулы не зависели от объёма генеральной совокупности в силу случайности формирования такой выборки. Если объём генеральной совокупности бесконечен, очень велик или выборка составляет малую долю от генеральной совокупности, то отношение  будет очень мало или стремиться к нулю. В таком случае результаты вычисления дисперсии и стандартного квадратичного отклонения не будут отличаться от тех, которые получатся для повторной выборки.
будет очень мало или стремиться к нулю. В таком случае результаты вычисления дисперсии и стандартного квадратичного отклонения не будут отличаться от тех, которые получатся для повторной выборки.


