
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическая оценка вероятности или генеральной доли
Пусть генеральная совокупность содержит Генеральная доля непосредственно может быть определена в переписи генеральной совокупности. Оценка генеральной доли может быть дана по выборке из генеральной совокупности. Если построена выборка из Будем использовать ту же модель выборки, что и в предыдущих разделах. Пусть сделана выборка При определении выборочной доли в нашей модели Определим случайную величину Следовательно, математическое ожидание случайной величины Аналогично, дисперсия случайной величины Теперь можно определить математическое ожидание выборочной доли
Дисперсия выборочной доли Приведённые формулы справедливы для повторных выборок. Для бесповторных выборок в них необходимо вносить корректировки. В случае бесповторной выборки математическое ожидание выборочной доли совпадает с генеральной долей, как и в случае повторной выборки: В большинстве исследований используют именно бесповторные выборки, чтобы обеспечить в них большее разнообразие информации из генеральных совокупностей. Если объём выборки достаточно велик и при этом отношение объёма выборки к объёму генеральной совокупности Понятие интервальной оценки При статистическом оценивании параметров генеральной совокупности важно знать, в каких границах могут меняться их значения. Для того, чтобы ответить на такого рода вопросы, оказывается недостаточно знать только значения точечных оценок параметров генеральной совокупности по статистикам выборок. Для ответов на такие вопросы формируются так называемые интервальные оценки параметров генеральных совокупностей.
Интервальной оценкой параметра генеральной совокупности является интервал, внутри которого с высокой вероятностью находится истинное значение этого параметра. Часто такие интервалы строятся вокруг значений точечных оценок параметров генеральных совокупностей по статистикам выборок. Такие интервалы фактически показывают, насколько значения параметров генеральных совокупностей могут отличаться от точечных значений выборочных статистик.
|
||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 929; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.235.212 (0.008 с.) |
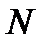 элементов, а из них
элементов, а из них 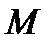 элементов обладают некоторым свойством. Тогда доля элементов в генеральной совокупности, обладающая этим свойством, равна
элементов обладают некоторым свойством. Тогда доля элементов в генеральной совокупности, обладающая этим свойством, равна 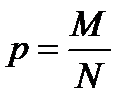 . Эту долю можно интерпретировать как вероятность того, что произвольно и случайно взятый из генеральной совокупности элемент будет обладать этим свойством. Величина
. Эту долю можно интерпретировать как вероятность того, что произвольно и случайно взятый из генеральной совокупности элемент будет обладать этим свойством. Величина 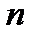 элементов, а в ней этим свойством обладает
элементов, а в ней этим свойством обладает  элементов, то доля элементов выборки, обладающих этим свойством, будет равна
элементов, то доля элементов выборки, обладающих этим свойством, будет равна  , которая называется выборочной долей или относительной частотой этого свойства в выборке. Можно доказать, что выборочная доля является несмещённой, состоятельной и эффективной оценкой генеральной доли для соответствующего свойства.
, которая называется выборочной долей или относительной частотой этого свойства в выборке. Можно доказать, что выборочная доля является несмещённой, состоятельной и эффективной оценкой генеральной доли для соответствующего свойства. из распределения
из распределения 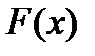 для случайной величины
для случайной величины  . Независимые измерения или наблюдения
. Независимые измерения или наблюдения 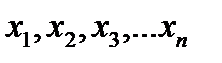 являются реализацией этой выборки.
являются реализацией этой выборки.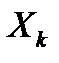 принимает значение 1, если реализация этой случайной величины
принимает значение 1, если реализация этой случайной величины  обладает исследуемым нами свойством элементов генеральной совокупности. Будем считать успехом то, что выбранный элемент обладает исследуемым свойством, а неудачей – что не обладает. Можно считать, что все
обладает исследуемым нами свойством элементов генеральной совокупности. Будем считать успехом то, что выбранный элемент обладает исследуемым свойством, а неудачей – что не обладает. Можно считать, что все  , а вероятностью неудачи
, а вероятностью неудачи 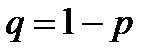 .
. , т.е. общее число успехов или общее число случаев, когда выбранные в реализацию выборки элементы обладают исследуемым свойством. Математическое ожидание отдельной случайной величины
, т.е. общее число успехов или общее число случаев, когда выбранные в реализацию выборки элементы обладают исследуемым свойством. Математическое ожидание отдельной случайной величины  . Тогда дисперсия этой случайной величины равна по определению:
. Тогда дисперсия этой случайной величины равна по определению: 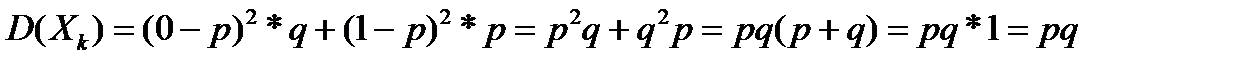 .
. равно:
равно: 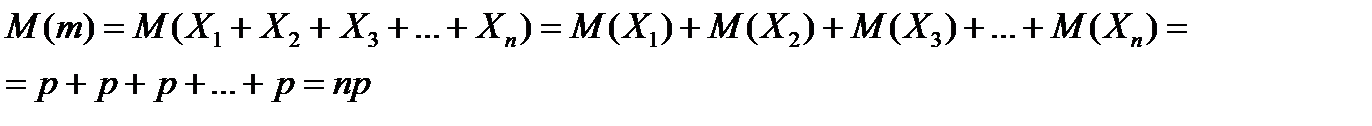
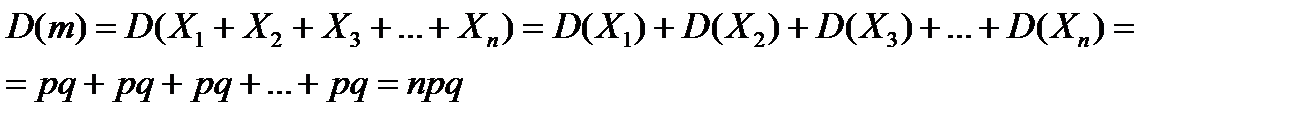
 является постоянной оно равно
является постоянной оно равно 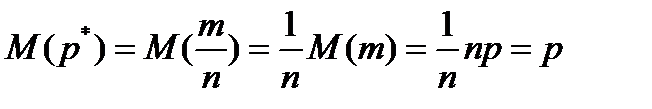 . Получилось, что математическое ожидание выборочной доли равно генеральной доле, т.е. выборочная доля является несмещённой оценкой генеральной доли. Можно доказать, что эта же оценка является эффективной и состоятельной.
. Получилось, что математическое ожидание выборочной доли равно генеральной доле, т.е. выборочная доля является несмещённой оценкой генеральной доли. Можно доказать, что эта же оценка является эффективной и состоятельной.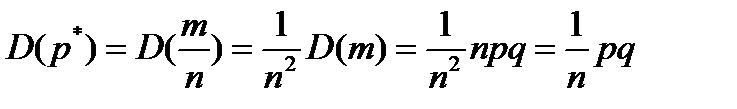 . Тогда стандартное квадратичное отклонение выборочной доли
. Тогда стандартное квадратичное отклонение выборочной доли  . Получается, что выборочная доля является тем более эффективной оценкой генеральной доли, чем больше размер выборки. Но рост точности оценивания происходит по квадратичному закону, т.е. при больших выборках приращение точности существенно меньше, чем при малых. Поэтому для оценивания долей или процентов в генеральных совокупностях очень дорого и трудно делать большие выборки. Они себя не оправдывают из-за невысокого роста точности оценивания. В современной социологии чаще всего используют выборки объёмов от 1500-1600 респондентов, до 2000 респондентов, а наибольшими на практике являются выборки в 4000 респондентов. При более высоких объёмах выборки существенно возрастают затраты денег и времени на проведение исследований, а приращение точности оценивания генеральных долей происходит незначительное. Такие исследования проводить экономически невыгодно.
. Получается, что выборочная доля является тем более эффективной оценкой генеральной доли, чем больше размер выборки. Но рост точности оценивания происходит по квадратичному закону, т.е. при больших выборках приращение точности существенно меньше, чем при малых. Поэтому для оценивания долей или процентов в генеральных совокупностях очень дорого и трудно делать большие выборки. Они себя не оправдывают из-за невысокого роста точности оценивания. В современной социологии чаще всего используют выборки объёмов от 1500-1600 респондентов, до 2000 респондентов, а наибольшими на практике являются выборки в 4000 респондентов. При более высоких объёмах выборки существенно возрастают затраты денег и времени на проведение исследований, а приращение точности оценивания генеральных долей происходит незначительное. Такие исследования проводить экономически невыгодно. . Но для вычисления дисперсии и стандартного квадратичного отклонения выборочной доли для бесповторной выборки необходимо сделать поправки:
. Но для вычисления дисперсии и стандартного квадратичного отклонения выборочной доли для бесповторной выборки необходимо сделать поправки: 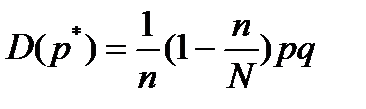 и
и  . Здесь
. Здесь  - объём выборки, а
- объём выборки, а  - объём генеральной совокупности.
- объём генеральной совокупности. мало, то закон распределения выборочной доли
мало, то закон распределения выборочной доли 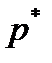 будет близок к нормальному. Это свойство выборочных долей часто используют в проведении практических исследований.
будет близок к нормальному. Это свойство выборочных долей часто используют в проведении практических исследований.


