
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Доверительный интервал для математического ожидания при неизвестном стандартном квадратичном отклонении
Пусть теперь остаётся неизвестным как значение математического ожидания некоторого параметра генеральной совокупности Как и ранее, предполагаем, что значения этого параметра в генеральной совокупности распределены по нормальному закону. Это не всегда легко проверить. Часто для проверки используются те или иные варианты законов больших чисел. Обычно, например, распределения, близкие к нормальным получаются в ситуациях действия многих относительно слабых и независимых факторов, которые могут определить значение этого параметра в генеральной совокупности. Напомним, что существует несмещённая оценка стандартного квадратичного отклонения значений рассматриваемого параметра генеральной совокупности, и такой оценкой является величина Построим новую случайную величину К распределению Стьюдента целесообразно перейти потому, что как доказывается оно не зависит от неизвестных нам параметров генеральной совокупности После определения
Таким образом, последовательность действий для определения доверительного интервала математического ожидания 1. Вычисляем несмещённую оценку стандартного квадратичного отклонения значений рассматриваемого параметра генеральной совокупности 2. По таблицам t-распределения Стьюдента или вычислениями в Microsoft Excel находим такое значение 3. Вычисляется половина доверительного интервала 4. Доверительный интервал записывается в виде На этом вычисление доверительного интервала при данных условиях заканчивается.
|
|||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 523; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.244.45 (0.005 с.) |
 , так и значение его дисперсии
, так и значение его дисперсии  в этой генеральной совокупности. Но, как и ранее, нам необходимо найти значение математического ожидания этого параметра генеральной совокупности
в этой генеральной совокупности. Но, как и ранее, нам необходимо найти значение математического ожидания этого параметра генеральной совокупности  .
. . Можно доказать, что эта случайная величина
. Можно доказать, что эта случайная величина 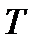 имеет распределение Стьюдента с
имеет распределение Стьюдента с 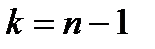 степенями свободы. Значения этой случайной величины будем обозначать через
степенями свободы. Значения этой случайной величины будем обозначать через  .
. и
и  . Тогда аналогично предыдущему можно решить уравнение
. Тогда аналогично предыдущему можно решить уравнение  . Решением этого уравнения является
. Решением этого уравнения является 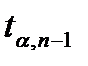 - значение аргумента функции распределения Стьюдента, для которого значение равно
- значение аргумента функции распределения Стьюдента, для которого значение равно  при числе степеней свободы
при числе степеней свободы  . Это значение аргумента
. Это значение аргумента  в расчётах интервальных оценок можно пользоваться функцией Лапласа вместо функции распределения Стьюдента для
в расчётах интервальных оценок можно пользоваться функцией Лапласа вместо функции распределения Стьюдента для  можно утверждать, что с доверительной вероятностью
можно утверждать, что с доверительной вероятностью  неизвестное значение средней параметра генеральной совокупности находится в доверительном интервале
неизвестное значение средней параметра генеральной совокупности находится в доверительном интервале 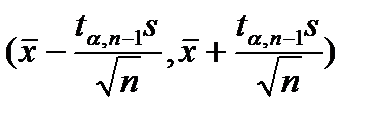 , т.е.
, т.е. 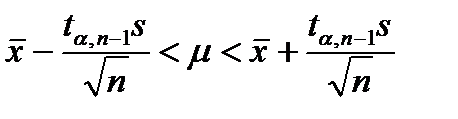 , где
, где  - это реализация средней в сделанной выборке из генеральной совокупности, а
- это реализация средней в сделанной выборке из генеральной совокупности, а 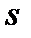 - это несмещённая оценка стандартного квадратичного отклонения значений рассматриваемого параметра генеральной совокупности, сделанная по этой выборке.
- это несмещённая оценка стандартного квадратичного отклонения значений рассматриваемого параметра генеральной совокупности, сделанная по этой выборке. должна быть следующей.
должна быть следующей. , для которого
, для которого  . Нужно использовать так называемую двустороннюю постановку вопроса, чтобы доверительная вероятность
. Нужно использовать так называемую двустороннюю постановку вопроса, чтобы доверительная вероятность 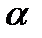 определяла ширину всего доверительного интервала, а не его половины. В случае t-распределения Стьюдента вычислять половину доверительной вероятности не следует.
определяла ширину всего доверительного интервала, а не его половины. В случае t-распределения Стьюдента вычислять половину доверительной вероятности не следует. по формуле
по формуле  .
. или
или 


