
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Доверительный интервал для математического ожидания при известном стандартном квадратичном отклонении
Известно значение дисперсии Предполагаем, что значения этого параметра в генеральной совокупности распределены по нормальному закону. Это не всегда легко проверить. Часто для проверки используются те или иные варианты законов больших чисел. Обычно, например, распределения, близкие к нормальным получаются в ситуациях действия многих относительно слабых и независимых факторов, которые могут определить значение этого параметра в генеральной совокупности. В большинстве случаев необходимо не то, что значения этого параметра в генеральной совокупности распределены по нормальному закону. Пусть сделана выборка Как мы уже выяснили, математическое ожидание выборочной средней равно математическому ожиданию или среднему значений в генеральной совокупности: Предположим, что мы задали доверительную вероятность
Напомним, что здесь У нас получилось, что
В результате получилось, что при заданном значении дисперсии Как видно, при возрастании объёма выборки точность такой интервальной оценки увеличивается, потому что значение Заметим, что эти формулы были получены для повторной выборки. Для бесповторной выборки логика вывода остаётся неизменной, но необходимо использовать дополнительный множитель в определении Таким образом, последовательность действий для определения доверительного интервала математического ожидания 1. Вычисляем значение половины доверительной вероятности
2. По таблицам функции Лапласа 3. Вычисляется половина доверительного интервала 4. Доверительный интервал записывается в виде На этом вычисление доверительного интервала при данных условиях заканчивается.
|
||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 641; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.70.137 (0.009 с.) |
 распределения некоторого параметра генеральной совокупности. Обозначим неизвестное нам значение математического ожидания этого параметра генеральной совокупности через
распределения некоторого параметра генеральной совокупности. Обозначим неизвестное нам значение математического ожидания этого параметра генеральной совокупности через  , интервальную оценку которого нам необходимо найти.
, интервальную оценку которого нам необходимо найти. из распределения
из распределения 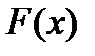 для случайной величины
для случайной величины  . Достаточно того, чтобы по нормальному закону были распределены значения выборочной средней
. Достаточно того, чтобы по нормальному закону были распределены значения выборочной средней  . Можно доказать, что при достаточно больших объёмах выборок (
. Можно доказать, что при достаточно больших объёмах выборок ( ) закон распределения выборочной средней будет близок к нормальному. Этот вывод обосновывается применением законов больших чисел.
) закон распределения выборочной средней будет близок к нормальному. Этот вывод обосновывается применением законов больших чисел.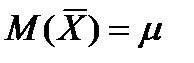 , а дисперсия выборочной средней будет
, а дисперсия выборочной средней будет 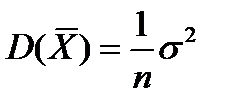 . Тогда стандартное квадратичное отклонение для
. Тогда стандартное квадратичное отклонение для  будет равно
будет равно  .
. , с которой значение среднего генеральной совокупности попадает в доверительный интервал, т.е. выполняется
, с которой значение среднего генеральной совокупности попадает в доверительный интервал, т.е. выполняется  . В этом соотношении
. В этом соотношении  нужно определить. Поскольку
нужно определить. Поскольку  является случайной величиной, распределённой по нормальному закону, для неё по свойствам функции распределения для нормального закона:
является случайной величиной, распределённой по нормальному закону, для неё по свойствам функции распределения для нормального закона:
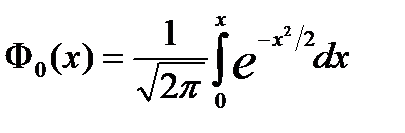 - это функция Лапласа, определяющая значения функции распределения стандартной нормальной случайной величины с математическим ожиданием или средней, равной 0, а дисперсией – 1.
- это функция Лапласа, определяющая значения функции распределения стандартной нормальной случайной величины с математическим ожиданием или средней, равной 0, а дисперсией – 1. . Из этого соотношения нужно найти
. Из этого соотношения нужно найти  . Если мы для удобства обозначим через
. Если мы для удобства обозначим через 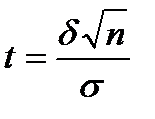 , то получим возможность выразить через
, то получим возможность выразить через  значение половины ширины доверительного интервала:
значение половины ширины доверительного интервала: 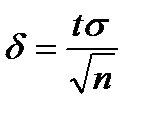 . А значение
. А значение  определяется из уравнения
определяется из уравнения  . На практике значение
. На практике значение 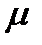 в генеральной совокупности находится внутри доверительного интервала
в генеральной совокупности находится внутри доверительного интервала  , т.е.
, т.е.  , где
, где  - это реализация средней в сделанной выборке из генеральной совокупности.
- это реализация средней в сделанной выборке из генеральной совокупности.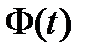 - это возрастающая функция, поэтому из уравнения
- это возрастающая функция, поэтому из уравнения 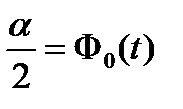 получается, что увеличение уровня доверительной вероятности приводит к увеличению значения
получается, что увеличение уровня доверительной вероятности приводит к увеличению значения 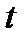 , а, следовательно, и
, а, следовательно, и  , где
, где  - это объём генеральной совокупности. Если
- это объём генеральной совокупности. Если 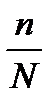 мало, например, когда объём генеральной совокупности
мало, например, когда объём генеральной совокупности  велик или бесповторная выборка имеет объём малый относительно объёма генеральной совокупности, множитель
велик или бесповторная выборка имеет объём малый относительно объёма генеральной совокупности, множитель  с высокой точностью равен 1, и им можно пренебречь. В этом случае для бесповторной выборки можно использовать те же формулы, что и для повторной без существенного снижения уровня точности определения ширины доверительного интервала.
с высокой точностью равен 1, и им можно пренебречь. В этом случае для бесповторной выборки можно использовать те же формулы, что и для повторной без существенного снижения уровня точности определения ширины доверительного интервала. должна быть следующей.
должна быть следующей. .
. или вычислениями в Microsoft Excel находим такое значение
или вычислениями в Microsoft Excel находим такое значение 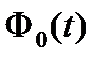 используют функцию
используют функцию  . В таких случаях для пересчёта значений нужно воспользоваться соотношением
. В таких случаях для пересчёта значений нужно воспользоваться соотношением  и тогда решать уравнение:
и тогда решать уравнение:  , т.е. искать такое значение
, т.е. искать такое значение  или записанное иначе
или записанное иначе 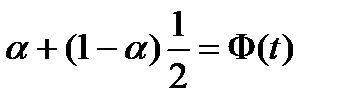 .
. по формуле
по формуле  или
или 


