Доверительный интервал для генеральной доли
Похожие статьи вашей тематики
Пусть генеральная совокупность содержит 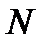 элементов, а из них элементов, а из них 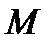 элементов обладают некоторым свойством. Тогда доля элементов в генеральной совокупности, обладающая этим свойством, равна элементов обладают некоторым свойством. Тогда доля элементов в генеральной совокупности, обладающая этим свойством, равна 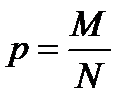 . Эту долю можно интерпретировать как вероятность того, что произвольно и случайно взятый из генеральной совокупности элемент будет обладать этим свойством. Величина . Эту долю можно интерпретировать как вероятность того, что произвольно и случайно взятый из генеральной совокупности элемент будет обладать этим свойством. Величина 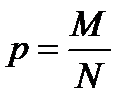 называется генеральной долей. называется генеральной долей.
Генеральная доля непосредственно может быть определена в переписи генеральной совокупности. Оценка генеральной доли может быть дана по выборке из генеральной совокупности.
Если построена выборка из 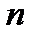 элементов, а в ней этим свойством обладает элементов, а в ней этим свойством обладает  элементов, то доля элементов выборки, обладающих этим свойством, будет равна элементов, то доля элементов выборки, обладающих этим свойством, будет равна  , которая называется выборочной долей или относительной частотой этого свойства в выборке. Можно доказать, что выборочная доля является несмещённой, состоятельной и эффективной оценкой генеральной доли для соответствующего свойства. , которая называется выборочной долей или относительной частотой этого свойства в выборке. Можно доказать, что выборочная доля является несмещённой, состоятельной и эффективной оценкой генеральной доли для соответствующего свойства.
Если объём выборки достаточно велик, а доля элементов в генеральной совокупности, обладающая рассматриваемым свойством 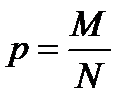 не очень мала, то можно считать, что случайная величина не очень мала, то можно считать, что случайная величина  распределена по нормальному закону. Поскольку мы ранее обосновали, что математическое ожидание выборочной доли равно генеральной доле, т.е. распределена по нормальному закону. Поскольку мы ранее обосновали, что математическое ожидание выборочной доли равно генеральной доле, т.е.  , то можно записать , то можно записать  , где , где 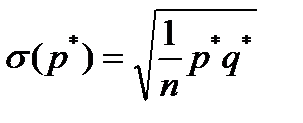 для повторной выборки и для повторной выборки и  для бесповторной выборки, а для бесповторной выборки, а  - это объём генеральной совокупности, - это объём генеральной совокупности,  - выборочная доля, а - выборочная доля, а  . .
Следовательно, из уравнения 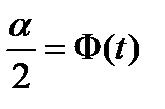 нужно определить значение нужно определить значение  , а потом значение половины ширины доверительного интервала из соотношения , а потом значение половины ширины доверительного интервала из соотношения  . Тогда эта половина доверительного интервала будет . Тогда эта половина доверительного интервала будет  . Получилось, что на уровне доверительной вероятности . Получилось, что на уровне доверительной вероятности  значение генеральной доли находится внутри доверительного интервала значение генеральной доли находится внутри доверительного интервала  , т.е. , т.е.  где где  вычисляется соответственно по формулам повторной или бесповторной выборок. вычисляется соответственно по формулам повторной или бесповторной выборок.
Таким образом, последовательность действий для определения доверительного интервала доли в генеральной совокупности по выборочной доле  с заданной доверительной вероятностью с заданной доверительной вероятностью  должна быть следующей. должна быть следующей.
1. Вычисляем долю отсутствия интересующего нас признака  . .
2. Вычисляем несмещённую оценку стандартного квадратичного отклонения 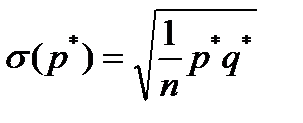 для повторной выборки или для повторной выборки или  для бесповторной выборки (этот вариант используется, когда объём выборки для бесповторной выборки (этот вариант используется, когда объём выборки 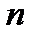 невелик). невелик).
3. Вычисляем значение половины доверительной вероятности  . .
4. По таблицам функции Лапласа  или вычислениями в Microsoft Excel находим такое значение или вычислениями в Microsoft Excel находим такое значение 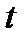 , для которого , для которого  . При вычислениях в Microsoft Excel, а иногда и при использовании статистических таблиц часто вместо функции Лапласа . При вычислениях в Microsoft Excel, а иногда и при использовании статистических таблиц часто вместо функции Лапласа 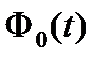 используют функцию используют функцию  . В таких случаях для пересчёта значений нужно воспользоваться соотношением . В таких случаях для пересчёта значений нужно воспользоваться соотношением  и тогда решать уравнение: и тогда решать уравнение:  , т.е. искать такое значение , т.е. искать такое значение 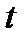 , для которого , для которого  или записанное иначе или записанное иначе 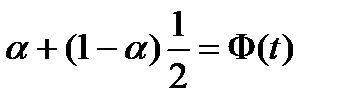 . .
5. Вычисляется половина доверительного интервала  по формуле по формуле  . .
6. Доверительный интервал записывается в виде 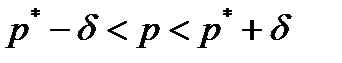 или или  . .
На этом вычисление доверительного интервала при данных условиях заканчивается.
|