
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка статистической гипотезы о генеральной доле
Пусть генеральная совокупность содержит Рассмотрим процедуру проверки статистической гипотезы о том, что генеральная доля равна какому-то наперёд заданному числу Если построена выборка из Можно доказать, что если объём выборки достаточно велик, в частности, превышает 500 элементов, выборочная доля Если нулевая гипотеза верна, то Вычисленное значение Пусть уровень значимости равен Случай 1. Альтернативная гипотеза представлена двусторонним неравенством
Критическая область для такой альтернативной гипотезы будет задаваться неравенством: Случай 2. Альтернативная гипотеза представлена односторонним неравенством Критическая область для такой альтернативной гипотезы будет задаваться неравенством: Случай 3. Альтернативная гипотеза представлена односторонним неравенством Критическая область для такой альтернативной гипотезы будет задаваться неравенством: Пример. В выборке из 1000 респондентов оказалось 200 голубоглазых. Известно, что в генеральной совокупности доля голубоглазых составляет 0,25. Можно ли на 95% уровне значимости утверждать, что сформированная выборка является репрезентативной по цвету глаз? Нулевой гипотезой будем считать равенство доли голубоглазых в генеральной совокупности и в выборке, а альтернативной двусторонней гипотезой – что эти доли не равны. Вычисляем значение критерия, т.е. Z-оценку в данном случае при объёме выборки
|
||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 815; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.1.100 (0.006 с.) |
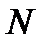 элементов, а из них
элементов, а из них 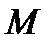 элементов обладают некоторым свойством. Тогда доля элементов в генеральной совокупности, обладающая этим свойством, равна
элементов обладают некоторым свойством. Тогда доля элементов в генеральной совокупности, обладающая этим свойством, равна 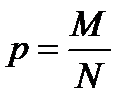 . Эту долю можно интерпретировать как вероятность того, что произвольно и случайно взятый из генеральной совокупности элемент будет обладать этим свойством. Величина
. Эту долю можно интерпретировать как вероятность того, что произвольно и случайно взятый из генеральной совокупности элемент будет обладать этим свойством. Величина  . Это означает, что ставится задача проверить нулевую гипотезу
. Это означает, что ставится задача проверить нулевую гипотезу  . В качестве альтернативной гипотезы можно выбрать следующие варианты:
. В качестве альтернативной гипотезы можно выбрать следующие варианты:  - двусторонняя,
- двусторонняя,  - односторонняя,
- односторонняя,  - тоже односторонняя.
- тоже односторонняя.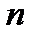 элементов, а в ней этим свойством обладает
элементов, а в ней этим свойством обладает  элементов, то доля элементов выборки, обладающих этим свойством, будет равна
элементов, то доля элементов выборки, обладающих этим свойством, будет равна  . Эта доля называется выборочной долей или относительной частотой этого свойства в выборке. Можно доказать, что выборочная доля является несмещённой, состоятельной и эффективной оценкой генеральной доли для соответствующего свойства.
. Эта доля называется выборочной долей или относительной частотой этого свойства в выборке. Можно доказать, что выборочная доля является несмещённой, состоятельной и эффективной оценкой генеральной доли для соответствующего свойства.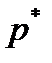 является случайной величиной, распределённой по закону, близкому к нормальному. В таком случае в качестве статистического критерия для проверки нулевой гипотезы можно использовать
является случайной величиной, распределённой по закону, близкому к нормальному. В таком случае в качестве статистического критерия для проверки нулевой гипотезы можно использовать  -оценку, имеющую стандартное нормальное распределение:
-оценку, имеющую стандартное нормальное распределение:  .
. . Следовательно,
. Следовательно,  . И тогда статистический критерий для проверки нулевой гипотезы получает такой вид:
. И тогда статистический критерий для проверки нулевой гипотезы получает такой вид:  .
.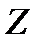 -оценки следует сравнить с критическим. А вывод о том, принимать или отклонять нулевую гипотезу определяется тем, как сформулированы альтернативные гипотезы.
-оценки следует сравнить с критическим. А вывод о том, принимать или отклонять нулевую гипотезу определяется тем, как сформулированы альтернативные гипотезы.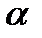 . Напомним, что уровень значимости задаёт исследователь из своих содержательных соображений, используя свой опыт проверки аналогичных гипотез. По таблицам или, например, в Excel необходимо определить значение
. Напомним, что уровень значимости задаёт исследователь из своих содержательных соображений, используя свой опыт проверки аналогичных гипотез. По таблицам или, например, в Excel необходимо определить значение  - границу критической области. Это значение аргумента, при котором стандартная нормальная величина принимает значение
- границу критической области. Это значение аргумента, при котором стандартная нормальная величина принимает значение  (двусторонняя гипотеза).
(двусторонняя гипотеза). . Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия
. Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия  попадает в критическую область.
попадает в критическую область. (односторонняя гипотеза).
(односторонняя гипотеза). . Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия
. Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия  . Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия
. Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия  , доле голубоглазых в генеральной совокупности
, доле голубоглазых в генеральной совокупности  и их доле в выборке
и их доле в выборке  :
:  . При этом по таблицам или в Microsoft Excel, используя функцию =НОРМСТОБР, можно найти критическое значение этого критерия для уровня значимости 0,95. Это критическое значение равно 1,6449, оно существенно меньше по модулю, чем вычисленное значение критерия для сравнения долей голубоглазых в генеральной совокупности и в выборке. Поэтому нет оснований принимать нулевую гипотезу, получается, что она должна быть отвергнута, и на уровне значимости 0,95 эти доли существенно различаются.
. При этом по таблицам или в Microsoft Excel, используя функцию =НОРМСТОБР, можно найти критическое значение этого критерия для уровня значимости 0,95. Это критическое значение равно 1,6449, оно существенно меньше по модулю, чем вычисленное значение критерия для сравнения долей голубоглазых в генеральной совокупности и в выборке. Поэтому нет оснований принимать нулевую гипотезу, получается, что она должна быть отвергнута, и на уровне значимости 0,95 эти доли существенно различаются.


