
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка статистической гипотезы о равенстве долей или вероятностей
Пусть в двух генеральных совокупностях проводятся независимые испытания, в результате которых может осуществиться или не осуществиться одно и то же событие. Обозначим неизвестную долю появления этого события в первой генеральной совокупности через Для осуществления проверки нулевой гипотезы производится выборка, объёмом Если обе выборки достаточно велики, то законы распределения случайных величин Выше уже обосновывалось, что математическое ожидание выборочной частоты равно генеральной доле: Покажем, что Если нулевая гипотеза верна, то Для проверки нулевой гипотезы в этом случае используют Вычисленное значение Пусть уровень значимости равен
Случай 1. Альтернативная гипотеза представлена двусторонним неравенством Критическая область для такой альтернативной гипотезы будет задаваться неравенством: Случай 2. Альтернативная гипотеза представлена односторонним неравенством Критическая область для такой альтернативной гипотезы будет задаваться неравенством: Случай 3. Альтернативная гипотеза представлена односторонним неравенством Критическая область для такой альтернативной гипотезы будет задаваться неравенством: Пример. Для того чтобы оценить в сравнении активность электората Москвы и Санкт-Петербурга при избрании депутатов Государственной Думы, была сделана случайная выборка избирателей в этих двух городах. Затем выяснялось, какая часть каждой выборки реально пришла на тот или иной избирательный участок для участия в выборах. Данные оказались следующими: в Москве из 1500 потенциальных случайно выбранных избирателей реально в выборах приняли участие 480 человек, а в Санкт-Петербурге из 1630 потенциальных избирателей на избирательные участки пришли 490 человек. На уровне значимости 10% проверить гипотезу о равенстве генеральных долей избирателей в двух этих городах, которые реально приняли участие в выборах.
В качестве нулевой гипотезы можно принять равенство генеральных долей избирателей в Москве и в Санкт-Петербурге, а в качестве двусторонней альтернативной гипотезы – неравенство этих долей. В данном случае в Москве приняли участие в выборах Вычислим наилучшую точечную статистическую оценку доли, если она одинакова в обоих генеральных совокупностях: По таблице значений функции Лапласа или используя функцию =НОРМСТОБР в Microsoft Excel находим критические значения для нормального распределения: для уровня значимости 0,9 оно равно 1,2816, а дополнительно – для уровня значимости 0,95 оно равно 1,6449, для уровня значимости 0,99 оно равно 2,3263. Для всех уровней значимости получается, что вычисленное значение Z-оценки оказалось меньшим критических при указанных выше уровнях значимости – 0,9, 0,95 и 0,99. Ъто означает, что вычисленное значение Z-оценки находится в области допустимых значений, поэтому нет оснований отвергать нулевую гипотезу. Следовательно, генеральные доли избирателей, реально принявших участие в выборах в Москве и в Санкт-Петербурге, статистически значимо не отличаются, т.е. их можно считать одинаковыми. Покажем все найденные значения на графике плотности стандартного нормального закона распределения, который описывает поведение случайной величины Zпри справедливости нулевой гипотезы.
График стандартного нормального распределения с указанием области допустимых и критических значений для уровня значимости 0,9 ( На этом графике видно, что красная точка, соответствующая вычисленному значению Z-оценки, находится внутри области допустимых значений нулевой гипотезы на уровне значимости 0,9. Это положение красной точки и определяет вывод о том, что нет оснований отвергать нулевую гипотезу на этом уровне значимости.
|
|||||||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 2864; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.155.139 (0.01 с.) |
 , а во второй генеральной совокупности – через
, а во второй генеральной совокупности – через 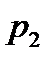 . Нулевая гипотеза формулируется как утверждение о равенстве этих долей в обоих генеральных совокупностях:
. Нулевая гипотеза формулируется как утверждение о равенстве этих долей в обоих генеральных совокупностях:  , где
, где  - это просто обозначение общего значения долей в двух генеральных совокупностях. В качестве альтернативной гипотезы можно выбрать следующие варианты:
- это просто обозначение общего значения долей в двух генеральных совокупностях. В качестве альтернативной гипотезы можно выбрать следующие варианты:  - двусторонняя,
- двусторонняя, 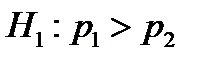 - односторонняя,
- односторонняя,  - тоже односторонняя.
- тоже односторонняя. из первой генеральной совокупности, т.е. для этой генеральной совокупности произведено
из первой генеральной совокупности, т.е. для этой генеральной совокупности произведено  испытаний. Пусть в этих испытаниях интересующее нас событие появлялось
испытаний. Пусть в этих испытаниях интересующее нас событие появлялось 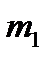 раз. Тогда относительная частота появления этого события в выборке из первой генеральной совокупности
раз. Тогда относительная частота появления этого события в выборке из первой генеральной совокупности 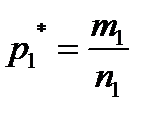 . Аналогично, производится выборка, объёмом
. Аналогично, производится выборка, объёмом  из второй генеральной совокупности, т.е. для этой генеральной совокупности произведено
из второй генеральной совокупности, т.е. для этой генеральной совокупности произведено  испытаний. Пусть в этих испытаниях интересующее нас событие появлялось
испытаний. Пусть в этих испытаниях интересующее нас событие появлялось  раз. Тогда относительная частота появления этого события в выборке из второй генеральной совокупности
раз. Тогда относительная частота появления этого события в выборке из второй генеральной совокупности 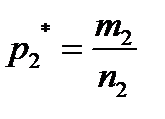 .
.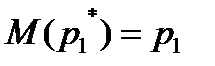 и
и  . Дисперсии этих случайных величин таковы:
. Дисперсии этих случайных величин таковы:  и
и  .
. является несмещённой оценкой для
является несмещённой оценкой для  . Действительно,
. Действительно,  . Поскольку испытания независимы, выборки будут тоже независимыми. Тогда можно использовать следующую формулу для дисперсии разности:
. Поскольку испытания независимы, выборки будут тоже независимыми. Тогда можно использовать следующую формулу для дисперсии разности:  .
. . Величина
. Величина  .
. -оценку, имеющую стандартное нормальное распределение:
-оценку, имеющую стандартное нормальное распределение: 
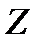 -оценки следует сравнить с критическим. А вывод о том, принимать или отклонять нулевую гипотезу определяется тем, как сформулированы альтернативные гипотезы.
-оценки следует сравнить с критическим. А вывод о том, принимать или отклонять нулевую гипотезу определяется тем, как сформулированы альтернативные гипотезы.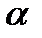 . Напомним, что уровень значимости задаёт исследователь из своих содержательных соображений, используя свой опыт проверки аналогичных гипотез. По таблицам или, например, в Excel необходимо определить значение
. Напомним, что уровень значимости задаёт исследователь из своих содержательных соображений, используя свой опыт проверки аналогичных гипотез. По таблицам или, например, в Excel необходимо определить значение  - границу критической области. Это значение аргумента, при котором стандартная нормальная величина принимает значение
- границу критической области. Это значение аргумента, при котором стандартная нормальная величина принимает значение  . Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия
. Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия  попадает в критическую область.
попадает в критическую область. . Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия
. Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия  . Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия
. Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия 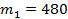 человек из
человек из  избирателей, а в Санкт-Петербурге –
избирателей, а в Санкт-Петербурге – 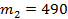 человек из
человек из  избирателей. Тогда доли избирателей из выборок, реально принявших участие в выборах в Москве равна
избирателей. Тогда доли избирателей из выборок, реально принявших участие в выборах в Москве равна  , а в Санкт-Петербурге –
, а в Санкт-Петербурге – 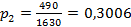 .
. . Используя эту оценку доли избирателей, вычислим Z-оценку:
. Используя эту оценку доли избирателей, вычислим Z-оценку: 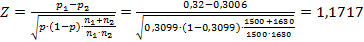 .
.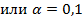 ). Тогда
). Тогда 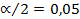 , а
, а 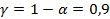 ).
).


