
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка статистической гипотезы о равенстве средних
Пусть По независимым выборкам из Требуется по выборочным средним при заданном уровне значимости
Как известно, выборочные средние являются несмещёнными оценками генеральных средних или математических ожиданий, т.е.
В качестве статистического критерия для проверки этих гипотез можно использовать случайную величину -
Тогда можно доказать, что
Для доказательства преобразуем Этот статистический критерий имеет стандартное нормальное распределение. Критическая область этого критерия определяется в зависимости от альтернативной гипотезы. Случай 1. Альтернативная гипотеза представлена двусторонним неравенством Пусть уровень значимости равен Критическая область для такой альтернативной гипотезы будет задаваться неравенством: Случай 2. Альтернативная гипотеза представлена односторонним неравенством
Пусть уровень значимости равен Критическая область для такой альтернативной гипотезы будет задаваться неравенством: Случай 3. Альтернативная гипотеза представлена односторонним неравенством Пусть уровень значимости равен Критическая область для такой альтернативной гипотезы будет задаваться неравенством: Если дисперсии генеральных совокупностей Одно их таких приближений такое. Можно доказать, что в случае объёмов выборок из
и
Дальнейшая процедура проверки статистической гипотезы не меняется, она полностью повторяет ту, которая была описана для случая известных дисперсий генеральных совокупностей. Пример. Была измерена скорость чтения у детей. До обучения чтению по некоторой методике средняя скорость чтения составляла 100 слов в минуту со стандартным отклонением 12 для 100 обследованных детей. После обучения чтению по этой методике только 81 ребенка их скорость чтения в среднем составила 130 слов в минуту при стандартном отклонении 14. Можно ли на основании применения того или иного статистического критерия утверждать, есть эффект обучения детей чтению или нет? Нулевой гипотезой будем считать отсутствие существенных различий в скоростях чтения до и после обучения, а альтернативной гипотезой – наличие таких отличий. Таким образом, мы проверяем двустороннюю гипотезу. В данном случае можно применить критерий сравнения средних по Z-оценке, т.е. считая, что данные имеют близкие к нормальным распределения и до обучения, и после обучения чтению. В этом случае: распределение X – это распределение скоростей чтения до обучения, распределение Y – это распределение скоростей чтения после обучения по методике, Вычисляем значение статистического критерия
|
||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 499; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.0.88 (0.012 с.) |
 и
и  - две случайные величины, распределённые обе по нормальному закону с неизвестными математическими ожиданиями и известными дисперсиями
- две случайные величины, распределённые обе по нормальному закону с неизвестными математическими ожиданиями и известными дисперсиями  и
и  соответственно. Процедуры и выводы этого раздела можно применять и в тех случаях, когда случайные величины
соответственно. Процедуры и выводы этого раздела можно применять и в тех случаях, когда случайные величины 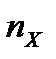 и
и  , определены выборочные средние
, определены выборочные средние  и
и  .
. проверить нулевую гипотезу, состоящую в том, что математические ожидания генеральных совокупностей
проверить нулевую гипотезу, состоящую в том, что математические ожидания генеральных совокупностей  - нулевая гипотеза;
- нулевая гипотеза; ,
,  или
или  - альтернативные гипотезы.
- альтернативные гипотезы. и
и  , где
, где  и
и  - это случайные величины, являющиеся выборочными средними для
- это случайные величины, являющиеся выборочными средними для 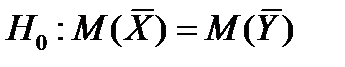 - нулевая гипотеза;
- нулевая гипотеза; ,
,  или
или  - альтернативные гипотезы.
- альтернативные гипотезы.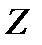 - оценку следующего вида:
- оценку следующего вида: .
.
 . Но выборочная дисперсия может быть выражена через дисперсию генеральной совокупности:
. Но выборочная дисперсия может быть выражена через дисперсию генеральной совокупности:  Аналогично:
Аналогично:  . Следовательно,
. Следовательно,  . Тогда статистический критерий и принимает вид:
. Тогда статистический критерий и принимает вид: 
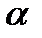 . По таблицам или, например, в Excel необходимо определить значение
. По таблицам или, например, в Excel необходимо определить значение  - границу критической области. Это значение аргумента, при котором стандартная нормальная величина принимает значение
- границу критической области. Это значение аргумента, при котором стандартная нормальная величина принимает значение  . Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия
. Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия  попадает в критическую область.
попадает в критическую область. . Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия
. Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия  . Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия
. Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия  , где
, где  и
и 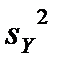 - это несмещённые выборочные оценки дисперсии генеральных совокупностей
- это несмещённые выборочные оценки дисперсии генеральных совокупностей 

 – это средняя скорость чтения до обучения,
– это средняя скорость чтения до обучения,  – это средняя скорость чтения после обучения по методике,
– это средняя скорость чтения после обучения по методике,  – это дисперсия распределения X,
– это дисперсия распределения X,  – это дисперсия распределения Y,
– это дисперсия распределения Y,  – это размер выборки до обучения чтению, а
– это размер выборки до обучения чтению, а  – это размер выборки после обучения чтению по методике.
– это размер выборки после обучения чтению по методике. . По таблицам или с помощью функции =НОРМСТОБР в Microsoft Excel вычисляем критические значения для этого критерия на уровнях значимости 0,95 и 0,99. Получаются, соответственно, критические значения 1,6449 и 2,3263. Значение статистического критерия, вычисленного для сравнения скоростей чтения до и после обучения по модулю существенно больше и одного и другого критического значения. Следовательно, наше значение статистического критерия, показывающее различия в скоростях чтения, лежит вне области допустимых значения критерия. Поэтому нулевая гипотеза должна быть отвергнута на обоих уровнях значимости, что означает статистическое подтверждение наличия эффекта обучения чтению по применённой методике обучения.
. По таблицам или с помощью функции =НОРМСТОБР в Microsoft Excel вычисляем критические значения для этого критерия на уровнях значимости 0,95 и 0,99. Получаются, соответственно, критические значения 1,6449 и 2,3263. Значение статистического критерия, вычисленного для сравнения скоростей чтения до и после обучения по модулю существенно больше и одного и другого критического значения. Следовательно, наше значение статистического критерия, показывающее различия в скоростях чтения, лежит вне области допустимых значения критерия. Поэтому нулевая гипотеза должна быть отвергнута на обоих уровнях значимости, что означает статистическое подтверждение наличия эффекта обучения чтению по применённой методике обучения.


