Пусть  - случайная величина, распределённая по нормальному закону с математическим ожиданием
- случайная величина, распределённая по нормальному закону с математическим ожиданием  и дисперсией
и дисперсией  . Процедуры и выводы этого раздела можно применять и в тех случаях, когда случайная величина
. Процедуры и выводы этого раздела можно применять и в тех случаях, когда случайная величина  распределена не точно по нормальному закону, но близко к нему.
распределена не точно по нормальному закону, но близко к нему.
Сначала рассмотрим случай, когда математическое ожидание  этой случайной величины
этой случайной величины  неизвестно и его необходимо определить, но дисперсия
неизвестно и его необходимо определить, но дисперсия  этой случайной величины известна.
этой случайной величины известна.
Типичная статистическая гипотеза в этом случае может быть сформулирована так:  , где
, где  - предполагаемое значение математического ожидания. Альтернативные гипотезы для этой нулевой могут быть трёх разных вариантов:
- предполагаемое значение математического ожидания. Альтернативные гипотезы для этой нулевой могут быть трёх разных вариантов:  (двусторонняя гипотеза),
(двусторонняя гипотеза),  (левосторонняя гипотеза) или
(левосторонняя гипотеза) или  (правосторонняя гипотеза). Неравенства в односторонних гипотезах можно заменять нестрогими, результаты проверки от этого не изменятся, потому что вероятность принять какое-то конкретное значение для нормальной случайной величины равна нулю.
(правосторонняя гипотеза). Неравенства в односторонних гипотезах можно заменять нестрогими, результаты проверки от этого не изменятся, потому что вероятность принять какое-то конкретное значение для нормальной случайной величины равна нулю.
В предположении, что дисперсия  случайной величины
случайной величины  известна, в качестве статистического критерия можно использовать
известна, в качестве статистического критерия можно использовать 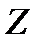 -оценку:
-оценку:  , где
, где  - средняя по выборке,
- средняя по выборке,  - предполагаемое значение средней по генеральной совокупности,
- предполагаемое значение средней по генеральной совокупности,  - стандартное квадратичное отклонение в генеральной совокупности,
- стандартное квадратичное отклонение в генеральной совокупности,  - объём выборки. Вычисленное значение
- объём выборки. Вычисленное значение 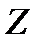 -оценки следует сравнить с критическим. А вывод о том, принимать или отклонять нулевую гипотезу определяется тем, как сформулированы альтернативные гипотезы.
-оценки следует сравнить с критическим. А вывод о том, принимать или отклонять нулевую гипотезу определяется тем, как сформулированы альтернативные гипотезы.
Случай 1. Альтернативная гипотеза представлена двусторонним неравенством  (двусторонняя гипотеза).
(двусторонняя гипотеза).
Пусть уровень значимости равен 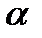 . По таблицам или, например, в Excel необходимо определить значение
. По таблицам или, например, в Excel необходимо определить значение  - границу критической области. Это значение аргумента, при котором стандартная нормальная величина принимает значение
- границу критической области. Это значение аргумента, при котором стандартная нормальная величина принимает значение 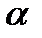 .
.
Критическая область для такой альтернативной гипотезы будет задаваться неравенством:  . Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия
. Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия  попадает в критическую область.
попадает в критическую область.
Случай 2. Альтернативная гипотеза представлена односторонним неравенством  (односторонняя гипотеза).
(односторонняя гипотеза).
Пусть уровень значимости равен 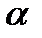 . По таблицам или, например, в Excel необходимо определить значение
. По таблицам или, например, в Excel необходимо определить значение  - границу критической области. Это значение аргумента, при котором стандартная нормальная величина принимает значение
- границу критической области. Это значение аргумента, при котором стандартная нормальная величина принимает значение 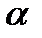 .
.
Критическая область для такой альтернативной гипотезы будет задаваться неравенством:  . Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия
. Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия  попадает в критическую область.
попадает в критическую область.
Случай 3. Альтернативная гипотеза представлена односторонним неравенством  (односторонняя гипотеза).
(односторонняя гипотеза).
Пусть уровень значимости равен 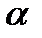 . По таблицам или, например, в Excel необходимо определить значение
. По таблицам или, например, в Excel необходимо определить значение  - границу критической области. Это значение аргумента, при котором стандартная нормальная величина принимает значение
- границу критической области. Это значение аргумента, при котором стандартная нормальная величина принимает значение 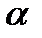 .
.
Критическая область для такой альтернативной гипотезы будет задаваться неравенством:  . Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия
. Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия  попадает в критическую область.
попадает в критическую область.
В предположении, что дисперсия  случайной величины
случайной величины  неизвестна, в качестве статистического критерия можно использовать
неизвестна, в качестве статистического критерия можно использовать  -распределение Стьюдента:
-распределение Стьюдента:  , где
, где  - средняя по выборке,
- средняя по выборке,  - предполагаемое значение средней по генеральной совокупности,
- предполагаемое значение средней по генеральной совокупности,  - стандартное квадратичное отклонение в выборке, определённое с учётом поправки на несмещённость,
- стандартное квадратичное отклонение в выборке, определённое с учётом поправки на несмещённость,  - объём выборки. В таком случае число степеней свободы, от которого зависят значения
- объём выборки. В таком случае число степеней свободы, от которого зависят значения  -распределения Стьюдента, будет равно
-распределения Стьюдента, будет равно  . Вычисленное значение
. Вычисленное значение  следует сравнить с критическим
следует сравнить с критическим 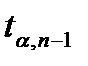 , определяемым как аргумент функции распределения
, определяемым как аргумент функции распределения  -распределения Стьюдента, при котором значение этой функции распределения равно уровню значимости
-распределения Стьюдента, при котором значение этой функции распределения равно уровню значимости 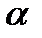 . А вывод о том, принимать или отклонять нулевую гипотезу определяется тем, как сформулированы альтернативные гипотезы.
. А вывод о том, принимать или отклонять нулевую гипотезу определяется тем, как сформулированы альтернативные гипотезы.
Случай 1. Альтернативная гипотеза представлена двусторонним неравенством  (двусторонняя гипотеза). Критическая область для такой альтернативной гипотезы будет задаваться неравенством:
(двусторонняя гипотеза). Критическая область для такой альтернативной гипотезы будет задаваться неравенством: 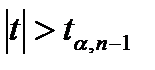 . Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия
. Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия  попадает в критическую область.
попадает в критическую область.
Случай 2. Альтернативная гипотеза представлена односторонним неравенством  (односторонняя гипотеза). Критическая область для такой альтернативной гипотезы будет задаваться неравенством:
(односторонняя гипотеза). Критическая область для такой альтернативной гипотезы будет задаваться неравенством: 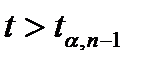 . Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия
. Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия 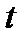 попадает в критическую область.
попадает в критическую область.
Случай 3. Альтернативная гипотеза представлена односторонним неравенством  (односторонняя гипотеза). Критическая область для такой альтернативной гипотезы будет задаваться неравенством:
(односторонняя гипотеза). Критическая область для такой альтернативной гипотезы будет задаваться неравенством:  . Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия
. Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия 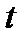 попадает в критическую область.
попадает в критическую область.
Пример. Владелец небольшого магазина утверждает, что среднедневная выручка за прошлый год у него составила 35000 рублей. Для проверки были выбраны 40 дней этого года, по которым среднедневная выручка составила 33500 рублей при стандартном отклонении 3500 рублей. Можно ли на уровне значимости 0,95 доверять утверждению владельца магазина о его среднедневной выручке за прошлый год? А на уровне значимости 0,99?
В данном случае нулевой гипотезой будем считать равенство среднедневных выручек по данным владельца магазина и по данным выборочной проверки. Альтернативной гипотезой будем считать неравенство этих средних. Поскольку нам известно стандартное отклонение только для выборочной проверки, в качестве статистического критерия необходимо использовать  -распределение Стьюдента.
-распределение Стьюдента.
Вычисляем значение  -распределения Стьюдента при средней по генеральной совокупности
-распределения Стьюдента при средней по генеральной совокупности  , среднем по выборке
, среднем по выборке  , стандартном отклонении по выборке
, стандартном отклонении по выборке  , объёме выборки
, объёме выборки 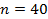 , а потому числе степеней свободы
, а потому числе степеней свободы  :
:  .
.
Для уровня значимости 0,95 и числе степеней свободы 39 определяем критическое значение  -распределения Стьюдента, оно равно 2,0227. При этом для расчётов в Microsoft Excel необходимо использовать функцию =СТЬЮДРАСПОБР, а в качестве уровня значимости его американское значение
-распределения Стьюдента, оно равно 2,0227. При этом для расчётов в Microsoft Excel необходимо использовать функцию =СТЬЮДРАСПОБР, а в качестве уровня значимости его американское значение 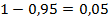 . В нашем случае получается, что вычисленное значение
. В нашем случае получается, что вычисленное значение  -распределения Стьюдента лежит вне области допустимых значений, потому что 2,7105>2,0227. Следовательно, на уровне значимости 0,95 нулевая гипотеза отвергается, и владелец магазина занизил среднедневную выручку за прошлый год. Аналогично, на уровне значимости 0,99 критическое значение
-распределения Стьюдента лежит вне области допустимых значений, потому что 2,7105>2,0227. Следовательно, на уровне значимости 0,95 нулевая гипотеза отвергается, и владелец магазина занизил среднедневную выручку за прошлый год. Аналогично, на уровне значимости 0,99 критическое значение  -распределения Стьюдента будет равно 2,7079. И на этом, более высоком уровне значимости вычисленное значение
-распределения Стьюдента будет равно 2,7079. И на этом, более высоком уровне значимости вычисленное значение  -распределения Стьюдента лежит вне области допустимых значений, потому что 2,7105>2,7079. Следовательно, с ещё большей достоверностью, можно утверждать, что владелец магазина занизил среднедневную выручку за прошлый год.
-распределения Стьюдента лежит вне области допустимых значений, потому что 2,7105>2,7079. Следовательно, с ещё большей достоверностью, можно утверждать, что владелец магазина занизил среднедневную выручку за прошлый год.


 - случайная величина, распределённая по нормальному закону с математическим ожиданием
- случайная величина, распределённая по нормальному закону с математическим ожиданием  и дисперсией
и дисперсией  . Процедуры и выводы этого раздела можно применять и в тех случаях, когда случайная величина
. Процедуры и выводы этого раздела можно применять и в тех случаях, когда случайная величина  , где
, где  - предполагаемое значение математического ожидания. Альтернативные гипотезы для этой нулевой могут быть трёх разных вариантов:
- предполагаемое значение математического ожидания. Альтернативные гипотезы для этой нулевой могут быть трёх разных вариантов:  (двусторонняя гипотеза),
(двусторонняя гипотеза),  (левосторонняя гипотеза) или
(левосторонняя гипотеза) или  (правосторонняя гипотеза). Неравенства в односторонних гипотезах можно заменять нестрогими, результаты проверки от этого не изменятся, потому что вероятность принять какое-то конкретное значение для нормальной случайной величины равна нулю.
(правосторонняя гипотеза). Неравенства в односторонних гипотезах можно заменять нестрогими, результаты проверки от этого не изменятся, потому что вероятность принять какое-то конкретное значение для нормальной случайной величины равна нулю.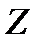 -оценку:
-оценку:  , где
, где  - средняя по выборке,
- средняя по выборке,  - предполагаемое значение средней по генеральной совокупности,
- предполагаемое значение средней по генеральной совокупности,  - стандартное квадратичное отклонение в генеральной совокупности,
- стандартное квадратичное отклонение в генеральной совокупности,  - объём выборки. Вычисленное значение
- объём выборки. Вычисленное значение 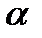 . По таблицам или, например, в Excel необходимо определить значение
. По таблицам или, например, в Excel необходимо определить значение  - границу критической области. Это значение аргумента, при котором стандартная нормальная величина принимает значение
- границу критической области. Это значение аргумента, при котором стандартная нормальная величина принимает значение  . Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия
. Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия  попадает в критическую область.
попадает в критическую область. (односторонняя гипотеза).
(односторонняя гипотеза). . Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия
. Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия  (односторонняя гипотеза).
(односторонняя гипотеза). . Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия
. Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия  -распределение Стьюдента:
-распределение Стьюдента:  , где
, где  - стандартное квадратичное отклонение в выборке, определённое с учётом поправки на несмещённость,
- стандартное квадратичное отклонение в выборке, определённое с учётом поправки на несмещённость,  . Вычисленное значение
. Вычисленное значение  следует сравнить с критическим
следует сравнить с критическим 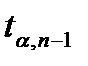 , определяемым как аргумент функции распределения
, определяемым как аргумент функции распределения 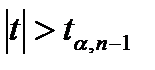 . Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия
. Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия  попадает в критическую область.
попадает в критическую область. (односторонняя гипотеза). Критическая область для такой альтернативной гипотезы будет задаваться неравенством:
(односторонняя гипотеза). Критическая область для такой альтернативной гипотезы будет задаваться неравенством: 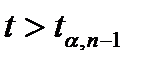 . Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия
. Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия 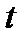 попадает в критическую область.
попадает в критическую область. (односторонняя гипотеза). Критическая область для такой альтернативной гипотезы будет задаваться неравенством:
(односторонняя гипотеза). Критическая область для такой альтернативной гипотезы будет задаваться неравенством:  . Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия
. Если это неравенство выполняется, нет оснований принимать нулевую гипотезу, т.е. она должна быть отклонена, поскольку значение статистического критерия  , среднем по выборке
, среднем по выборке  , стандартном отклонении по выборке
, стандартном отклонении по выборке  , объёме выборки
, объёме выборки 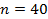 , а потому числе степеней свободы
, а потому числе степеней свободы  :
:  .
.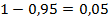 . В нашем случае получается, что вычисленное значение
. В нашем случае получается, что вычисленное значение 


