
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основной принцип проверки статистической гипотезы
Основной принцип проверки статистической гипотезы следующий. Сначала нужно сформулировать нулевую гипотезу Проверка статистической гипотезы сводится к принятию решения, следует ли принять нулевую гипотезу или отклонить ее в пользу альтернативной. При этом нулевая гипотеза (постулирующая отсутствие различий) выступает в качестве утверждения, которое считается справедливым до тех пор, пока не будут найдены противоречащие ему факты. При проверке статистических критериев с той или иной вероятностью могут совершаться ошибки. Ошибкой первого рода называется такая, при совершении которой в результате проверки отвергают правильную статистическую гипотезу. Вероятность ошибки первого рода называется уровнем значимости, обычно его обозначают буквой Ошибкой второго рода называется такая, при совершении которой в результате проверки принимается нулевая гипотеза в ситуации, когда она неверна. Вероятность ошибки второго рода обычно обозначается буквой
Нулевая и альтернативная гипотезы принимаются на основе одного и того же правила, которое называется критерием нулевой гипотезы. Однако условия их принятия принципиально асимметричны. Альтернативная гипотеза принимается в том случае, когда нулевая не подтверждается и должна быть отклонена. Решение о принятии альтернативной гипотезы происходит при зафиксированном значении вероятности ошибки первого рода α. Нулевая гипотеза принимается во всех случаях, когда ее нельзя отклонить. Однако при принятии нулевой гипотезы необходимо оценивать вероятность правильности такого решения (1 - β), которая называется мощностью критерия. Критерий нулевой гипотезы строится на основе специально подобранной численной функции, которая вычисляется по выборке и называется статистикой критерия.
Геометрическая иллюстрация областей принятия и отклонения нулевой гипотезы
Рис.1. Области принятия и отклонения нулевой гипотезы.
Предположим, что истинное значение оцениваемого параметра
Целесообразно полагать одинаковыми значения вероятности выхода параметра Если предположить, что истинное значение параметра в действительности сдвинуто и равно
Рис.2. Что происходит при сдвиге реального значения статистического критерия.
При заданном объеме выборки вероятность совершения ошибки первого рода можно уменьшить, снижая уровень значимости Единственный способ уменьшить обе вероятности состоит в увеличении объема выборки. В таком случае график плотности распределения оценки параметра становится более "узким". При выборе критической области руководствуются правилом Неймана – Пирсона: следует так выбирать критическую область, чтобы вероятность При выборе уровня значимости необходимо учитывать мощность критерия при альтернативной гипотезе. Иногда большая мощность критерия оказывается существеннее малого уровня значимости, и его значение выбирают относительно большим, например 0,2. Такой выбор оправдан, если последствия ошибок второго рода более существенны, чем ошибок первого рода. Например, если отвергнуто правильное решение "продолжить работу пользователей с текущими паролями", то ошибка первого рода приведет к некоторой задержке в нормальном функционировании системы, связанной со сменой паролей. Если же принято решения не менять пароли, несмотря на опасность несанкционированного доступа посторонних лиц к информации, то эта ошибка повлечет более серьезные последствия. В зависимости от сущности проверяемой гипотезы и используемых мер расхождения оценки характеристики от ее теоретического значения применяют различные критерии. Но процедура проверки нулевой гипотезы
1. для выборки по соответствующей формуле вычисляется значение статистики выбранного для проверки гипотезы критерия 2. выбирается уровень значимости 3. определяется критическая область, границы которой зависят от свойств критерия, выбранного уровня значимости, а также вида альтернативной гипотезы (односторонней, двусторонней); 4. принимается решение: если вычисленное значение статистики попадает в критическую область, нулевая гипотеза отклоняется, и принимается альтернативная. Если нет - принимается нулевая гипотеза, после чего по специальным формулам определяется мощность критерия (вероятность того, что решение о принятии нулевой гипотезы не является ошибочным). Формулы и таблицы для вычисления критериев, определения их мощности и критических областей можно найти в учебной и справочной статистической литературе.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 750; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.52.94 (0.012 с.) |
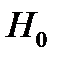 и альтернативную ей
и альтернативную ей  , потом по справочникам или руководствам подобрать подходящий статистический критерий. Затем вычислить значение этого критерия для конкретной анализируемой ситуации, и определить, какой области принадлежит это вычисленное значение критерия. Если вычисленное значение критерия принадлежит критической области, то нулевую гипотезу отвергают, отклоняют. Если вычисленное значение критерия принадлежит области принятия гипотезы, то утверждают, что нет оснований отклонить нулевую гипотезу, фактически, утверждают, что её принимают.
, потом по справочникам или руководствам подобрать подходящий статистический критерий. Затем вычислить значение этого критерия для конкретной анализируемой ситуации, и определить, какой области принадлежит это вычисленное значение критерия. Если вычисленное значение критерия принадлежит критической области, то нулевую гипотезу отвергают, отклоняют. Если вычисленное значение критерия принадлежит области принятия гипотезы, то утверждают, что нет оснований отклонить нулевую гипотезу, фактически, утверждают, что её принимают.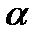 . Как правило, уровень значимости задаётся исследователями. Наиболее часто в социальных и психологических исследованиях используется уровень значимости 0,9, 0,95 или 0,99.
. Как правило, уровень значимости задаётся исследователями. Наиболее часто в социальных и психологических исследованиях используется уровень значимости 0,9, 0,95 или 0,99. . Вероятность несовершения ошибки второго рода равна
. Вероятность несовершения ошибки второго рода равна 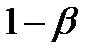 . Эта вероятность называется мощностью статистического критерия. Чем выше вероятность
. Эта вероятность называется мощностью статистического критерия. Чем выше вероятность 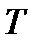 , который используется для принятия решения. Площади под этой кривой – это вероятности соответствующих событий: принятия или отклонения нулевой гипотезы
, который используется для принятия решения. Площади под этой кривой – это вероятности соответствующих событий: принятия или отклонения нулевой гипотезы 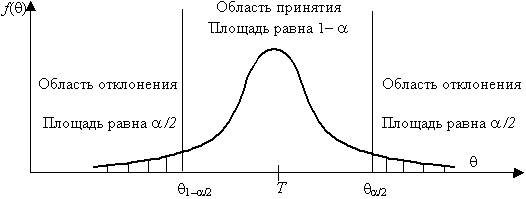
 равно
равно 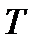 . Если рассматривать гипотезу
. Если рассматривать гипотезу 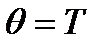 , то при проверке этой гипотезы необходимо оценить, насколько велико должно быть различие между
, то при проверке этой гипотезы необходимо оценить, насколько велико должно быть различие между  и
и 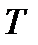 , чтобы эту гипотезу отвергнуть. Ответить на данный вопрос можно в статистическом смысле, рассматривая вероятность достижения некоторой заданной разности между
, чтобы эту гипотезу отвергнуть. Ответить на данный вопрос можно в статистическом смысле, рассматривая вероятность достижения некоторой заданной разности между  и
и  на основе выборочного распределения параметра
на основе выборочного распределения параметра  и
и  , составляет величину
, составляет величину 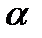 . Эту величину следует выбрать настолько малой, чтобы выход за пределы интервала был маловероятен. Если оценка параметра попала в заданный интервал, то в таком случае нет оснований подвергать сомнению проверяемую гипотезу, следовательно, гипотезу равенства
. Эту величину следует выбрать настолько малой, чтобы выход за пределы интервала был маловероятен. Если оценка параметра попала в заданный интервал, то в таком случае нет оснований подвергать сомнению проверяемую гипотезу, следовательно, гипотезу равенства  , т.е. равна уровню значимости критерия.
, т.е. равна уровню значимости критерия.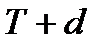 , то согласно гипотезе
, то согласно гипотезе 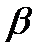 , как видно из Рис. 2.
, как видно из Рис. 2.
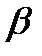 , т.е. снижается мощность критерия. Аналогичные рассуждения можно провести для случая, когда истинное значение параметра равно
, т.е. снижается мощность критерия. Аналогичные рассуждения можно провести для случая, когда истинное значение параметра равно 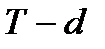 .
. остаётся всегда одинаковой и состоит в следующем:
остаётся всегда одинаковой и состоит в следующем: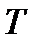 ;
;


