
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическая оценка генеральной дисперсии
По аналогии со статистической оценкой среднего в генеральной совокупности можно предположить, что статистической оценкой генеральной дисперсии будет выборочная дисперсия. Однако такой вывод не будет правильным. Пусть сделана выборка Обозначим Обозначим Докажем, что статистика
По свойствам дисперсии статистика Поэтому, исследуя статистику Поскольку в нашем случае Вычислим теперь математическое ожидание статистики
Действительно, Можно доказать, что статистика В соответствии с этой формулой несмещённой оценкой стандартного квадратичного отклонения генеральной совокупности является величина Реализация несмещённой оценки дисперсии генеральной совокупности может быть выражена формулой: Заметим также, что при больших
|
|||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 685; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.207.183 (0.006 с.) |
 из распределения
из распределения 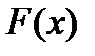 для случайной величины
для случайной величины  . Независимые измерения или наблюдения
. Независимые измерения или наблюдения 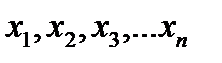 являются реализацией этой выборки.
являются реализацией этой выборки. . Статистика
. Статистика  называется выборочным средним и используется в качестве точечной оценки среднего генеральной совокупности.
называется выборочным средним и используется в качестве точечной оценки среднего генеральной совокупности.  .
. . Статистика
. Статистика  называется выборочной дисперсией, она является также и случайной величиной. Реально для вычислений используется значение этой статистики
называется выборочной дисперсией, она является также и случайной величиной. Реально для вычислений используется значение этой статистики  , которое получается как дисперсия значений реализации этой выборки:
, которое получается как дисперсия значений реализации этой выборки:  .
. . Это представление обосновывается следующими алгебраическими преобразованиями:
. Это представление обосновывается следующими алгебраическими преобразованиями: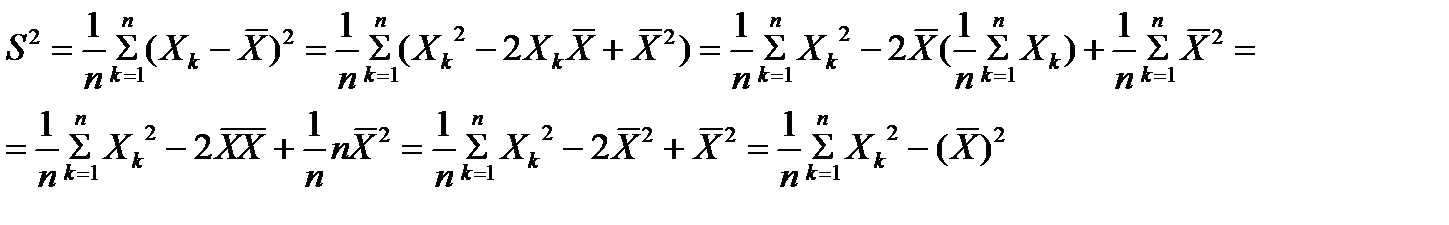
 . Действительно, в этом случае среднее сдвинется на ту же величину:
. Действительно, в этом случае среднее сдвинется на ту же величину:  , все разности случайных величин
, все разности случайных величин  не изменятся:
не изменятся:  . Поскольку не изменятся все такие разности, не изменится и значение статистики
. Поскольку не изменятся все такие разности, не изменится и значение статистики  . Действительно, по определению дисперсии
. Действительно, по определению дисперсии  . Раскроем скобки, пользуясь формулой квадрата разности:
. Раскроем скобки, пользуясь формулой квадрата разности: 
 , получается, что
, получается, что  . С другой стороны, дисперсия каждой случайной величины из выборки равна дисперсии генеральной совокупности:
. С другой стороны, дисперсия каждой случайной величины из выборки равна дисперсии генеральной совокупности:  . Следовательно,
. Следовательно, 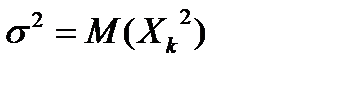 . Кроме того,
. Кроме того, 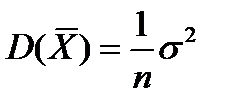 , а в нашем случае нулевых математических ожиданий случайных величин
, а в нашем случае нулевых математических ожиданий случайных величин  . Поэтому дисперсия этой случайной величины равна:
. Поэтому дисперсия этой случайной величины равна:  .
. . Получилось, что статистика
. Получилось, что статистика  является смещенной оценкой дисперсии генеральной совокупности
является смещенной оценкой дисперсии генеральной совокупности 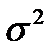 . А несмещённой оценкой дисперсии генеральной совокупности будет статистика
. А несмещённой оценкой дисперсии генеральной совокупности будет статистика 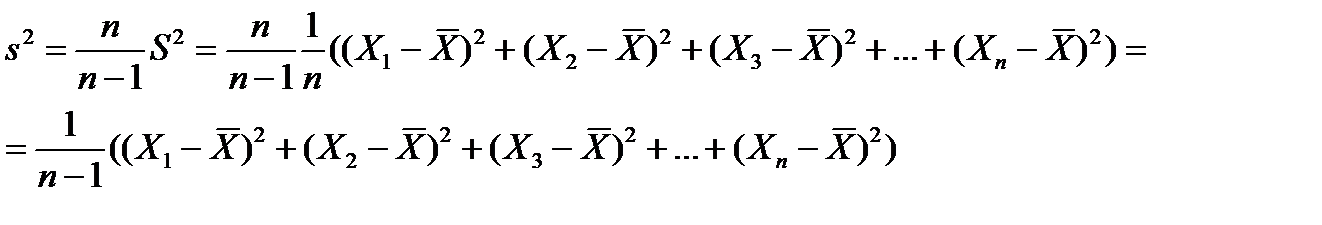
 .
. является не только несмещённой оценкой генеральной дисперсии, но также и состоятельной её оценкой. Но можно также доказать, что эта оценка не является эффективной.
является не только несмещённой оценкой генеральной дисперсии, но также и состоятельной её оценкой. Но можно также доказать, что эта оценка не является эффективной. .
. . Здесь независимые измерения или наблюдения
. Здесь независимые измерения или наблюдения  различие между статистиками
различие между статистиками  будет незначительным. Поэтому при больших
будет незначительным. Поэтому при больших 


