
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функция распределения случайной величины и её свойства
Для анализа случайных величин в теории вероятностей принято использовать её функцию распределения. В отличие от ряда распределения функция распределения может быть определена для случайных величин любых типов. Функцией распределения Можно пояснить, что значение функции распределения Функция распределения случайной величины Функция распределения для любой случайной величины обладает следующими основными свойствами: 1. Функция распределения является неубывающей, т.е. если 2. Функция распределения при стремлении аргумента к 3. Функция распределения является непрерывной слева, т.е. 4. Вероятность того, что случайная величина Первое основное свойство функции распределения можно обосновать так. Если
Второе и третье свойства функции распределения принимаются в этой части курса без доказательства. Отметим только, что оба эти свойства являются следствиями аксиом непрерывности вероятности, которые излагались в первой части курса теории вероятностей и математической статистики. Четвёртое свойство можно обосновать так. Если два числа связаны неравенством Если в последнем равенстве сделать
|
|||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 1108; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.134.78.106 (0.007 с.) |
 случайной величины
случайной величины  называется функция, значениями которой являются вероятности того, что значения случайной величины
называется функция, значениями которой являются вероятности того, что значения случайной величины  будут строго меньше аргумента функции распределения
будут строго меньше аргумента функции распределения  . Следовательно, функция распределения случайной величины
. Следовательно, функция распределения случайной величины  и значения функции распределения задаются так:
и значения функции распределения задаются так:  .
. – это вероятность того, что случайная величина
– это вероятность того, что случайная величина  . Для всех остальных значений своего аргумента
. Для всех остальных значений своего аргумента  .
. , то
, то  .
. стремится к 0, а при стремлении к
стремится к 0, а при стремлении к  стремится к 1. Иначе говоря,
стремится к 1. Иначе говоря,  , а
, а  .
. .
. , в который левый конец
, в который левый конец  включён, а правый конец
включён, а правый конец  - нет, равна разности значений функции распределения этой случайной величины в концах этого полуинтервала:
- нет, равна разности значений функции распределения этой случайной величины в концах этого полуинтервала:  .
. является подмножеством
является подмножеством  . Следовательно, случайное событие
. Следовательно, случайное событие  является подмножеством случайного события
является подмножеством случайного события  . И тогда по определению функции распределения получаем, что
. И тогда по определению функции распределения получаем, что  , то объединение множеств
, то объединение множеств  и
и  даст множество
даст множество  , т.е.
, т.е.  . Равны и вероятности этих множеств, как случайных событий:
. Равны и вероятности этих множеств, как случайных событий: 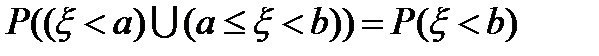 . При этом множества
. При этом множества  не пересекаются, а потому являются несовместными случайными событиями. Для таких случайных событий вероятность их объединения равна сумме их вероятностей:
не пересекаются, а потому являются несовместными случайными событиями. Для таких случайных событий вероятность их объединения равна сумме их вероятностей: 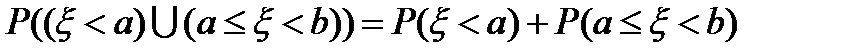 . Следовательно,
. Следовательно, 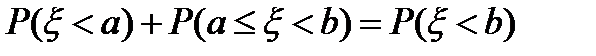 или
или  . И тогда по определению того, как вычисляются значения функции распределения, вероятности в правой части этого равенства можно заменить значениями функции распределения от соответствующих значений аргументов:
. И тогда по определению того, как вычисляются значения функции распределения, вероятности в правой части этого равенства можно заменить значениями функции распределения от соответствующих значений аргументов:  .
. переменной и устремить к
переменной и устремить к  справа, то получится, что в пределе полуинтервал превратится в точку
справа, то получится, что в пределе полуинтервал превратится в точку  , а само равенство превратится в
, а само равенство превратится в 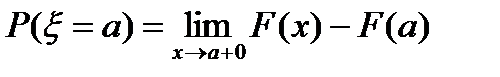 . Выражение в правой части этого равенства называется скачком функции
. Выражение в правой части этого равенства называется скачком функции 


