
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Другие характеристики центральных тенденций и изменчивости распределений случайных величин
Числовые характеристики случайных величин можно условно разделить на основные и вспомогательные. К основным характеристикам относятся характеристики положения случайной величины и характеристики рассеяния. Характеристики положения указывают некоторую точку на числовой оси, вокруг которой группируются возможные значения случайной величины. К ним относятся математическое ожидание, мода и медиана случайной величины. Характеристики рассеяния являются некоторой мерой разброса возможных значений случайной величины около своего центра рассеяния, например, математического ожидания. Характеристиками рассеяния являются дисперсия и стандартное отклонение случайной величины, которая полностью определяется дисперсией, но может быть удобна в практическом применении. Дополнительные числовые характеристики случайных величин применяются для дальнейшего уточнения их свойств. К таким характеристикам, прежде всего, относятся асимметрия (или скошенность) и эксцесс (или островершинность) закона распределения случайной величины. К дополнительным характеристикам относится и коэффициент вариации случайной величины, который характеризует относительный разброс возможных значений случайной величины. Математическое ожидание и дисперсия случайной величины вместе со стандартным отклонением были описаны выше. Опишем теперь другие числовые характеристики случайных величин. Мода Модой непрерывной случайной величины X называется такое значение x, при котором плотность распределения вероятностей случайной величины p(x) принимает максимальное значение. Модой для дискретной случайной величины является её наивероятнейшее значение, на практике – наиболее частое значение. Мода обозначается через Mo. Таким образом, мода – это наиболее часто встречающееся значение в наборе данных. В случае, если данные сгруппированы и построено распределение частот, модой является значение в данных, имеющее наибольшую частоту. Моду можно использовать для измерения центральной тенденции распределения, как дискретных, так и непрерывных случайных величин. Но необходимо учитывать и ограничения в применении моды для такого использования: мода показывает только расположение наиболее частого значения в данных, но не позволяет учесть другие важные особенности распределения, например, число наблюдений выше или ниже моды, расстояния между модами, если их в распределении несколько, и т.п.
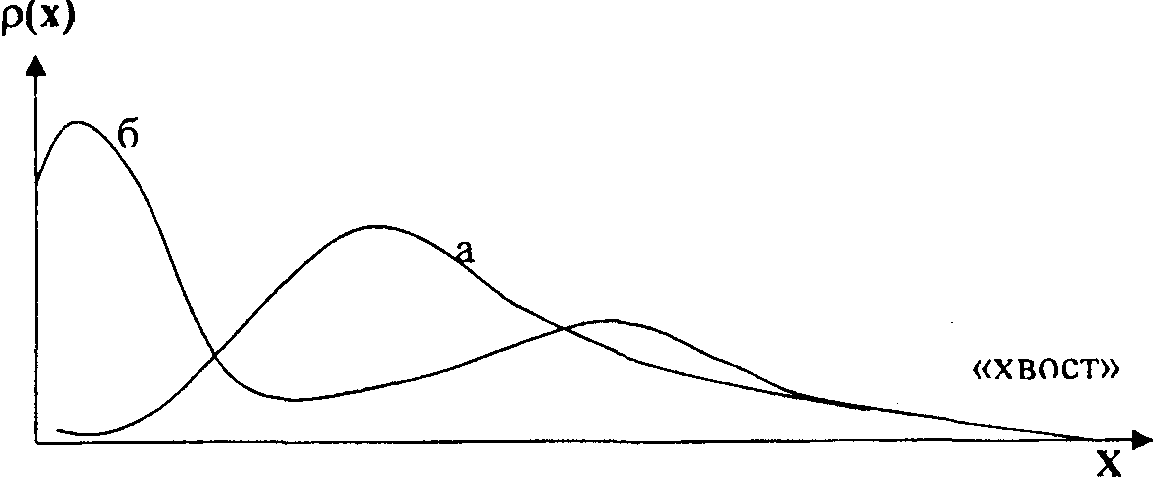
Для нахождения моды непрерывной случайной величины нужно исследовать плотность распределения вероятностей на максимум. Для этого нужно найти стационарные точки, как корни уравнения p′(x) = 0, затем применить к найденным точкам один из достаточных признаков максимума. Если максимумов вообще нет, то говорят, что моды не существует. Если максимум один, то закон распределения называют одномодальным, если максимумов несколько, то – многомодальным. На рисунке ниже представлены одномодальное распределение (а) и бимодальное или двухмодальное распределение (б).
Рисунок. Одномодальное распределение (а) и бимодальное распределение (б)
Таким образом, получается, что мода – это локальная, а не глобальная характеристика непрерывного случайного распределения. Ведь для глобальной характеристики всегда получалась бы одна единственная мода – значение с максимальной частотой. Но и в теории и в практике понимание моды как локальной характеристики непрерывного случайного распределения стало уже общепринятым. Необходимо отметить, что бывают и распределения, имеющие три и более мод, но при большом числе мод описание распределения в терминах наиболее частых значений уже, как правило, теряет смысл. Для определения моды дискретной случайной величины необходимо построить её ряд распределения, а в нём выбрать значение, для которого абсолютная или относительная частота будет максимальной. Пример. Пусть распределение проданной в магазине женской обуви по размерам характеризуется следующим образом:
В этом ряду распределения модой является 37 размер, потому что с этим размером было продано больше всего обуви – 108 пар. Следовательно, в этом примере Мо=37. Но бывает, что данные заданы интервалами значений частот, а не конкретными их значениями для каждого отдельного данного. Для интервальных данных определение моды несколько сложнее, и её невозможно определить точно. Общепринятой является такая процедура определения моды в этих случаях. Сначала нужно найти интервал значений данных, для которого суммарная частота является наибольшей. Этот интервал можно назвать модальным интервалом, т.е. интервалом, частота которого максимальна относительно других интервалов.
В самом простом варианте для интервальных данных модой считается середина этого модального интервала. Для большей обоснованности определения моды для интервальных данных делается некоторое общепринятое допущение о том, что интервалы выше и ниже модального в зависимости от своей частоты имеют разные веса и влияют на положение моды, как бы перетягивают моду в свою сторону. Если частота интервала следующего за модальным больше, чем частота интервала перед модальным, то мода будет правее середины модального интервала и наоборот. Общепринятой формулой расчёта моды с учётом весов интервалов, прилегающих к модальному, является такая:
где В электронных таблицах, например, в Microsoft Excel, почти всегда есть встроенные функции для вычисления моды. В русскоязычной версии Microsoft Excel такая функция так и называется =МОДА(), она вычисляет моду для массива или одного интервала значений. Но эта функция не подходит для вычисления моды для интервальных данных, с несколькими интервалами значений. Пример. Пусть распределение сотрудников по стажу их работы характеризуется следующими данными.
В самом простом варианте медианным стажем работы сотрудников можно считать 7 лет, потому что медианным является интервал данных от 6 до 8 лет стажа, а среднее арифметическое концов этого интервала даёт его середину, т.е. Мо=(6+8)/2=7. С учётом ближайших к модальному интервалов моду нужно вычислять по более сложной формуле: Для вычисления моды непрерывной случайной величины необходимо находить экстремумы её плотности распределения. Пример. Найти моду следующей непрерывной случайной величины, заданной своей плотностью:
Сначала найдём производную от плотности:
Медиана Медианой случайной величины X называется такое её значение Me, которое разбивает всю область возможных значений случайной величины на две равновероятные части, т.е. для этого значения должно быть:
Из определения следует, что медиана, как и мода, точно может быть определена для непрерывных случайных величин, а для дискретных – не всегда. По определению, медиана находится как решение уравнения F(x) = 0,5, где F(x) – это функция распределения случайной величины, потому что по определению
Рисунок. Медиана – это аргумент функции распределения, который даёт её значение 0,5. В некоторых задачах для дискретных случайных величин за медиану принимается некоторое значение x, достаточно близкое к решению указанного уравнения. В случае симметричных распределений медиана совпадает с математическим ожиданием случайной величины. Если, к тому же, распределение является одномодальным, то совпадают все три характеристики – математическое ожидание, мода и медиана. В электронных таблицах, например, в Microsoft Excel, почти всегда есть встроенные функции для вычисления медианы. В русскоязычной версии Microsoft Excel такая функция так и называется =МЕДИАНА(), она вычисляет медиану, как для предварительно упорядоченных, так и для неупорядоченных массивов значений. Пример. Проводилось тестирование 11 человек на уровень интеллекта по тесту IQ. Результаты приведены в следующей таблице:
Необходимо определить моду и медиану для этого распределения значений. Модой является наиболее часто встречающееся значение. Поэтому необходимо просто подсчитать, сколько раз в этом ряду распределения встречается каждое значение:
Чаще всего (5 раз) встречается значение IQ=110, это и есть мода данного распределения. В этой же таблице значения случайной величины упорядочены слева направо по возрастанию значений. Такое упорядочение позволяет определить значение случайной величины, левее которой и правее которой будет одинаковое число значений, в нашем случае – по 2. Таким срединным значением будет IQ=100, это и есть медиана данного распределения. Но так можно определить медиану только для распределения с нечётным числом различных значений. Если число таких значений будет чётным, нужно брать среднее арифметическое из двух значений, которые находятся в середине упорядоченного ряда значений случайной величины. Пример. Снова проводилось тестирование 11 человек на уровень интеллекта по тесту IQ. Результаты приведены в следующей таблице (только у 11 испытуемого теперь IQ=115):
Необходимо определить моду и медиану для этого распределения значений. Модой является наиболее часто встречающееся значение. Поэтому необходимо просто подсчитать, сколько раз в этом ряду распределения встречается каждое значение:
Чаще всего (теперь 4 раза) снова встречается значение IQ=110, это и есть мода данного распределения. В этой же таблице значения случайной величины упорядочены слева направо по возрастанию значений. Такое упорядочение позволяет определить значение случайной величины, левее которой и правее которой будет одинаковое число значений. Но теперь это получилось не одно значение, а два, т.е. 100 и 110, левее и правее которых в нашем случае – по 2 значения. Тогда срединным значением в распределении будет Квантили Кроме моды и медианы ряды распределений могут характеризоваться квантилями, понятие которых является обобщением понятия медианы. Квантили предназначены для более глубокого изучения структуры ряда распределения, потому что квантиль – это значение признака, занимающее определенное место в упорядоченной по данному признаку совокупности данных. Более точно: «квантиль порядка p», который обозначается
Медиана является частным случаем квантиля, потому что Как правило, для характеристики распределений случайных величин, за исключением случая медианы, выбирают не один, а серию квантилей, расположенных на числовой оси на одинаковых расстояниях друг от друга. Наиболее употребительны для этих целей квартили, которые делят распределение на 4 части, децили, которые делят распределение на 10 частей, а также перцентили, которые делят распределение на 100 частей. Для квартилей часто используют такие обозначения: Для расчета квартилей в версиях Microsoft Excel до 2007 г. использовалась функция =КВАРТИЛЬ(массив;часть). Начиная с версии Microsoft Excel 2010, применяются две функции: =КВАРТИЛЬ.ВКЛ(массив;часть) и =КВАРТИЛЬ.ИСКЛ(массив;часть), дающие несколько различающиеся значения. При этом функция =КВАРТИЛЬ, использовавшаяся ранее соответствует, современной функции =КВАРТИЛЬ.ВКЛ. Для расчета квартилей в Microsoft Excel с помощью вышеприведенных формул массив данных можно не упорядочивать. В анализе статистических данных нередко используется так называемый квартильный размах Децили – это значения признака, которые ранжированный ряд распределения делят на 10 равных частей. Расчеты ведутся аналогично расчетам квартилей: В некоторых случаях вместо децилей используют процентили. Перцентили – это значения признака, делящие ранжированный ряд распределения на 100 равных частей. Все вычисления аналогичны вычислениям децилей и квартилей: Нужно ли использовать квантили и какие именно, определяется, как правило, спецификой задачи анализа данных и опытом исследователя.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 1315; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.143.31 (0.023 с.) |
 ,
, - это мода,
- это мода, 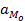 - значение начала модального интервала (его левая граница),
- значение начала модального интервала (его левая граница),  - ширина модального интервала (от левой до правой границы),
- ширина модального интервала (от левой до правой границы),  - частота модального интервала,
- частота модального интервала,  - частота интервала непосредственно предшествующего модальному, а
- частота интервала непосредственно предшествующего модальному, а  - частота интервала непосредственно следующего за модальным. Следовательно, в этой формуле мода интервального ряда представляет собой сумму значения начального уровня модального интервала и ширины отрезка, который определяется соотношением частоты ближайших к модальному интервалов.
- частота интервала непосредственно следующего за модальным. Следовательно, в этой формуле мода интервального ряда представляет собой сумму значения начального уровня модального интервала и ширины отрезка, который определяется соотношением частоты ближайших к модальному интервалов.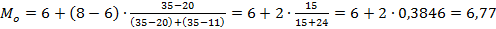 . Это, безусловно, приближённое значение моды, но в данном случае точно её значение определить невозможно. И на практике считается, что этот второй вариант определения моды для интервального ряда распределения точнее даёт её значение, чем для простого варианта с серединой интервала.
. Это, безусловно, приближённое значение моды, но в данном случае точно её значение определить невозможно. И на практике считается, что этот второй вариант определения моды для интервального ряда распределения точнее даёт её значение, чем для простого варианта с серединой интервала.
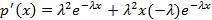 =
=  . Теперь решим уравнение
. Теперь решим уравнение 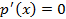 . Приравняем к нулю результат вычисления этой производной:
. Приравняем к нулю результат вычисления этой производной:  . В левой части два сомножителя больше нуля:
. В левой части два сомножителя больше нуля:  по условию задачи, а
по условию задачи, а  , потому что значения показательной функции всегда больше нуля. Получается, что нулю может равняться только последний, третий сомножитель:
, потому что значения показательной функции всегда больше нуля. Получается, что нулю может равняться только последний, третий сомножитель:  . Решая это линейное уравнение, получаем:
. Решая это линейное уравнение, получаем: 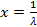 . В этой точке плотность вероятности будет иметь максимум, потому что величина
. В этой точке плотность вероятности будет иметь максимум, потому что величина  при
при  , т.е. левее
, т.е. левее  величина
величина  ,, т.е. правее
,, т.е. правее 
 . Очевидно, что для дискретных величин это уравнение не всегда имеет решение, может иметь даже бесконечное множество решений в силу ступенчатого характера функции распределения вероятностей. Графическое решение этого уравнения показано на следующем рисунке.
. Очевидно, что для дискретных величин это уравнение не всегда имеет решение, может иметь даже бесконечное множество решений в силу ступенчатого характера функции распределения вероятностей. Графическое решение этого уравнения показано на следующем рисунке.
 , это и есть медиана данного распределения. Хотя такого значения IQ=105 в данном ряду распределения нет.
, это и есть медиана данного распределения. Хотя такого значения IQ=105 в данном ряду распределения нет. , и для которого 0<p<1, потому что p – это вероятность, – это значение случайной величины, для которого функция распределения принимает значение p или имеет место «скачок» со значения меньше p до значения больше p. Иначе говоря, «квантиль порядка p» - это такое значение аргумента функции распределения случайной величины, что
, и для которого 0<p<1, потому что p – это вероятность, – это значение случайной величины, для которого функция распределения принимает значение p или имеет место «скачок» со значения меньше p до значения больше p. Иначе говоря, «квантиль порядка p» - это такое значение аргумента функции распределения случайной величины, что  . Поскольку по определению функции распределения
. Поскольку по определению функции распределения  , можно говорить, что
, можно говорить, что  , для которого вероятность
, для которого вероятность  . Для непрерывных функций распределения, как правило, существует единственная квантиль
. Для непрерывных функций распределения, как правило, существует единственная квантиль  , ведь оба эти значения определяют середину распределения:
, ведь оба эти значения определяют середину распределения:  и
и  дл квантиля
дл квантиля  .
. ,
,  ,
, 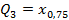 ,
,  Квартиль
Квартиль  используется крайне редко, потому что он просто характеризует всё распределение. А 1-й квартиль – это значение, ниже которого находится 25% совокупности. 2-й квартиль делит совокупность данным пополам (это совпадает с медианой), а 3-й квартиль отделяет 25% наибольших значений.
используется крайне редко, потому что он просто характеризует всё распределение. А 1-й квартиль – это значение, ниже которого находится 25% совокупности. 2-й квартиль делит совокупность данным пополам (это совпадает с медианой), а 3-й квартиль отделяет 25% наибольших значений. – это разница между 3-м и 1-м квартилями, т.е.
– это разница между 3-м и 1-м квартилями, т.е.  . Эта величина позволяет оценить разброс 50% элементов в распределении случайной величины и не учитывать влияние экстремальных элементов. У квартильного размаха
. Эта величина позволяет оценить разброс 50% элементов в распределении случайной величины и не учитывать влияние экстремальных элементов. У квартильного размаха  , что означает выполнение соотношения
, что означает выполнение соотношения  . При этом децили не совпадают с квартилями, кроме второго или медианы, когда это совпадение есть:
. При этом децили не совпадают с квартилями, кроме второго или медианы, когда это совпадение есть:  . Аналогично квартильному нередко используют децильный размах:
. Аналогично квартильному нередко используют децильный размах:  . Децильный размах в распределении доходов населения показывает, например, долю тех, кто имеет средние доходы – не бедствует, но и не является очень богатым.
. Децильный размах в распределении доходов населения показывает, например, долю тех, кто имеет средние доходы – не бедствует, но и не является очень богатым. . Процентили позволяют вычислять как квартильный размах:
. Процентили позволяют вычислять как квартильный размах: 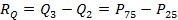 , так и децильный размах:
, так и децильный размах:  .
.


