
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условная вероятность, независимые события и формула умножения вероятностей
Условной вероятностью события A по отношению к событию B называется вероятность события A, вычисленная при условии, что событие B произошло. Обозначается такая условная вероятность как P(A|B), а читается – так: «P от A при условии B». Условная вероятность обладает всеми свойствами безусловной вероятности, потому что тоже является вероятностью. В частности, Вероятность произведения событий выражается через условную вероятность: Докажем формулу умножения вероятностей для классического определения вероятностей. Вероятность произведения событий по классическому определению – это Необходимо помнить, что формула умножения вероятностей может быть доказана и для любых других определений вероятности. Как правило, для этих целей проводят одно доказательство для аксиоматического определения вероятности, т.е. её общего математического определения, из которого следуют доказательства и для всех других определений вероятности, согласованных с этим аксиоматическим. Но такое доказательство сложнее, и по этой причине здесь не приводится.
Если условная вероятность совпадает с безусловной вероятностью, т.е. Если события A и B статистически независимы, то из формулы умножения вероятностей Несовместность событий и их независимость – это разные свойства событий. Например, если несовместные события имеют ненулевые вероятности, то они зависимы. Действительно, если события A и B несовместны, то они не могут осуществиться одновременно, а потому вероятность их произведения равна нулю: Пример. Вероятность выпадения «герба» или «решки» при подбрасывании монеты равняется 1/2. Но вероятность их одновременного выпадения равна нулю, поскольку они несовместны. Значит эти события зависимы, т.е. статистически связаны между собой. Пример. В урне находится 2 белых и 3 чёрных шара. Из урны вынимают подряд два шара и назад в урну они оба раза не возвращаются. Найти вероятность того, что оба вынутых шара окажутся белыми. Благоприятным событием A в этом примере является появление двух белых шаров из урны. Это событие является произведением двух событий: A1 – первый вынутый шар белый и A2 – второй вынутый шар белый. Тогда можно вычислить вероятность благоприятного события:
Вероятность похожего события B будет иной, если при такой же выемке шаров их потом снова возвращают в урну, просто фиксируя, какого цвета был вынутый шар. Если событие B в этой новой ситуации будет тоже состоять в том, что будут вынуты два белых шара, то выемка каждого из них будет осуществляться независимо от другого. Тогда снова событие B является произведением двух событий: A1 – первый вынутый шар белый и A2 – второй вынутый шар белый. Но теперь события A1 и A2 являются независимыми друг от друга. Поэтому Пример. Два стрелка одновременно, независимо друг от друга стреляют по мишени. Вероятность попадания в мишень для первого стрелка равна 0,6, а для второго – 0,8. Какова вероятность того, что в мишени окажется две пробоины? Пусть событие A – попадание в мишень первым стрелком, событие B – попадание в мишень вторым стрелком, событие C – в мишени оказалось две пробоины, т.е. оба стрелка попали в мишень. Тогда C = AB, причём события A и B являются независимыми по условию задачи. Следовательно, вероятность
|
||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 1450; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.127.141 (0.006 с.) |
 . Отметим также, что если B ⊂ A, то P(A|B) = 1, потому что при осуществлении B как части множества A событие A обязательно осуществляется через элементарные события, входящие в B. Кроме того, если
. Отметим также, что если B ⊂ A, то P(A|B) = 1, потому что при осуществлении B как части множества A событие A обязательно осуществляется через элементарные события, входящие в B. Кроме того, если 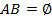 , то P(A|B) = 0, потому что при осуществлении события B событие A никак не может осуществиться, ведь у A и B нет никаких общих элементарных событий.
, то P(A|B) = 0, потому что при осуществлении события B событие A никак не может осуществиться, ведь у A и B нет никаких общих элементарных событий. . Поскольку значение вероятности не изменится при смене порядка написания произведения событий AB=BA, то получается, что
. Поскольку значение вероятности не изменится при смене порядка написания произведения событий AB=BA, то получается, что  . Эта формула называется формулой умножения вероятностей. Из неё можно получить формулу для вычисления условной вероятности:
. Эта формула называется формулой умножения вероятностей. Из неё можно получить формулу для вычисления условной вероятности:  . И аналогично из первого варианта этой формулы умножения вероятностей получается, что
. И аналогично из первого варианта этой формулы умножения вероятностей получается, что  .
. , где N – это общее число возможных исходов опыта, а NAB – число благоприятных таких исходов. Условную вероятность можно представить так:
, где N – это общее число возможных исходов опыта, а NAB – число благоприятных таких исходов. Условную вероятность можно представить так:  , потому что это вероятность при условии, что событие B произошло, т.е. при общем числе исходов NB. А благоприятных исходов здесь будет NAB, потому что произошло и событие A, и событие B. Ведь событие A осуществилось при условии осуществления и события B. Преобразуем формулу, разделив и числитель и знаменатель дроби на одно и то же число NB, не равное нулю, что не изменит значения этой дроби:
, потому что это вероятность при условии, что событие B произошло, т.е. при общем числе исходов NB. А благоприятных исходов здесь будет NAB, потому что произошло и событие A, и событие B. Ведь событие A осуществилось при условии осуществления и события B. Преобразуем формулу, разделив и числитель и знаменатель дроби на одно и то же число NB, не равное нулю, что не изменит значения этой дроби:  . В этой формуле первая дробь – это условная вероятность
. В этой формуле первая дробь – это условная вероятность  . В результате получаем:
. В результате получаем:  , т.е. один из вариантов формулы умножения вероятностей.
, т.е. один из вариантов формулы умножения вероятностей. , то события A и B называются статистически независимыми событиями. Это значит, что вероятность осуществления события A не зависит от того, произошло или нет событие B. В противном случае, когда
, то события A и B называются статистически независимыми событиями. Это значит, что вероятность осуществления события A не зависит от того, произошло или нет событие B. В противном случае, когда  , события A и B называются статистически завиcимыми событиями. Можно доказать, что статистическая зависимость или независимость является взаимной, т.е. если
, события A и B называются статистически завиcимыми событиями. Можно доказать, что статистическая зависимость или независимость является взаимной, т.е. если  . Действительно,
. Действительно,  . Если эти вероятности равны
. Если эти вероятности равны  получается
получается  . Разделив обе части этого равенства на N, а потом на NA, получаем:
. Разделив обе части этого равенства на N, а потом на NA, получаем:  , т.е. что
, т.е. что  , потому что для независимых событий
, потому что для независимых событий  . И, если бы события A и B были независимы, то была бы верна формула:
. И, если бы события A и B были независимы, то была бы верна формула:  и
и 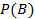 их произведение не может быть равно нулю. Следовательно, события A и B в таких условиях должны быть зависимы.
их произведение не может быть равно нулю. Следовательно, события A и B в таких условиях должны быть зависимы. . Вычислим вероятности, составляющие сомножители этого произведения. Для события A1 благоприятных исходов 2 (можно вынуть первый или второй белый шар), а всего исходов – 5 (потому что столько всего шаров в урне). Поэтому
. Вычислим вероятности, составляющие сомножители этого произведения. Для события A1 благоприятных исходов 2 (можно вынуть первый или второй белый шар), а всего исходов – 5 (потому что столько всего шаров в урне). Поэтому  . При вычислении второй, уже условной вероятности, необходимо учесть, что один белых шар уже вынут из урны, поэтому благоприятных событий будет 1 (в урне остался один белый шар). А всего событий при второй выемке шара будет 4, потому что столько шаров после выемки первого шара в этой урне осталось. Поэтому
. При вычислении второй, уже условной вероятности, необходимо учесть, что один белых шар уже вынут из урны, поэтому благоприятных событий будет 1 (в урне остался один белый шар). А всего событий при второй выемке шара будет 4, потому что столько шаров после выемки первого шара в этой урне осталось. Поэтому  . Тогда по формуле произведения вероятностей получаем:
. Тогда по формуле произведения вероятностей получаем:  .
. . И теперь вероятности обоих событий A1 и A2 будут одинаковыми и равными
. И теперь вероятности обоих событий A1 и A2 будут одинаковыми и равными  , потому что благоприятных событий будет 2 (два шара в урне), а всего возможных событий 5 (всего шаров в урне). И тогда вероятность
, потому что благоприятных событий будет 2 (два шара в урне), а всего возможных событий 5 (всего шаров в урне). И тогда вероятность  . Эта вероятность получилась несколько больше первой.
. Эта вероятность получилась несколько больше первой. .
.


