
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Стохастичность и вероятностьСтр 1 из 46Следующая ⇒
Стохастичность и вероятность Роль математики в развитии понятия о вероятности Математика стала первооткрывателем идей, развитие которых вело к коренной перестройке мировоззренческих представлений и стиля мышления о вероятности и случайности. Теория вероятностей начала формироваться как наука с середины 17 века, когда Б. Паскаль, П. Ферма и Х. Гюйгенс проанализировали ряд задач, возникших на базе азартных игр. Применение вероятностных идей к исследованию физических, биологических и социальных явлений сформировало в середине 19 века у ученых убеждение в почти универсальной применимости вероятностных идей. Сегодня трудно найти сколько-нибудь значительную область научного знания, где бы ни использовались вероятностно-статистические методы. Вероятностные представления, по признанию ученых, обладают большой эвристической ценностью, и эта ценность постоянно возрастает в процессе расширения человеческих знаний. Предмет теории вероятностей Многие явления в окружающем нас мире носят случайный характер, т.е. если явление наблюдать один раз, то нельзя точно предсказать, как оно будет протекать. Но если это явление наблюдать многократно при неизменных условиях, то оказывается, что протекание этого явления можно описать с помощью чисел, т.е. количественно. Примеры: 1. если бросать монету один раз, то нельзя предсказать, что выпадет герб или цифра; 2. посеянное зерно может дать всход, а может и не взойти. Если это наблюдение проводить много раз, то можно заметить закономерность: 1. при подбрасывании монеты отношение числа выпадений герба (цифры) к общему числу подбрасываний очень мало отличается от ½, чем больше наблюдений тем ближе к ½; 2. при посеве зерен отношение числа зерен, давших всходы, к общему числу посеянных зерен мало, чем отличается от некоторого постоянного числа, с возрастанием общего числа зерен. О результатах подобных наблюдений говорят, что они обладают свойством статистической устойчивости. Теория вероятностей дает математические модели для описания случайных явлений, которые могут быть воспроизведены при неизменных условиях сколько угодно много раз и обладающих свойством статистической устойчивости. Приступая к построению математической модели, учитывают главные наиболее существенные особенности изучаемого явления или процесса и отбрасывают те, которые на данном уровне исследований считаются второстепенными.
Так при подбрасывании монеты предполагаются только два возможных исхода – выпадение герба или цифры, возможность падения монеты на ребро или возможность ее исчезновения в результате испытания не учитываются. При высеве семян допущения состоят в том, что семена абсолютно одинакового качества, высаживаются в одинаковых условиях. Различие в качестве, условия высева и произрастания не учитываются, т.е. считаются несущественными. В действительности и качество семян, и условия их посева и произрастания одинаковыми не бывают. При такой постановке задачи выводы, полученные в результате изучения моделей, будут отражать особенности явления лишь в главном, а при решении прикладных задач ответ на поставленный вопрос будет приближенным. Теория вероятностей – это математическая наука о количественных закономерностях моделей случайных явлений независимо от их конкретной природы. Теория вероятностей широко используется в теоретических и прикладных науках: физике, геодезии, теории автоматического управления и т.д. В частности, она служит теоретической базой математической и прикладной статистики, на основе которых осуществляется планирование и организация производства. Определения понятия вероятности Значения вероятности как меры случайности во многом определяются характеристиками тех моделей случайных событий и явлений, которые используются как наиболее адекватные в тех или иных ситуациях. Фактически, различные определения понятия вероятности, изложенные ниже, показывают основные типы таких моделей и, соответственно, как в этих моделях получаются числовые значения вероятностей. Случайные события Математическая теория вероятностей даёт модель реальности, которая может быть более или менее адекватна этой реальности. Адекватная модель всегда включает самые существенные для анализа ситуации объекты и связи между ними. Опишем модель случайного события, которая используется в современной теории вероятностей.
Опыт – это действие, которое при неоднократном повторении может давать различные результаты. Событие – это любое последствие осуществления опыта, любой факт или явление, которое произошло в результате осуществления опыта. Событие называется случайным, если в результате опыта оно может произойти, а может и не произойти. Примеры опытов и случайных событий. 1. Опытом можно считать стрельбу по цели. Событиями можно считать попадание или непопадание в мишень (это разные события). 2. Опытом можно считать подбрасывание монетки. Одно событие тогда – это выпадение орла, другое событие – выпадение решки. Событие называется достоверным, если в результате опыта оно обязательно происходит. Событие называется невозможным, если оно ни при каких условиях не может произойти в результате опыта. Например, достоверным является событие выпадения орла или решки при подбрасывании монетки (какая-то сторона монетки выпадет всегда, на ребро она не встанет, как мы считаем). Два события A и B считаются несовместными, если в результате опыта одновременно они осуществиться не могут, будет осуществлено либо A, либо B, но не оба сразу. Группа событий называется несовместной, если никакие два из них не могут осуществиться одновременно в результате опыта. Например, выпадение орла и выпадение решки при подбрасывании монетки – это несовместные события, т.к. может осуществиться только одно из них. Пример группы несовместных событий – выпадение граней игрального кубика: может выпасть от 1 до 6, но только что-то одно. Группа событий называется полной, если в результате опыта хотя бы одно из них обязательно осуществится, т.е. в этой группе событий есть все варианты осуществления такого опыта. Например, полная группа событий – это выпадение граней игрального кубика: может выпасть от 1 до 6, ничего другого выпасть не может. События называются равновозможными в данном опыте, если у них равные возможности осуществиться, т.е. нет каких-то факторов, способствующих осуществлению одних событий и препятствующих осуществлению других. Например, равновозможны выпадения чисел от 1 до 6 при бросании игрального кубика. Если события составляют полную группу равновозможных событий, то каждое такое событие называется исходом опыта. Событие A называется благоприятствующим событию B, если наступление события A влечёт за собой наступление события B. Субъективная вероятность Субъективная вероятность используется в тех случаях, когда трудно или невозможно вычислить вероятность каким-то из описанных выше способов. В таких случаях экспертам предлагают оценить вероятность того или иного события. Их опыт и знания нередко позволяют определять вероятности наступления тех или иных событий, следовательно, прогнозировать их. Субъективной вероятностью называется заключённая от 0 до 1 численная мера уверенности того или иного субъекта, эксперта, специалиста в наступлении рассматриваемого события. На словах нередко субъективная вероятность выражается большей или меньшей уверенностью эксперта, специалиста в том, что событие A произойдёт. Алгебра случайных событий Со случайными событиями можно осуществлять некоторые операции, которые в результатах тоже будут давать случайные события. Множества с наборами операций, результаты которых являются тоже элементами этих множеств, принято в математике называть алгебрами. Если выполнять такие операции на множестве случайных событий, то получается алгебра случайных событий.
Случайные величины Понятие случайной величины Нестрого можно определить случайную величину как величину, которая в результате опыта или эксперимента принимает одно из множества значений, а какое конкретно – заранее неизвестно. Случайные величины обозначают большими латинскими буквами (X, Y, Z1, …), а их возможные значения – соответствующими малыми буквами (x, y, z, …). Событие, состоящее в том, что случайная величина X примет значение x, по традиции, сложившейся в математике, будем отражать записью X = x. С левой стороны этого равенства стоит имя случайной величины, а справа – принимаемое ею значение. Вероятность этого события будем обозначать P{X = x}. Аналогично, P{X < x} – вероятность того, что случайная величина X примет значение, меньшее, чем x. В некоторых случаях в таких записях вероятностей используют круглые скобки, тогда они получают вид: P(X=x) и P(X<x) соответственно. Случайная величина вводится в теории вероятностей для того, чтобы можно было анализировать не только вероятности появления тех или иных результатов опытов или экспериментов, но и значения тех или иных характеристик этих результатов. Например, опыт может состоять в стрельбе из винтовки по мишени, а случайной величиной в таком случае может быть результат стрельбы, т.е. число выбитых стрелком очков. С одним и тем же случайным событием может быть связано несколько случайных величин. Например, с многократным подбрасыванием монеты могут быть связаны такие случайные величины: число выпавших гербов, число выпавших орлов, превышение числа гербов над числом орлов, доля гербов или доля орлов в общем числе результатов опыта и т.п. Следовательно, случайная величина – это числовая характеристика тех или иных свойств случайных событий. В первой части курса теории вероятностей и математической статистики мы изучали только одну характеристику случайных событий – их вероятности. Случайные величины позволяют изучать много других важных для исследователей и аналитиков их характеристик, которые являются числовыми. Для анализа значений случайных величин, поскольку они являются числовыми, во многих случаях можно использовать методы математического анализа и некоторых других разделов математики. Следовательно, введение в теорию вероятностей понятия случайной величины расширяет возможности применения в теории вероятностей методов математики, которые хорошо отработаны в других её разделах.
Более формальное определение случайной величины является таким. В первой части курса вводилось понятие вероятностного пространства. Напомним, что совокупность объектов Случайной величиной на вероятностном пространстве По определению, все элементы Поскольку Типы случайных величин По типам случайные величины принято делить на дискретные, непрерывные и на величины смешанного типа. Случайная величина, определённая на конечном (дискретном) вероятностном пространстве, называется дискретной. Значения такой случайной величины всегда отделены друг от друга на числовой прямой какими-то промежутками без значений функции – случайной величины. Например, такими являются результаты стрельбы по мишени, подбрасываний монеты и т.п. В математике допускается как конечное, так и бесконечное, но счётное (которое можно перенумеровать натуральными числами: 1, 2, 3, и т.д. до бесконечности) множество значений дискретной случайной величины. Случайные величины, значения которых сплошь заполняют какие-то промежутки значений на числовой прямой, называются непрерывными. Все значения непрерывной случайно величины невозможно перенумеровать натуральными числами. Примерами таких случайных величин являются изменения атмосферного давления в зависимости от времени, время ожидания общественного транспорта пассажирами на остановках и т.п. Ниже будет дано уточнение понятия непрерывной случайной величины. Случайная величина смешанного типа кроме непрерывного множества своих возможных значений имеет ещё возможные значения, изолированные от этого множества, не заполняющие никаких промежутков на числовой прямой, которые можно перенумеровать натуральными числами.
Свойства дисперсии Свойства дисперсии одинаковы для всех типов случайных величин, как и для математических ожиданий. 1. 2. 3. 4. 5. 6.
Мода Модой непрерывной случайной величины X называется такое значение x, при котором плотность распределения вероятностей случайной величины p(x) принимает максимальное значение. Модой для дискретной случайной величины является её наивероятнейшее значение, на практике – наиболее частое значение. Мода обозначается через Mo. Таким образом, мода – это наиболее часто встречающееся значение в наборе данных. В случае, если данные сгруппированы и построено распределение частот, модой является значение в данных, имеющее наибольшую частоту. Моду можно использовать для измерения центральной тенденции распределения, как дискретных, так и непрерывных случайных величин. Но необходимо учитывать и ограничения в применении моды для такого использования: мода показывает только расположение наиболее частого значения в данных, но не позволяет учесть другие важные особенности распределения, например, число наблюдений выше или ниже моды, расстояния между модами, если их в распределении несколько, и т.п. Для нахождения моды непрерывной случайной величины нужно исследовать плотность распределения вероятностей на максимум. Для этого нужно найти стационарные точки, как корни уравнения p′(x) = 0, затем применить к найденным точкам один из достаточных признаков максимума. Если максимумов вообще нет, то говорят, что моды не существует. Если максимум один, то закон распределения называют одномодальным, если максимумов несколько, то – многомодальным. На рисунке ниже представлены одномодальное распределение (а) и бимодальное или двухмодальное распределение (б).
Рисунок. Одномодальное распределение (а) и бимодальное распределение (б)
Таким образом, получается, что мода – это локальная, а не глобальная характеристика непрерывного случайного распределения. Ведь для глобальной характеристики всегда получалась бы одна единственная мода – значение с максимальной частотой. Но и в теории и в практике понимание моды как локальной характеристики непрерывного случайного распределения стало уже общепринятым. Необходимо отметить, что бывают и распределения, имеющие три и более мод, но при большом числе мод описание распределения в терминах наиболее частых значений уже, как правило, теряет смысл. Для определения моды дискретной случайной величины необходимо построить её ряд распределения, а в нём выбрать значение, для которого абсолютная или относительная частота будет максимальной. Пример. Пусть распределение проданной в магазине женской обуви по размерам характеризуется следующим образом:
В этом ряду распределения модой является 37 размер, потому что с этим размером было продано больше всего обуви – 108 пар. Следовательно, в этом примере Мо=37. Но бывает, что данные заданы интервалами значений частот, а не конкретными их значениями для каждого отдельного данного. Для интервальных данных определение моды несколько сложнее, и её невозможно определить точно. Общепринятой является такая процедура определения моды в этих случаях. Сначала нужно найти интервал значений данных, для которого суммарная частота является наибольшей. Этот интервал можно назвать модальным интервалом, т.е. интервалом, частота которого максимальна относительно других интервалов. В самом простом варианте для интервальных данных модой считается середина этого модального интервала. Для большей обоснованности определения моды для интервальных данных делается некоторое общепринятое допущение о том, что интервалы выше и ниже модального в зависимости от своей частоты имеют разные веса и влияют на положение моды, как бы перетягивают моду в свою сторону. Если частота интервала следующего за модальным больше, чем частота интервала перед модальным, то мода будет правее середины модального интервала и наоборот. Общепринятой формулой расчёта моды с учётом весов интервалов, прилегающих к модальному, является такая:
где В электронных таблицах, например, в Microsoft Excel, почти всегда есть встроенные функции для вычисления моды. В русскоязычной версии Microsoft Excel такая функция так и называется =МОДА(), она вычисляет моду для массива или одного интервала значений. Но эта функция не подходит для вычисления моды для интервальных данных, с несколькими интервалами значений. Пример. Пусть распределение сотрудников по стажу их работы характеризуется следующими данными.
В самом простом варианте медианным стажем работы сотрудников можно считать 7 лет, потому что медианным является интервал данных от 6 до 8 лет стажа, а среднее арифметическое концов этого интервала даёт его середину, т.е. Мо=(6+8)/2=7. С учётом ближайших к модальному интервалов моду нужно вычислять по более сложной формуле: Для вычисления моды непрерывной случайной величины необходимо находить экстремумы её плотности распределения. Пример. Найти моду следующей непрерывной случайной величины, заданной своей плотностью:
Сначала найдём производную от плотности: Медиана Медианой случайной величины X называется такое её значение Me, которое разбивает всю область возможных значений случайной величины на две равновероятные части, т.е. для этого значения должно быть:
Из определения следует, что медиана, как и мода, точно может быть определена для непрерывных случайных величин, а для дискретных – не всегда. По определению, медиана находится как решение уравнения F(x) = 0,5, где F(x) – это функция распределения случайной величины, потому что по определению
Рисунок. Медиана – это аргумент функции распределения, который даёт её значение 0,5. В некоторых задачах для дискретных случайных величин за медиану принимается некоторое значение x, достаточно близкое к решению указанного уравнения. В случае симметричных распределений медиана совпадает с математическим ожиданием случайной величины. Если, к тому же, распределение является одномодальным, то совпадают все три характеристики – математическое ожидание, мода и медиана. В электронных таблицах, например, в Microsoft Excel, почти всегда есть встроенные функции для вычисления медианы. В русскоязычной версии Microsoft Excel такая функция так и называется =МЕДИАНА(), она вычисляет медиану, как для предварительно упорядоченных, так и для неупорядоченных массивов значений. Пример. Проводилось тестирование 11 человек на уровень интеллекта по тесту IQ. Результаты приведены в следующей таблице:
Необходимо определить моду и медиану для этого распределения значений. Модой является наиболее часто встречающееся значение. Поэтому необходимо просто подсчитать, сколько раз в этом ряду распределения встречается каждое значение:
Чаще всего (5 раз) встречается значение IQ=110, это и есть мода данного распределения. В этой же таблице значения случайной величины упорядочены слева направо по возрастанию значений. Такое упорядочение позволяет определить значение случайной величины, левее которой и правее которой будет одинаковое число значений, в нашем случае – по 2. Таким срединным значением будет IQ=100, это и есть медиана данного распределения. Но так можно определить медиану только для распределения с нечётным числом различных значений. Если число таких значений будет чётным, нужно брать среднее арифметическое из двух значений, которые находятся в середине упорядоченного ряда значений случайной величины. Пример. Снова проводилось тестирование 11 человек на уровень интеллекта по тесту IQ. Результаты приведены в следующей таблице (только у 11 испытуемого теперь IQ=115):
Необходимо определить моду и медиану для этого распределения значений. Модой является наиболее часто встречающееся значение. Поэтому необходимо просто подсчитать, сколько раз в этом ряду распределения встречается каждое значение:
Чаще всего (теперь 4 раза) снова встречается значение IQ=110, это и есть мода данного распределения. В этой же таблице значения случайной величины упорядочены слева направо по возрастанию значений. Такое упорядочение позволяет определить значение случайной величины, левее которой и правее которой будет одинаковое число значений. Но теперь это получилось не одно значение, а два, т.е. 100 и 110, левее и правее которых в нашем случае – по 2 значения. Тогда срединным значением в распределении будет Квантили Кроме моды и медианы ряды распределений могут характеризоваться квантилями, понятие которых является обобщением понятия медианы. Квантили предназначены для более глубокого изучения структуры ряда распределения, потому что квантиль – это значение признака, занимающее определенное место в упорядоченной по данному признаку совокупности данных. Более точно: «квантиль порядка p», который обозначается Медиана является частным случаем квантиля, потому что Как правило, для характеристики распределений случайных величин, за исключением случая медианы, выбирают не один, а серию квантилей, расположенных на числовой оси на одинаковых расстояниях друг от друга. Наиболее употребительны для этих целей квартили, которые делят распределение на 4 части, децили, которые делят распределение на 10 частей, а также перцентили, которые делят распределение на 100 частей. Для квартилей часто используют такие обозначения: Для расчета квартилей в версиях Microsoft Excel до 2007 г. использовалась функция =КВАРТИЛЬ(массив;часть). Начиная с версии Microsoft Excel 2010, применяются две функции: =КВАРТИЛЬ.ВКЛ(массив;часть) и =КВАРТИЛЬ.ИСКЛ(массив;часть), дающие несколько различающиеся значения. При этом функция =КВАРТИЛЬ, использовавшаяся ранее соответствует, современной функции =КВАРТИЛЬ.ВКЛ. Для расчета квартилей в Microsoft Excel с помощью вышеприведенных формул массив данных можно не упорядочивать. В анализе статистических данных нередко используется так называемый квартильный размах Децили – это значения признака, которые ранжированный ряд распределения делят на 10 равных частей. Расчеты ведутся аналогично расчетам квартилей: В некоторых случаях вместо децилей используют процентили. Перцентили – это значения признака, делящие ранжированный ряд распределения на 100 равных частей. Все вычисления аналогичны вычислениям децилей и квартилей: Нужно ли использовать квантили и какие именно, определяется, как правило, спецификой задачи анализа данных и опытом исследователя. Эксцесс случайной величины Эксцесс распределения случайной величины характеризует степень сосредоточенности её значений около центра распределения: чем более высокая такая сосредоточенность, тем выше и уже будет график плотности её распределения. Показатель эксцесса (островершинности) рассчитывается по формуле: Таким образом, для нормального распределения эксцесс равен нулю:
Рисунок. Иллюстрация островершинных и плосковершинных плотностей распределения случайных величин в сравнении с нормальным распределением.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 638; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.93.221 (0.095 с.) |
 , где
, где 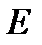 - универсальное множество событий,
- универсальное множество событий,  -
-  -алгебра событий для этого универсального множества, а
-алгебра событий для этого универсального множества, а  - вероятность (вероятностная мера на
- вероятность (вероятностная мера на  с областью определения
с областью определения  каждое множество
каждое множество 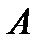 , состоящее из элементов
, состоящее из элементов 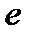 , для которых
, для которых  , входило в
, входило в 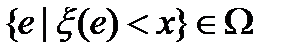 .
. , а вероятность такого случайного события – как
, а вероятность такого случайного события – как 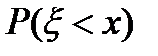 .
. является случайным событием, противоположное ему событие
является случайным событием, противоположное ему событие  тоже является случайным.
тоже является случайным.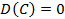 , где C – это константа, т.е. дисперсия константы равно нулю, потому что значения такой случайной величины вообще не отклоняются от её средней.
, где C – это константа, т.е. дисперсия константы равно нулю, потому что значения такой случайной величины вообще не отклоняются от её средней. т.е. дисперсия любой случайной величины всегда неотрицательна.
т.е. дисперсия любой случайной величины всегда неотрицательна. , если случайные величины независимы. Тогда дисперсия их суммы равна сумме их дисперсий.
, если случайные величины независимы. Тогда дисперсия их суммы равна сумме их дисперсий. , где a – это какое-то число. Значит, число можно выносить из под знака дисперсии с возведением этого числа в квадрат.
, где a – это какое-то число. Значит, число можно выносить из под знака дисперсии с возведением этого числа в квадрат. , где a и b – это числа, это следствие из предыдущих свойств дисперсии.
, где a и b – это числа, это следствие из предыдущих свойств дисперсии.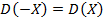 , т.е. дисперсия является чётной функцией от случайной величины – не имеет значения, вычисляется дисперсия от самой случайной величины или противоположной ей по значениям (со знаками минус). Обе эти дисперсии будут равны.
, т.е. дисперсия является чётной функцией от случайной величины – не имеет значения, вычисляется дисперсия от самой случайной величины или противоположной ей по значениям (со знаками минус). Обе эти дисперсии будут равны.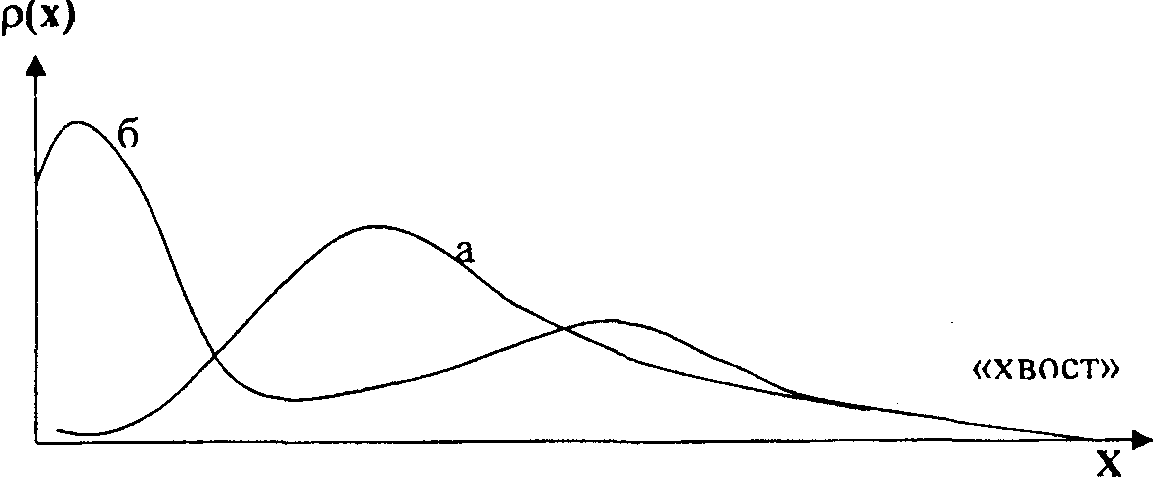
 ,
, - это мода,
- это мода, 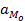 - значение начала модального интервала (его левая граница),
- значение начала модального интервала (его левая граница),  - ширина модального интервала (от левой до правой границы),
- ширина модального интервала (от левой до правой границы),  - частота модального интервала,
- частота модального интервала,  - частота интервала непосредственно предшествующего модальному, а
- частота интервала непосредственно предшествующего модальному, а  - частота интервала непосредственно следующего за модальным. Следовательно, в этой формуле мода интервального ряда представляет собой сумму значения начального уровня модального интервала и ширины отрезка, который определяется соотношением частоты ближайших к модальному интервалов.
- частота интервала непосредственно следующего за модальным. Следовательно, в этой формуле мода интервального ряда представляет собой сумму значения начального уровня модального интервала и ширины отрезка, который определяется соотношением частоты ближайших к модальному интервалов.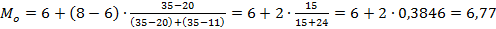 . Это, безусловно, приближённое значение моды, но в данном случае точно её значение определить невозможно. И на практике считается, что этот второй вариант определения моды для интервального ряда распределения точнее даёт её значение, чем для простого варианта с серединой интервала.
. Это, безусловно, приближённое значение моды, но в данном случае точно её значение определить невозможно. И на практике считается, что этот второй вариант определения моды для интервального ряда распределения точнее даёт её значение, чем для простого варианта с серединой интервала.
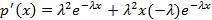 =
=  . Теперь решим уравнение
. Теперь решим уравнение 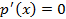 . Приравняем к нулю результат вычисления этой производной:
. Приравняем к нулю результат вычисления этой производной:  . В левой части два сомножителя больше нуля:
. В левой части два сомножителя больше нуля:  по условию задачи, а
по условию задачи, а  , потому что значения показательной функции всегда больше нуля. Получается, что нулю может равняться только последний, третий сомножитель:
, потому что значения показательной функции всегда больше нуля. Получается, что нулю может равняться только последний, третий сомножитель:  . Решая это линейное уравнение, получаем:
. Решая это линейное уравнение, получаем: 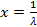 . В этой точке плотность вероятности будет иметь максимум, потому что величина
. В этой точке плотность вероятности будет иметь максимум, потому что величина  при
при  , т.е. левее
, т.е. левее  величина
величина  ,, т.е. правее
,, т.е. правее 
 . Очевидно, что для дискретных величин это уравнение не всегда имеет решение, может иметь даже бесконечное множество решений в силу ступенчатого характера функции распределения вероятностей. Графическое решение этого уравнения показано на следующем рисунке.
. Очевидно, что для дискретных величин это уравнение не всегда имеет решение, может иметь даже бесконечное множество решений в силу ступенчатого характера функции распределения вероятностей. Графическое решение этого уравнения показано на следующем рисунке.
 , это и есть медиана данного распределения. Хотя такого значения IQ=105 в данном ряду распределения нет.
, это и есть медиана данного распределения. Хотя такого значения IQ=105 в данном ряду распределения нет. , и для которого 0<p<1, потому что p – это вероятность, – это значение случайной величины, для которого функция распределения принимает значение p или имеет место «скачок» со значения меньше p до значения больше p. Иначе говоря, «квантиль порядка p» - это такое значение аргумента функции распределения случайной величины, что
, и для которого 0<p<1, потому что p – это вероятность, – это значение случайной величины, для которого функция распределения принимает значение p или имеет место «скачок» со значения меньше p до значения больше p. Иначе говоря, «квантиль порядка p» - это такое значение аргумента функции распределения случайной величины, что  . Поскольку по определению функции распределения
. Поскольку по определению функции распределения  , можно говорить, что
, можно говорить, что  , для которого вероятность
, для которого вероятность  . Для непрерывных функций распределения, как правило, существует единственная квантиль
. Для непрерывных функций распределения, как правило, существует единственная квантиль  , ведь оба эти значения определяют середину распределения:
, ведь оба эти значения определяют середину распределения:  и
и  дл квантиля
дл квантиля  .
. ,
,  ,
, 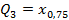 ,
,  Квартиль
Квартиль  используется крайне редко, потому что он просто характеризует всё распределение. А 1-й квартиль – это значение, ниже которого находится 25% совокупности. 2-й квартиль делит совокупность данным пополам (это совпадает с медианой), а 3-й квартиль отделяет 25% наибольших значений.
используется крайне редко, потому что он просто характеризует всё распределение. А 1-й квартиль – это значение, ниже которого находится 25% совокупности. 2-й квартиль делит совокупность данным пополам (это совпадает с медианой), а 3-й квартиль отделяет 25% наибольших значений. – это разница между 3-м и 1-м квартилями, т.е.
– это разница между 3-м и 1-м квартилями, т.е.  . Эта величина позволяет оценить разброс 50% элементов в распределении случайной величины и не учитывать влияние экстремальных элементов. У квартильного размаха
. Эта величина позволяет оценить разброс 50% элементов в распределении случайной величины и не учитывать влияние экстремальных элементов. У квартильного размаха  , что означает выполнение соотношения
, что означает выполнение соотношения  . При этом децили не совпадают с квартилями, кроме второго или медианы, когда это совпадение есть:
. При этом децили не совпадают с квартилями, кроме второго или медианы, когда это совпадение есть:  . Аналогично квартильному нередко используют децильный размах:
. Аналогично квартильному нередко используют децильный размах:  . Децильный размах в распределении доходов населения показывает, например, долю тех, кто имеет средние доходы – не бедствует, но и не является очень богатым.
. Децильный размах в распределении доходов населения показывает, например, долю тех, кто имеет средние доходы – не бедствует, но и не является очень богатым. . Процентили позволяют вычислять как квартильный размах:
. Процентили позволяют вычислять как квартильный размах: 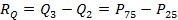 , так и децильный размах:
, так и децильный размах:  .
. , где
, где  - это центральный момент 4 порядка, а
- это центральный момент 4 порядка, а 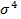 – это стандартное отклонение, возведённое в 4 степень. Поскольку степени числителя и знаменателя одинаковы эксцесс является безразмерной величиной. При этом принято за эталон отсутствия эксцесса, нулевого эксцесса, брать нормальное распределение. Но можно доказать, что для нормального распределения
– это стандартное отклонение, возведённое в 4 степень. Поскольку степени числителя и знаменателя одинаковы эксцесс является безразмерной величиной. При этом принято за эталон отсутствия эксцесса, нулевого эксцесса, брать нормальное распределение. Но можно доказать, что для нормального распределения  . Поэтому в формуле для вычисления эксцесса из этой дроби число 3 вычитается.
. Поэтому в формуле для вычисления эксцесса из этой дроби число 3 вычитается.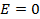 . Если эксцесс больше нуля, т.е.
. Если эксцесс больше нуля, т.е.  , то распределение более островершинное, чем нормальное. Если эксцесс меньше нуля, т.е.
, то распределение более островершинное, чем нормальное. Если эксцесс меньше нуля, т.е.  , то распределение менее островершинное, чем нормальное. Предельным значением отрицательного эксцесса является значение
, то распределение менее островершинное, чем нормальное. Предельным значением отрицательного эксцесса является значение  ; величина положительного эксцесса может быть бесконечно большой. Как выглядят графики островершинных и плосковершинных плотностей распределения случайных величин в сравнении с нормальным распределением, показано на рисунке.
; величина положительного эксцесса может быть бесконечно большой. Как выглядят графики островершинных и плосковершинных плотностей распределения случайных величин в сравнении с нормальным распределением, показано на рисунке.



