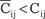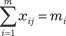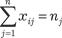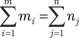Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ:  Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия ЭкологияТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
III этап. Определение переменной, выводимой из базиса
(построение цикла). Процедура построения цикла эквивалентна использова- нию условия допустимости в симплекс-методе. 1. Строится замкнутый цикл, соответствующий вводимой переменной. Он состоит из последовательности горизонталь- ных и вертикальных связанных отрезков, концами которых должны быть базисные переменные (за исключением тех кон- цов, которые относятся к вводимой в базис переменной). Для каждого базисного решения и соответствующей небазисной переменной можно построить лишь один цикл. 2. Нечетным вершинам цикла (начиная с вводимой в базис переменной) присваивается знак “+”, четным — “−” (будем на- зывать эти клетки плюсовыми и минусовыми). 3. Определяется выводимая из базиса переменная, кото- рой является одна из базисных переменных, расположенных в вершинах цикла, отмеченных знаком “−” и имеющих наимень- шее значение. 4. Формируется новое допустимое базисное решение. Для этого переменные, находящиеся в вершинах цикла, соответс- твующим образом корректируются, а именно уменьшаются или увеличиваются на величину вводимой в базис переменной в зависимости от знака вершины цикла. Описанный выше переход от одного опорного плана транс- портной задачи к другому ее опорному плану называется сдви- гом по циклу пересчета. Следует отметить, что при сдвиге по циклу пересчета число занятых клеток остается неизменным и равным (n + m − 1). Однако при определении опорного плана или в процессе решения задачи может быть получен вырожденный опорный план. Чтобы избежать зацикливания, следует соответствую- щие нулевые элементы опорного плана заменить сколь угодно малым числом ε и решать задачу как невырожденную. В опти- мальном плане такой задачи необходимо считать ε = 0. Пример 10.1. Найти квазиоптимальное решение транспор- тной задачи по методу Фогеля. Матрица транспортной задачи представлена таблицей вида:
В скобках в клетках таблицы представлены цены пере- возок. Найти план по методу Фогеля. Решение Справка Поиск квазиоптимального решения транспортной задачи по алгоритму Фогеля включает выполнение следующих шагов:
a) Для каждой строки таблицы упорядочить элементы цен перевозок cij по возрастанию. Вычислить величину так называ- емого штрафа строки как разность значений второго и первого элемента в ранжированном ряду. b) Для каждого столбца таблицы упорядочить элементы цен перевозок cij по возрастанию и вычислить величину “штра- фа столбца” аналогично шагу 1. c) Найти строку или столбец, имеющую (имеющий) на- ибольший штраф по всем штрафам строк и столбцов, а в ней (в нем) — элемент с минимальной величиной стоимости перево- зок cij. Зафиксировать индексы (i, j) этого элемента. d) Присвоить переменной xij, индексы которой соответс- твуют шагу с, наибольшее из допустимых для нее значений (с учетом ограничений задачи). e) Скорректировать величины аi и bj и вычеркнуть строку i, если оказалось, что аi = 0, или столбец j, если bj = 0. f) Проверить, все ли величины аi и bj равны нулю. Если да, то окончить вычисления; в противном случае взять в ка- честве исходной оставшуюся часть таблицы и перейти к шагу с алгоритма. 2. Вычисляем штрафы строк: Ранжированные цены в строках: Штрафы строк: (0,4; 2,7; 4,0; 4,8) 2,3 (0,6; 1,9; 3,2; 4,0) 1,3 (1,0; 1,1; 2,2; 4,6) 0,1 3. Вычисляем штрафы столбцов: Штрафы столбцов: Разности штрафов столбцов: (0,4; 0,6; 4,6) 0,2 (1,0; 3,2; 4,0) 2,2 (1,9; 2,2; 2,7) 0,3 (1,1; 4,0; 4,8) 2,9 4. Определяем максимальный штраф. Он составляет 2,9 и находится в четвертом столбце. Фиксируем элемент с наимень- шей ценой перевозок в четвертом столбце: это элемент с коор- динатами (3, 4). 5. Присвоим переменой x34 наибольшее из допустимых для нее значений 20. 6. Корректируем содержимое исходной таблицы, уменьшив запас на складе А3 на 20 т и вычеркнув четвертый столбец:
7. Вычисляем штрафы строк: Ранжированные цены в строках: Штрафы строк: (0,4; 2,7; 4,0) 2,3 (0,6; 1,9; 3,2) 1,3 (1,0; 2,2; 4,6) 1,2 8. Вычисляем штрафы столбцов: Штрафы столбцов: Разности штрафов столбцов: (0,4; 0,6; 4,6) 0,2
(1,0; 3,2; 4,0) 2,2 (1,9; 2,2; 2,7) 0,3 9. Определяем максимальный штраф. Он составляет 2,3 и на- ходится в первой строке. Фиксируем элемент с наименьшей ценой перевозок в первой строке: это элемент с координатами (1, 1). 10. Присвоим переменой x11 наибольшее из допустимых для нее значений 30. 11. Продолжая действовать таки образом, окончательно получим квазиоптимальный план перевозок:
Можно проверить, что полученное решение оказалось оп- тимальным.
10.3. Практическое решение задачи оптимального планирования Перевозки товаров различными транспортными средства- ми в ряде случаев приводят к таким нежелательным явлениям, как порожние пробеги, простои, встречные и нерациональные перевозки. Для их исключения используются методы опти- мального планирования перевозок, в частности такая экономи- ко-математическая модель, как транспортная задача. Простейшим примером транспортной задачи является задача о планировании перевозок некоторого продукта из ко- нечного числа пунктов отправления в конечное число пунктов назначения при обеспечении минимальных затрат на выполне- ние данной операции. Постановку и методику решения подобных задач рассмот- рим с использованием следующего примера: Пример 10.2. Три поставщика некоторого товара распола- гают следующими запасами: первый — 120 единиц, второй — 100 единиц, третий — 80 единиц. Товар должен быть перевезен трем потребителям: спрос первого — 90 единиц; спрос второ- го — 90 единиц; спрос третьего — 120 единиц. Известны также показатели затрат (cij) на перевозку единицы товара от каждо- го поставщика к каждому потребителю. Требуется составить оптимальный план перевозок, приводя- щий к наименьшим затратам на выполнение данной операции.
x11 x12 x13 x21 x22 x23 x31 x32 x33, в которой xij — количество единиц товара, планируемого к пе- ревозке от поставщика с номером i к потребителю с номером j. Для решения задачи исходные данные удобно свести в табл. 10.2. Таблица 10.2 Поставщики |
Возможности поставщиков |
Потребители и их спрос | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 2 | 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 90 | 90 | 120 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 120 | 7 | 6 | 4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | 100 | 3 | 8 | 5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | 80 | 2 | 3 | 7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Под планом перевозок понимается матрицаКаждую клетку таблицы пометим двойным индексом (i, j). Первый (i) — номер поставщика, второй (j) — номер потребителя. В табл. 10.2. числа 7, 6, 4 и т. д. обозначают стоимости пере-
возок cij.
Математическая постановка данной задачи имеет вид:
найти минимум целевой функции (показателя эффек-
тивности)
Z = 7х11 + 6х12 + 4х13 + 3х21 + 8х22 + 5х23 + +2х31 +3х32 + 7х33
при ограничениях:
 |
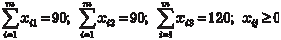Транспортная задача относится к классу задач линейно- го программирования. Решение таких задач обычно связано с
получением опорного (допустимого) плана и последующим его улучшением.
Опорный план может быть получен различными методами. Рассмотрим два из них: метод минимального элемента, или ме- тод наименьших затрат и метод “северо-западного” угла.
В соответствии с методом наименьших затрат выберем в таблице клетку, имеющую наименьший показатель затрат, т. е. клетку (3, 1). Произведем поставку в эту клетку, равную 80 еди- ницам, поскольку первому потребителю требуется 90 единиц, а у третьего поставщика в наличии лишь 80 единиц. Первому потребителю необходимо еще 10 единиц товара. Он может по- лучить их или от первого, или от второго поставщика. Так как показатель затрат в клетке (2, 1) меньше, чем в клетке (1, 1), то
|
|
записываем 10 единиц в клетку (2, 1).
Второй поставщик, отдав 10 единиц, будет располагать 90 единицами. Их можно направить второму или третьему пот- ребителю. В связи с тем, что показатель затрат в клетке (2, 3) меньше, чем в клетке (2, 2), направим их третьему потребите- лю. Недостающие 30 единиц третий потребитель получит от первого поставщика.
Оставшиеся у первого поставщика 90 единиц запишем в клет- ку (1, 2) и, тем самым, удовлетворим спрос второго потребителя.
На этом распределение можно считать законченным. При- веденную выше последовательность действий и результаты распределения иллюстрирует табл. 10.3.
Таблица 10.3
 |
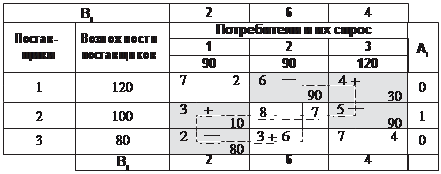Пример 10.3. Теперь решим задачу поиска опорного плана
методом “северо-западного” угла.
При этом методе не обращают никакого внимания на по- казатели затрат. Начав заполнение таблицы с клетки (1, 1) — “северо-западный” угол таблицы, последовательно ступенями спускаются вниз до клетки (3, 3). Полученный опорный план представлен в табл. 10.4.
Таблица 10.4
|
Постав- щики |
Возможности поставщиков |
Потребители и их спрос |
A i | ||||
| 1 | 2 | 3 | |||||
| 90 | 90 | 120 | |||||
| 1 | 120 | 7 | 6 | 4 3 | 0 | ||
| 90 | 30 | ||||||
| 2 | 100 | 3 | 9 | 8 | 60 | 5 | 2 |
| 3 | 80 | 2 | 11 | 3 | 10 | 7 80 | 4 |
| Bj | 7 | 6 | 3 | ||||
Получив опорный план, необходимо оценить соответству- ющую ему стоимость перевозок (показатель эффективности или целевую функцию). Для плана, полученного методом на- именьших затрат, Z = 1300 ед. Во втором случае имеем 2050 ед. Следующим этапом решения задачи, независимо от того, каким методом был найден опорный план, является последо- вательное его улучшение до получения оптимального распре-
деления.
С этой целью каждому поставщику товаров поставим в со- ответствие потенциалы А1, А2, АЗ и запишем их в дополнитель- ном столбце табл. 10.3; 10.4, а каждому потребителю — потенци- алы В1, В2, В3, которые запишем в дополнительной строке. Один из потенциалов, например А1, приравняем к нулю, а остальные найдем с использованием зависимости (решение производится для первого опорного плана):
Cij = Аi + Bj.
 |
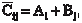Запишем данное соотношение для всех заполненных кле- ток (Xij > 0) и определим А2, А3, В1, В2, В3. Для незаполненных клеток (Xij = 0) запишем аналогичную зависимость
|
|
левую часть которой принято называть псевдостоимостью.
Условие оптимальности плана заключается в том, что для каждой свободной клетки (Xij = 0)
|
Найдем для свободных клеток разности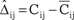 
. Посколь- ку одна из разностей, соответствующая клетке (3, 2) табл. 10.3, отрицательна, то улучшение плана начинаем именно с нее.
Заметим, что если отрицательных разностей несколько, то первой выбирается клетка, для которой разность по абсолют- ной величине больше.
Догрузим клетку (3, 2), поставив в нее знак плюс (+), и со- ставим цепь пересчета по правилу: цепь пересчета строится в виде прямоугольника, одна из вершин которого находится в свободной клетке (3, 2), а остальные — в занятых; все углы должны быть прямыми; в одной строке и в одном столбце не должно быть более двух вершин; всем вершинам приписыва- ются чередующиеся знаки (плюс — догрузить, минус — раз- грузить).
Из клеток со знаком минус (−) выбирается наименьшая ве- личина груза min (80, 90, 90) = 80 и перемещается последова- тельно по клеткам построенной цепи: 80 единиц добавляются в клетки со знаком плюс и изымаются из клеток со знаком минус. Таким образом, получаем новый план перевозок. Приме-
нив к нему рассмотренную выше методику, можно убедиться, что этот план является оптимальным.
Ниже приведена табл. 10.5, иллюстрирующая методику решения задачи (для опорного плана, полученного методом на- именьших затрат):
Таблица 10.5
| 90 | 90 | 120 | ||||
| 7 | 6 | 4 | ||||
| 120 |
| – | + | |||
|
| 10 | 110 | ||||
| 3 | 8 | 5 | ||||
| 100 | – |
| – | |||
| 90 |
| 10 | ||||
| 80 | 2 | 3 80 | + | 7 | ||
В общем случае математическая постановка транспортной задачи имеет вид
при ограничениях
|
|
|
,
т. е. возможности поставщиков равны суммарному спросу пот- ребителей. Транспортные задачи подобного вида называют за- крытыми. Задачи, для которых это условие не выполняется, представляют собой открытые задачи.
Для решения открытых задач их приводят к закрытому виду путем введения фиктивного поставщика или фиктивного потребителя с возможностями по поставке или спросом, опре- деляемыми по формуле
.
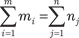В остальном методика решения задачи остается неиз- менной.
Рассмотрим пример решения открытой задачи.
Пример 10.4. Пусть требуется найти оптимальное распре- деление поставок в следующей задаче:
найти минимум целевой функции (показателя эффек-
тивности)
W(x) = 4х11 + х12 + 3х13 + 5х14 + 2х21 + 2х22 + 3х23 +
+ 7х24 + 4х31 + 4х32 + 5х33 + 3х34
 |
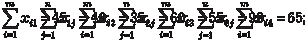при ограничениях:
xij ≥ 0.
Введем фиктивного поставщика с возможностями по пос- тавкам
| (45+35+55+65) − (40+60+90) | = 10.
Для этого исходную таблицу дополним фиктивной строкой и проведем первоначальное распределение поставок (табл. 10.6).
Таблица 10.6
| 45 | 35 | 55 | 65 | |
| 40 | 4 | 1 35 | 3 5 | 5 |
| 60 | 2 10 | 2 | 3 50 | 7 |
| 90 | 4 35 | 4 | 5 | 3 55 |
| Ф(10) | 0 | 0 | 0 | 0 10 |
Полученное распределение поставок неоптимально.
|
|
Выполнив по приведенной выше методике необходимые действия, можно установить, что для клетки (4, 3) разность Δ43
отрицательна и среди отрицательных разностей наибольшая по абсолютной величине. Следовательно, улучшение плана следует начать именно с нее. Ниже приведена соответствую- щая цепь пересчета (табл. 10.7):
Таблица 10.7
| 45 | 35 | 55 | 65 | |
| 40 | 4 | 1 35 | 3 5 | 5 |
| 60 | 2 20 | 2 | 3 40 | 7 |
| 90 | 4 25 | 4 | 5 | 3 65 |
| Ф(10) | 0 | 0 | 0 10 | 0 |
Данная таблица уже не содержит отрицательных разно- стей Δij. Следовательно, приведенное в ней распределение пос- тавок — оптимальное.
В заключение отметим, что оптимизация перевозок может осуществляться не только по затратам, но также и по другим показателям, например времени. Кроме того, следует помнить о том, что задачи линейного программирования вообще и транс- портная задача в частности в настоящее время решаются с ис- пользованием ЭВМ и соответствующего пакета прикладных программ для них.
