
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление тройных интегралов в декартовой системе координатСодержание книги
Поиск на нашем сайте
Если задан тройной интеграл от функции f (x, y, z), т. е.
 и область G расположена в системе декартовых координат 0 XYZ, то, разбив область G плоскостями, парал- лельными координатным плоскостям, получим частичные об- ласти, которые будут параллелепипедами с гранями, парал- лельными плоскостям 0 XY, 0 YZ, 0 XZ. Элемент объема в этом случае будет равен dV = dx · dy · dz и поэтому будем иметь и область G расположена в системе декартовых координат 0 XYZ, то, разбив область G плоскостями, парал- лельными координатным плоскостям, получим частичные об- ласти, которые будут параллелепипедами с гранями, парал- лельными плоскостям 0 XY, 0 YZ, 0 XZ. Элемент объема в этом случае будет равен dV = dx · dy · dz и поэтому будем иметь
. 1. Простейший случай Если пространственная область G задана неравенствами a ≤ x ≤ b; c ≤ y ≤ d; k ≤ z ≤ p; т. е. представляет собой параллеле- пипед, ребра которого параллельны осям координат, то трой- ной интеграл находится по формуле
или по одной из аналогичных, так как аргументы x,y,z могут меняться местами, так же как в двойном интеграле (см. под- разд. 5.6). Выражение, стоящее в правой части формулы (5.41) называется повторными интегралом. Заметим, что внешний интеграл соответствует внешнему дифференциалу, а внутрен- ний внутреннему. В формуле (5.41) сначала находится внутренний интеграл по переменной х при постоянных z и у, затем вычисляется средний интеграл по переменной у при постоянной z и наконец определяется внешний интеграл по переменной z. Приведем конкретный пример применения формулы (5.41). Пример 5.58.
Найти интеграл
2. Общий случай
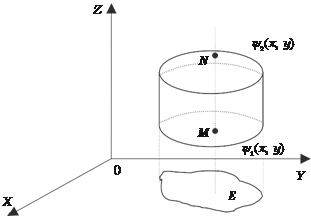
Предположим, что областью интегрирования G является тело, ограниченное снизу поверхностью ψ1(х, у), а сверху − по- верхностью ψ2(х, у), причем ψ1(х, у) ≤ ψ2(х, у) и данные функции являются непрерывными в замкнутой области Е, которая явля- ется проекцией тела на плоскость 0 ХУ (рис. 5.45). Рис. 5.45 Пусть область G будет правильной в направлении оси 0 Z, т. е. любая прямая, параллельная оси 0 Z, пересекает область не более чем в двух точках. В этом случае для любой непрерывной в области G функции f (x, y, z) будет верна формула
Формула (5.42) сводит вычисление тройного интеграла к вы- числению двойного интеграла. Сначала находится внутренний интеграл по переменной z при постоянных х и у. Нижней гра- ницей интегрирования будет аппликата точки М — точки входа прямой, параллельной оси 0 Z, в область G, т. е. ψ1(х, у), а верх- ней − аппликата точки N — точки выхода прямой из области G,
т. е. ψ2(х, у). Результат нахождения этого интеграла — функция
В том случае, если об- ласть Е ограничена линиями х = а, х = b (а < b), y = ϕ1(х), y = ϕ (х) (ϕ (х) > ϕ (х)) и дан- 2 2 1
0 a b Рис. 5.46 ные функции непрерывны на отрезке [ a, b ] (рис. 5.46), то, переходя от двойного ин- X теграла к повторному, полу- чим формулу
Если область Е ограниченна линиями у = с, у = d (c < d), x =
. (5.44)
Если область G является сложной, то ее надо разбить на конечное число правильных областей, к которым можно при- менить формулы (5.43) и (5.44). Y d c 0 a b Рис. 5.47 Аналогичные формулы можно получить и для случаев, когда область G будет правиль- ной в направлении осей 0 Х и 0 У.
Найти тройной интеграл
X z = 0 и плоскостью х + у + z = 1 (рис. 5.48).
Рис. 5.48 В этом случае интегрирование по z совершается от z = 0 до z = 1 − x − y. Поэтому, обозначив проекцию области G на плос- кость 0 ХУ через Е, получим по формуле (5.43):
Аналогичный результат можно получить, используя фор- мулу (5.44), т. е.
Задачи для самостоятельного решения 1. Методом непосредственного интегрирования найти ин- тегралы: 1.1.
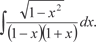
2. Найти интегралы, использовав метод замены переменной: 2.1.
3. Найти интегралы, использовав метод интегрирования по частям: 3.1. 3.3. 4.
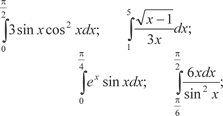 Вычислить определенные интегралы: Вычислить определенные интегралы:
5.
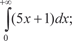 5.2. 5.2. 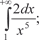
5.3. 6. Найти объем тела, полученного вращением вокруг оси 0х криволинейной трапеции, ограниченной функцией ху =4 и прямыми х = 1, х = 4 и осью 0 х.
7.
криволинейной трапеции, ограниченной функцией и прямыми у = ±2 b. 8. Найти объем тела, полученного вращением вокруг оси 0 х криволинейной трапеции, ограниченной линиями 2 у 2 = х 3, х = 4. 9. Найти объем тела, полученного вращением вокруг оси 0 х криволинейной трапеции, ограниченной линиями у = х 3, х = 0, у = 8. 10. Фигура, ограниченная одной дугой синусоиды у = sin x и осью 0 х, вращается вокруг оси 0 х. Найти объем тела вращения. 11. Найти площадь фигуры, ограниченной кривой у = х 3, прямой у = 10 и осью 0 у. 12. Вычислить площади фигур, ограниченных линиями: 12.1. у = х 2, у 2 = х; 12.2. у = ln x, x = e, y = 0; 12.3. y 3 = x 2, y = 1; 12.4. y = x 2, y = 2 x 2 − 1 13. Вычислить длину дуги полукубической параболы
14. Найти длину дуги кривой от х = 0 до х = 1. 15. Найти длину дуги кривой от у = 0 до у = 3. 16. Определите длину окружности х 2 + у 2 = 25. 17. Используя формулу прямоугольников, вычислить ин- теграл 18. Используя формулу трапеции, вычислить интеграл 19. Используя формулу Симпсона вычислить интеграл
20. Вычислить двойные интегралы:

20.2.
21. Вычислить интеграл 21.1. х = 2, х = 3, у = -1, у = 5; 21.2. х = 0, х = 5, у = -2, у = 2. 22. 22.3. 22.4.
22.5. 22.6. 23. Исследовать на сходимость несобственные интегралы. 23.1. 23.3. 24. Расставить пределы интегрирования в двойном интег- рале 25.
26. Вычислить двойной интеграл ограничена линиями: у 2 = х, х = 0, у = 1. 27. Вычислить двойной интеграл 28. Найти объем тела, ограниченного поверхностями: Z = = x 2 + y 2 + 1, Z = 5. 29. Найти площадь фигуры, ограниченной линией: (х 2 + + у 2)2 = = 4(х 2 − у 2). 30. Найти площадь фигуры, ограниченной линиями: r = 4(1 + + cosϕ), r = 4cosϕ. 31.
31.1. ; 31.2. 32. Найти тройной интеграл
33. Найти неопределенные интегралы: 33.1. 33.2. 33.3. Вопросы для самопроверки 1. Интеграл какого вида называется интегралом от диффе- ренциального бинома? 2. В каких случаях интеграл от дифференциального бино- ма можно выразить в элементарных функциях? 3. Какая функция называется первообразной? 4. В чем состоит суть метода интегрирования по частям? 5. В чем состоит суть метода замены переменной? 6. Каков геометрический смысл определенного интеграла? 7. В чем состоит суть метода замены переменной в опреде- ленном интеграле? 8. Вывести формулу для объема тела вращения. 9. В каких случаях применяют приближенные методы ин- тегрирования? 10. В чем заключается суть признаков сходимости несобс- твенных интегралов с бесконечными пределами? 11. В чем состоит теорема существования двойного интег- рала? 12. Как «берутся» интегралы от иррациональных функ- ций?
13. С помощью каких подстановок решаются интегралы вида 14. Дайте определение несобственного интеграла от раз- рывной функции на конечном участке интегрирования. 15. Как осуществляется замена переменной в двойном ин- теграле? 16. Как находится масса неоднородного тела по заданной плотности? 17. Сформулировать теорему существования тройного ин- теграла. 18. Как находятся тройные интегралы в декартовой систе- ме координат?
Глава 6. НЕКОТОРЫЕ СВЕДЕНИЯ
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 166; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.117.234 (0.011 с.) |

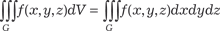
 (5.41)
(5.41)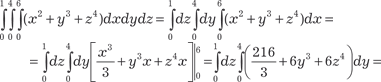

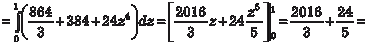

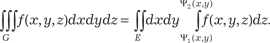 (5.42)
(5.42)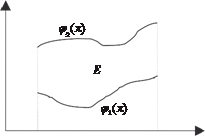 Y двух аргументов х и у.
Y двух аргументов х и у.
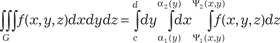
 Пример 5.59.
Пример 5.59.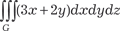 , если об- ласть G ограничена координат- ными плоскостями х = 0, у = 0,
, если об- ласть G ограничена координат- ными плоскостями х = 0, у = 0,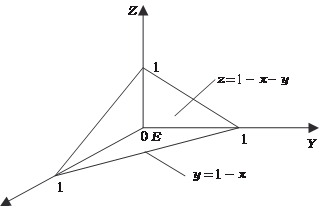 X
X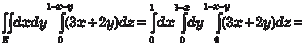

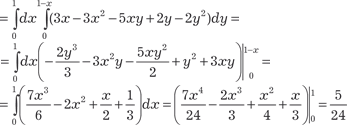 .
.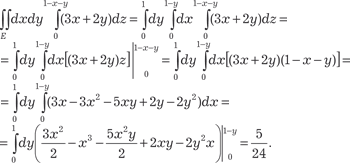
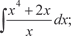 1.2.
1.2. 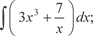

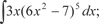 2.2.
2.2. 
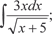
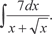
 3.2.
3.2. 
 3.4.
3.4. 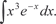
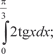
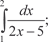

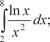
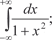 5.4.
5.4. 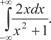

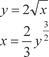 у 2 = х 3, отсекаемой прямой х = 5.
у 2 = х 3, отсекаемой прямой х = 5. , приняв n = 10.
, приняв n = 10.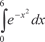 , приняв n = 10.
, приняв n = 10.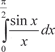 , приняв n = 10.
, приняв n = 10.
 , если область интег- рирования В ограничена линиями:
, если область интег- рирования В ограничена линиями: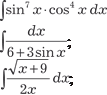
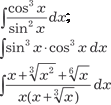 Найти неопределенные интегралы: 22.1.; 22.2.
Найти неопределенные интегралы: 22.1.; 22.2. ; 23.2.
; 23.2. 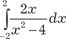 ;
;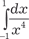 ; 23.4.
; 23.4. 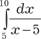
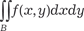 , если В — круговой сектор ОМС с центром в точке О(0; 0), у которого концы дуги М(1; 1), С(-1; 1).
, если В — круговой сектор ОМС с центром в точке О(0; 0), у которого концы дуги М(1; 1), С(-1; 1).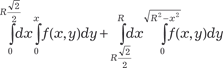
 , если область В
, если область В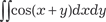 , если об- ласть В ограничена линиями: х = 0; у = π; у = х.
, если об- ласть В ограничена линиями: х = 0; у = π; у = х.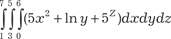
 .
. , если область интегрирования ограничена координатными плоскостями и плоскостью x + y + z = 1.
, если область интегрирования ограничена координатными плоскостями и плоскостью x + y + z = 1.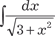 ;
; ;
;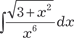 .
. ?
?


