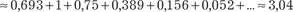Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные свойства степенных рядовСодержание книги
Поиск на нашем сайте 1. Если степенной ряд не является всюду расходящимся, то его сумма непрерывна в каждой точке области сходимости. 2. Степенной ряд внутри его области сходимости можно интегрировать почленно, так что если + (x - x) + (x - x)2 + … + (x - x) n + … = S (x), x E, 0 1 0 2 0 n 0
3. Степенной ряд внутри его интервала сходимости можно дифференцировать почленно, так что если
то
Это свойство сохраняет силу и для конца интервала сходи- мости, если только последний ряд на этом конце сходится. 4. Если степенной ряд 0 + 1(x - x 0) + 2(x - x 0)2 + … + n (x - x 0) n + … не является всюду расходящимся, то его сумма S (x) имеет внутри интервала сходимости производные всех порядков. При этом
Разложение функций в степенные ряды
Если функция f (x) имеет производные всех порядков при x = x 0, то степенной ряд
(7.8)
который часто называют рядом Маклорена. Для того чтобы ряд (7.8) сходился к функции f (x), необхо- димо и достаточно, чтобы Приведем теорему, которая позволяет устанавливать, стре- мится ли R n (x) к нулю при неограниченном возрастании n или нет, т. е., разлагается ли функция f (x) в ряд Тейлора или нет. Теорема 7.3.
где заключено между x 0 и x (см. гл. 4). Приведем разложения в степенной ряд некоторых функций:
Некоторые приложения степенных рядов Приближенное вычисление определенных интегралов Пусть необходимо найти интеграл разложение в ряд Тейлора или Маклорена. Если интеграл функциях, то полученный ряд может служить выражением для неэлементарной функции F (x) через элементарные степенные функции. Выражение это будет бесконечным.
0,1. Пример 7.13.
Данный интеграл является “неберущимся”, поэтому раз-
ложим функцию ex в ряд Маклорена (это разложение было про- ведено в подразд. 7.3). Получим:
.
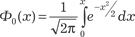 , которую называют нормирован- ной функцией Лапласа. Интеграл, которым выражается эта функция, является “неберущимся”. Поэтому разложим по- дынтегральную функцию , которую называют нормирован- ной функцией Лапласа. Интеграл, которым выражается эта функция, является “неберущимся”. Поэтому разложим по- дынтегральную функцию  в ряд, использовав разложение в ряд, использовав разложение
в ряд Маклорена функции e x, подставив туда вместо x . Тогда получим:
Полученный нами ряд сходится на всей числовой оси, схо- дится быстро, поэтому значения нормированной функции Лап- ласа удобно вычислять. Заметим, что для нахождения значе- ний функции Φ0(x) составлены таблицы.
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 150; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.007 с.) |

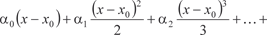
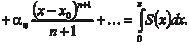
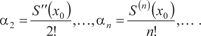
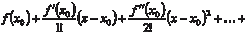

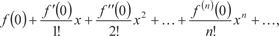 (7.9)
(7.9) , где R n (x) — остаточный член ряда Тейлора.
, где R n (x) — остаточный член ряда Тейлора.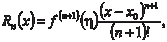

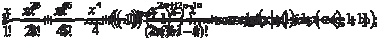
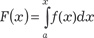 и известно разложение подынтегральной функции в ряд Тейлора или Мак- лорена, а верхний и нижний пределы данного интеграла лежат внутри интервала сходимости (- R; R). В этом случае можно интег- рировать ряд поэлементно. Получим ряд Тейлора или Маклорена для функции F (x), который имеет тот же радиус сходимости, что и ряд для подынтегральной функции f (x). Если интеграл
и известно разложение подынтегральной функции в ряд Тейлора или Мак- лорена, а верхний и нижний пределы данного интеграла лежат внутри интервала сходимости (- R; R). В этом случае можно интег- рировать ряд поэлементно. Получим ряд Тейлора или Маклорена для функции F (x), который имеет тот же радиус сходимости, что и ряд для подынтегральной функции f (x). Если интеграл  выражается через элементарную функцию F (x), то находим ее
выражается через элементарную функцию F (x), то находим ее является “неберущимся”, т. е. не выражается в элементарных
является “неберущимся”, т. е. не выражается в элементарных