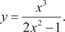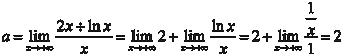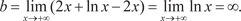Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производная по направлению и градиентСодержание книги
Поиск на нашем сайте Предположим, что в каждой точке А некоторой области D задано значение скалярной физической величины W (темпера- тура, давление, влажность и т. п.). Тогда W называется скаляр- ной функцией точки и записывается так W = W (A). Если в об- ласти D задана скалярная функция точки W (A), то говорят, что в этой области задано скалярное поле. Если скалярное поле не зависит от времени, оно называ- ется стационарным. В противном случае поле будет нестацио- нарным, т. е. будет зависеть не только от точки А, но и от вре- мени t. В гиперпространстве, в котором задано поле W = W (x 1, x 2, …, x n) возьмем точку А (x 1, x 2, …, x n) и найдем скорость изме- нения функции при движении точки А в направлении некото- рого вектора Приращение W, получаемое при переходе от точки А в точку А 1, по направлению W = W(x 1 + x 1, x 2 + x 2, …, x n + x n) - W(x 1, x 2, …, x n). Тогда Производной от функции W (x 1, x 2, …, x n) в точке А (x 1, x 2, …,
x n) по направлению  называется предел называется предел
То есть производная характеризует скорость изменения функции по данному направлению.
В курсах математического анализа доказывается (см., на- пример, [9, 42]), что Пример 4.12. Найти производную функции
в точке A (0, 1, 2, 1) по направлению к точке A 1(2, 0, 1, 3) Находим направляющие косинусы вектора cos 1 = 0,632; cos 2 = -0,316; cos 3 = -0,316; cos 4 = 0,632. Далее определяем частные производные исходной функ- ции W и их значения в точке А, т. е.
Затем вычисляем искомую производную по направлению Знак минус говорит о том, что функция в заданном направ- лении убывает.
или
где Теперь формулу для производной по направлению можно переписать в виде скалярного произведения grad W на единич- ный вектор
где — угол между вектором grad W и направлением Из последней формулы видно, что dW / d достигает своего максимального значения в том случае, когда = 0. Поэтому на- правление градиента совпадает с направлением направление скорейшего возрастания функции. А наибольшая скорость изменения функции W в точке А равна:
Пример 4.13. Найти наибольшую скорость возрастания функции
Вначале находим частные производные Затем получаем
и вычисляем нец, находим наибольшую скорость возрастания функции |grad W (A)| = 109,2.
Некоторые приложения дифференциального исчисления Формула Тейлора
(4.1)
(4.2)
Через R n (x) обозначим разность значений данной функции y = f (x)и многочлена, находимого по формуле (4.2), т. е. R n (x) = = f (x) − P n (x).
(4.3)
где R n (x) — остаточный член, который может быть записан в разных формах. Приведем так называемую форму Лагранжа, которая имеет вид:
Здесь [ x, x 0] и ее можно представить в виде = x 0 +
+ (x - x 0), где 0 < < 1. Тогда формула для остаточного члена примет вид: А формула
называется формулой Тейлора для функции y = f (x).
(4.6)
Здесь 0 < <1, а формулу (4.6) часто называют формулой Маклорена. Теперь найдем разложение функции y = ex по фор- муле (4.6). f (x) = ex; f (0) = 1; f (x) = ex; f (0) = 1; f (x) = ex; f (0) = 1, …, f (n)(x) = ex; f (n)(0) = 1. Эти данные подставляем в формулу (4.6) и получаем:
Если | x | 1, то взяв n = 8, найдем оценку остаточного члена
Здесь верны первые четыре знака после запятой, так как ошибка не превосходит числа или 10-5. Заметим, что какое бы ни было х, остаточный член при n →, т. е.
ложения, по формуле (4.6) получим ex с любой необходимой сте- пенью точности. Правило Лопиталя Данное правило помогает раскрывать неопределенности вида: Теорема 4.5 Лопиталя. Пусть функции f (x) и (x) при x → x 0 или x → совместно стремятся к нулю или к бесконеч- ности. Если отношение производных этих функций имеет пре- дел, то отношение самих функций тоже имеет предел, который равен пределу отношения производных, т. е.
Теперь рассмотрим конкретные примеры применения это- го правила. Пример 4.14.
Ранее мы сводили этот предел ко второму замечательно- му пределу и пользовались тем, что ln x является непрерывной функцией. Заметим, что простота взятия данного предела ка- жущаяся, так как дифференцирование функций само опира- ется на знание пределов.
Пример 4.16.
Заметим, что если производные числителя и знаменателя одновременно стремятся к нулю или к бесконечности можно применять правило Лопиталя еще раз, а в случае необходимос- ти и далее.
Пример 4.19. Формулы (4.7) и (4.8) справедливы только в том случае, если предел, стоящий справа (конечный или бесконечный), су- ществует. Приведем пример, когда отношение функций имеет предел, а отношение их производных не стремится ни к какому пределу.
А предел производных равен:
При x → этот предел колеблется между 0 и 2 и поэтому не имеет предела. То есть к данному примеру правило Лопита- ля применить нельзя, оно не является универсальным.
При помощи правила Лопиталя можно раскрывать другие неопределенности, например: Эти случаи сводятся к рассмотренным нами неопределен- ностям Рассмотрим некоторые примеры.
Это случай 0 ·.
исходный предел к случаю
Теперь можно применить правило Лопиталя Пример 4.22.
т. е., имеем случай −. Исходный предел преобразуем к виду
Пример 4.23.
 , т. е., имеем случай 1 . Рассмотрим предел , т. е., имеем случай 1 . Рассмотрим предел
леднему пределу применимо правило Лопиталя. Поэтому исходный предел
Пример 4.24.
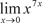 , т. е. имеем случай 00. , т. е. имеем случай 00.
Рассмотрим предел , т. е.
пришли к случаю  . Теперь к последнему примеру применяем правило Лопиталя . Теперь к последнему примеру применяем правило Лопиталя
Поэтому исходный предел равен
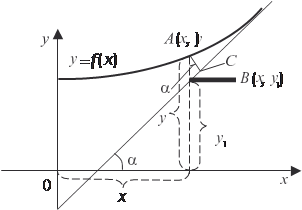
Асимптоты Прямая L называется асимптотой графика функции y = f (x), если расстояние от переменной точки А функции до этой пря- мой при удалении точки А в бесконечность стремится к нулю (рис. 4.5).
Рис. 4.5 Различают вертикальные асимптоты (параллельные оси 0 у) и наклонные. Сначала рассмотрим вертикальные асимптоты. Из определения асимптоты следует, что если
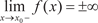 , или , или 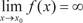 , ,
то прямая x = x 0 является асимптотой функции y = f (x) и на- оборот, если прямая x = x 0 есть асимптота кривой y = f (x), то существуют указанные выше пределы.
  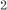 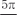 
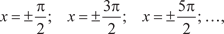
Рис. 4.6
Теперь рассмотрим наклонные асимптоты. Предположим, что функция y = f (x) имеет наклонную асимптоту y = ax + b (рис. 4.7). Рис. 4.7 Нам нужно найти коэффициенты a и b. Точка А (х, у) при- надлежит функции y = f (x), а точка В (х, y 1) — асимптоте. Дли- на отрезка АС — это расстояние от точки А до асимптоты и по условию
Обозначим через угол наклона асимптоты к положитель- ному направлению оси 0 х и из АВС найдем так как
так как (AB) = | y - y 1| = | f (x) - ax - b |, то (4.10) принимает следу- ющий вид:
Следовательно, если y = ax + b есть асимптота, то выпол- няется (4.11) и, наоборот, если при коэффициентах a и b выпол-
няется (4.11), то прямая y = ax + b является асимптотой. Теперь найдем коэффициенты a и b. Из (4.11) получаем Так как x → +, то
а так как b есть число, то 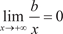 , поэтому получаем , поэтому получаем
или Получив a, находим b по формуле
Следовательно, если y = ax + b является асимптотой, то a и b находятся по формулам (4.12) и (4.13). Если хотя бы один из пределов (4.12) или (4.13) не существует, то функция y = f (x) наклонной асимптоты не имеет. Все приведенные рассуждения справедливы и при x → -. Так как асимптотическое изменение функции может быть раз- личным при стремлении х к положительной и отрицательной бесконечности, то надо раздельно рассматривать случаи x → - и x → +. Если существует асимптота в первом случае, то ее на- зывают левосторонней, а во втором случае — правосторонней. Если при x → - и x → + пределы (4.12) и (4.13) совпадают, то левосторонняя и правосторонняя асимптоты являются час- тями одной и той же прямой. Заметим, что если функция дробно-рациональная, то при нахождении a и b сразу можно рассматривать произвольное стремление к бесконечности. Рассмотрим примеры нахождения наклонных асимптот. Пример 4.25.
Так как данная функция дробно-рациональная, то сразу рассматриваем произвольное стремление х к
Пример 4.26.
y = 2x + ln x. (по правилу Лопиталя)
Из последнего равенства следует, что исходная функция наклонной асимптоты не имеет.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 240; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.01 с.) |

 . Этот вектор начинается в точке А, а косинусы углов между ним и координатными осями Х 1, Х 2, …, Х n (направ- ляющие косинусы) равны: cos 1, cos 2, …, cos n.
. Этот вектор начинается в точке А, а косинусы углов между ним и координатными осями Х 1, Х 2, …, Х n (направ- ляющие косинусы) равны: cos 1, cos 2, …, cos n. равно:
равно: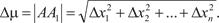
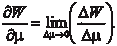
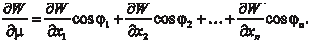
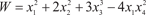
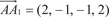 :
: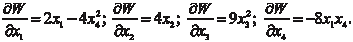
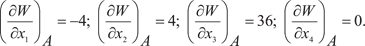
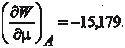
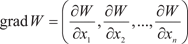
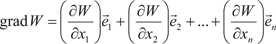 ,
, = (1, 0, …, 0);
= (1, 0, …, 0);  = (0, 1, …, 0) …
= (0, 1, …, 0) …  = (0, 0, …, 1).
= (0, 0, …, 1). = (cos 1, cos 2, …, cos n), т. е.
= (cos 1, cos 2, …, cos n), т. е. или
или 
 .
.
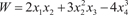 в точке А (1, 2, -1, 3).
в точке А (1, 2, -1, 3).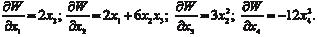
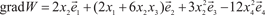
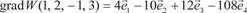 и, нако-
и, нако-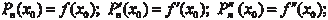
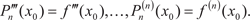
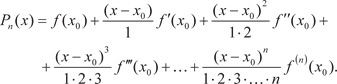
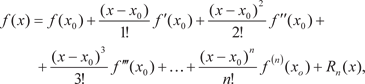
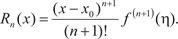 (4.4)
(4.4)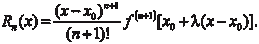
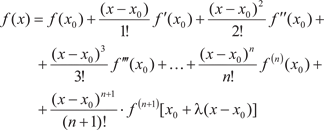
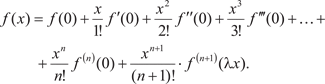
 , где 0 < <1.
, где 0 < <1.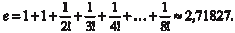
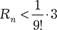
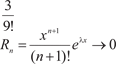
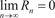
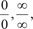 его суть выражается теоремой.
его суть выражается теоремой. (4.7)
(4.7)
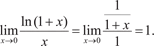
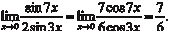
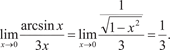
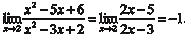
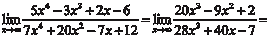

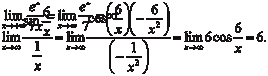


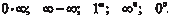
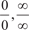 .
.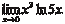
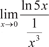
 .
.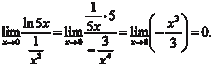
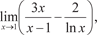
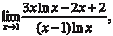
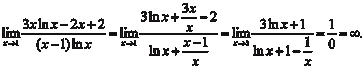

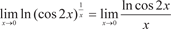
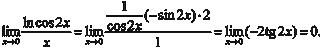


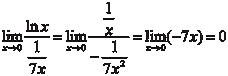
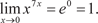




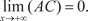 (4.9)
(4.9)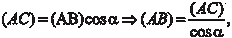
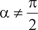 и = const, то в силу (4.9) имеем
и = const, то в силу (4.9) имеем
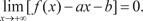 (4.11)
(4.11)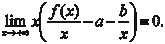
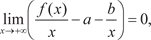
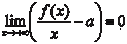
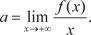 (4.12)
(4.12)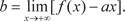 (4.13)
(4.13)