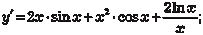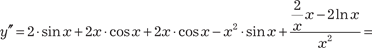Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производные основных элементарных функций
(ax) = ax ln a; (ex) = ex;
(sin x) = cos x; (cos x) = − sin x;
Дополним таблицу производных производными от гипер- болических и обратных гиперболических функций, которые не являются основными элементарными функциями, но часто ис- пользуются в различных приложениях.
К гиперболическим функциям относятся гиперболические синус (sh x), косинус (ch x) и тангенс (th x), которые находятся по формулам: Все эти функции определены на множестве действитель- ных чисел (R) и связаны между собой следующими соотноше- ниями: ch2 x - sh2 x = 1; ch2 x = ch2 x + sh2 x; sh2 x = 2sh x ch x;
Функции, обратные sh x, ch x, th x, являются обратными ги- перболическими функциями и обозначаются Arсh x (ареа-ко- синус гиперболический), Arsh x (ареа-синус гиперболический), Arth x (ареа-тангенс гиперболический):
Производные гиперболических и обратных гиперболичес- ких функций находятся по формулам: Правила дифференцирования 1. Производная алгебраической суммы функций: (f 1 (x) ± f 2 (x) ± … ± f n (x)) = f 1 (x) ± f 2 (x) ± … ± f n (x); 2. Производная произведения функций: (f 1 (x) · f 2 (x)) = f 1 (x) · f 2 (x) + f 1 (x) · f 2 (x). Исходя из этого правила для трех функций, получим, (f 1 (x) · f 2 (x) · f 3 (x)) = (f 1 (x) · f 2 (x)) · f 3 (x) + f 1 (x) · f 2 (x) · f 3 (x) = = f 1 (x) · f 2 (x) · f 3 (x) + f 2 (x) · f 1 (x) · f 3 (x) + f 3 (x) · f 1 (x) · f 2 (x); 3.
Производная частного двух функций: 4. Производная сложной функции. Сформулируем теорему.
Теорема 4.3. Производная сложной функции равна про- изводной заданной функции по промежуточному аргументу, умноженной на производную этого аргумента по независимой переменной, т. е. если y = f (u), a u = (x) и y = f ((x)), то согласно данной теореме Аналогично выводится формула при любом числе проме- жуточных аргументов, т. е. производная сложной функции рав- на произведению производных от функций ее составляющих. Например, найдем производную функции y = cos2 4 x. y = 2cos 4 x · (−sin 4 x) · 4 = −8cos 4 x · sin 4 x = −4sin 8 x; 5.
или
т. е. производные от взаимно обратных функций обратны по ве- личине. В качестве примера найдем производную функции
Примеры нахождения производных
Прежде чем найти производную от заданной функции пе- рейдем к другому основанию и найдем производную исходной функции по правилу производной частного.
Пример 4.2. y = x sin x.
Данная функция называется сложной показательной функ- цией. Чтобы найти производную от такой функции прологариф- мируем ее левую и правую части, а затем продифференцируем полученные выражения, помня, что у есть функция от х Дадим понятие о дифференциале функции. Если задана непрерывная функция y = f (x), имеющая про- изводную где (x) — бесконечно малая величина при x → 0. Далее получаем: y = f (x) · x + (x) · x. Дифференциалом (от латинского слова differentia — раз- ность) функции называется главная часть приращения этой функции, линейная относительно приращения аргумента х, т. е. dy = f (x) · x.
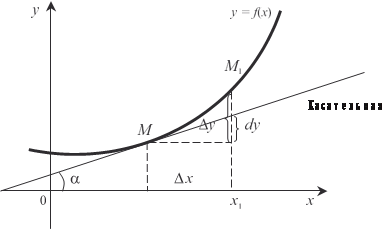
Рис. 4.3 Дифференциал функции геометрически изображает- ся приращением ординаты касательной, проведенной в точке М (х,у) при данных значениях х, х. Рассмотрим функцию у = х. Для нее получим, что dy = x, а так как у можно заменить на х по условию, то имеем dx = x. Следовательно, дифференциал функции равен dy = y dx. Отсюда следует формула:
Дадим понятие о производной второго порядка. Предполо- жим, что нам задана функция y = f (x) имеющая производную y = f (x).
Эта производная также является функцией и если она дифференцируема, то от нее можно взять производную. Она будет называться производной второго порядка: Например, найдем вторую производную функции. Пример 4.3. y = 3 x 2 + sin3 x. y = 6 x + 3sin2 x · cos x. y = 6 + 3(2sin x · cos2 x − sin3 x). С помощью первой и второй производных можно исследо- вать функцию на экстремум (max, min), находить точки пере- гиба и участки выпуклости и вогнутости функции.
Производная второго порядка  также является функцией, и производная от нее будет называться производ- ной третьего порядка от исходной функции и обозначаться сле- дующим образом: также является функцией, и производная от нее будет называться производ- ной третьего порядка от исходной функции и обозначаться сле- дующим образом:
Производная от производной третьего порядка называет- ся производной четвертого порядка от исходной функции и обо- значается так:
. Производные четвертого, пятого и высших порядков обоз- начаются либо y (4), y (5), …, либо
Например, найдем производную третьего порядка для функции y = x 2 · sin x + ln2 x.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 229; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.172.146 (0.014 с.) |
 (xn) = nxn -1;
(xn) = nxn -1;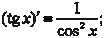
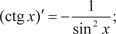
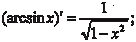

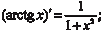

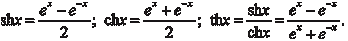

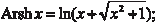
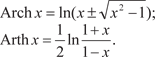
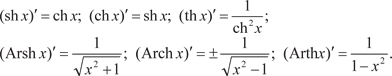



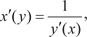
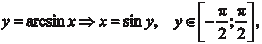
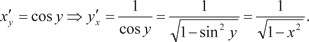


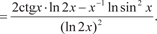
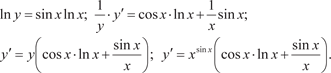
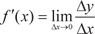 , то:
, то: 

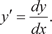
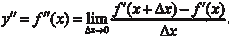
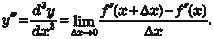
 и т. д.
и т. д.
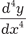 ,
, 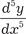 , …, либо y IV, y V, ….
, …, либо y IV, y V, ….