
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Некоторые сведения о векторахСодержание книги
Поиск на нашем сайте Цифровые данные, используемые в экономике, можно представить в виде списков чисел, каждое из которых имеет определенный смысл. Например, списки цен различных товаров в магазинах, объемы продукции разных видов, выпущенных каким-либо предприятием за год и т. д. В математике такие упорядоченные списки чисел называют векторами. Дадим определение n-мер- ного вектора (n = 1, 2, ….). Упорядоченный набор n чисел x 1, х 2, х 3, …, х n называется n - мерным вектором. Мы будем обозначать векторы заглавными буквами со стрелками над ними, т. е.
Два n -мерных вектора называются равными, если их соот- ветствующие координаты равны, например:
Вектор, все координаты которого нули, называется ноль- вектором и обозначается Алгебраической суммой двух n -мерных векторов
называется вектор
Произведением действительного числа k на n -мерный век- тор
Множество n -мерных векторов, для которых определе- ны действия алгебраического сложения (2.21) и умножения на число (2.22), называют n -мерным векторным пространством и обозначают Rn (в случае n = 1 оно совпадает с множеством действительных чисел R). В случае n = 2 и n = 3 имеем соответственно двумерное (R 2) и трехмерное (R 3) векторные пространства, а двумерные и трехмерные вектора имеют геометрическую интерпретацию: они изображаются направленными отрезками на плоскости и в пространстве. Пусть в Rn заданы вектора
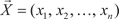 , , 
Приведем свойства линейных действий векторами: 1)
3) 4)
6) 7)
9) Длина (норма) вектора
(2.23)
Например, задан вектор
Введем понятие скалярного произведения в действитель- ном пространстве Rn. Скалярным произведением двух векторов
 = (у 1, у 2, …, у n) = (у 1, у 2, …, у n)
в R n (х R, у R, i i
(2.24)
где есть угол между n -мерными векторами
 и и  равен равен
(2.26)
 и и  равен, то скалярное произведение этих векторов равно нулю, т. е. равен, то скалярное произведение этих векторов равно нулю, т. е.
Пример 2.10. Например, заданы векторы
По формуле (2.26) получим ∧
 Скалярное произведение в пространстве Rn обладает сле- дующими свойствами: Скалярное произведение в пространстве Rn обладает сле- дующими свойствами:
1) (при этом равенство нулю будет только в том случае, если ); 2) 3) Здесь Пространство Rn, в котором введено понятие скалярно- го произведения по формуле (2.24), называется евклидовым n -мерным пространством.
Векторное произведение Введем новое действие над векторами — векторное про- изведение. При этом будем считать, что в трехмерном про- странстве задана декартова система координат. Напомним, что декартова прямоугольная система координат в пространс- тве определяется заданием линейной единицы для измерения длин и трех пересекающихся в одной точке взаимно перпенди-
а) , где α — угол между векторами
 , ,  , ,  приведены к общему началу, приведены к общему началу,
то вектор должен быть направлен так, чтобы из его кон- ца кратчайший поворот вектора
Рис. 2.2 Приведем свойства векторного произведения: 1. Если В данном случае α = 0° или α =180°, а синус α в обоих слу- чаях равен нулю. 2. Если векторное произведение векторов 3. Если векторы Из данного свойства следует, что векторное произведение можно записать в виде:
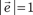 , а его расположение видно из рис. 2.3. , а его расположение видно из рис. 2.3.
Рис. 2.3 4. 5. Свойство сочетательности по отношению к скалярному множителю k:
 . .
6. Распределительное свойство относительно сложения:
Приведем без доказательства теорему, позволяющую на- ходить векторное произведение двух векторов, если заданы их координаты.
 Теорема 2.4. Если заданы координаты векторов Теорема 2.4. Если заданы координаты векторов  и и  : :
= (x 1, y 1, z 1), = (x 2, y 2, z 2), то векторное произведение вектора
(2.29)
Х Рис. 2.4 Рассмотрим некоторые задачи на применение векторного произведения. Пример 2.11.
 = (2, 5, 7); = (2, 5, 7);  = (1, 2, 4). Надо найти площадь треуголь- ника, построенного на этих векторах. Обозначим искомую пло- щадь S тр. и воспользуемся свойством 3. Получим = (1, 2, 4). Надо найти площадь треуголь- ника, построенного на этих векторах. Обозначим искомую пло- щадь S тр. и воспользуемся свойством 3. Получим  = S пар, где S пар — площадь параллелограмма, построенного на векто- = S пар, где S пар — площадь параллелограмма, построенного на векто-
рах  и и  . Из элементарной геометрии известно, что . Следовательно, получаем по формуле (2.28) . Из элементарной геометрии известно, что . Следовательно, получаем по формуле (2.28)
Пример 2.12. Дано: координаты вершины треугольника АВС: А (4, -14, 8); В (2, -18, 12); С (12, -8, 12). Надо найти длину его высоты, опу- щенной из вершины С на сторону АВ. Обозначим: площадь треугольника АВС через S тр, искомую высоту через h c. Из элементарной геометрии известно, что
где
,
 — модуль векторного произведения векторов — модуль векторного произведения векторов  и и
. Сравнивая обе формулы, получаем
Находим = (-2, -4, 4);
И окончательно получаем
Смешанное произведение
, называется число, которое равно векторному произведению
Выполняются следующие равенства .
Теорема 2.5. Смешанное произведение равно объему параллелепипеда, построенного на векторах ,, Если же векторы Приведем свойства смешанного произведения. 1. 2.
4. где R — множество действительных чисел.
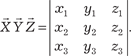
 , ,  , , 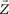 заданы своими коорди- натами, т. е. = (х 1, y 1, z 1); = (х 2, y 2, z 2); = (х 3, y 3, z 3), их сме- шанное произведение находится по формуле заданы своими коорди- натами, т. е. = (х 1, y 1, z 1); = (х 2, y 2, z 2); = (х 3, y 3, z 3), их сме- шанное произведение находится по формуле
(2.30)
 , ,  , , 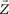 , вычисляется по формуле , вычисляется по формуле
(2.31)
В формуле (2.31) знак берется одинаковым со знаком опре- делителя. Теперь приведем конкретный пример применения сме- шанного произведения. Пример 2.13. Дано: Надо доказать, что заданные векторы компланарны.
Из теоремы 2.5 следует, что если векторы  , ,  , , 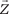 компла- нарны, то их смешанное произведение равно нулю, т. е. компла- нарны, то их смешанное произведение равно нулю, т. е.
Далее используем формулу (2.30) и получим
При решении определителя вынесли общие множители третьего столбца и второй строки, затем умножили первую строку на (-3) и сложили со второй. После этого умножили пер- вую строку на (-10) и сложили с третьей, а затем разложили получившийся определитель по элементам первого столбца. После этого вынесли общий множитель второго столбца. Так как при решения определителя мы получили ноль, то доказано, что заданные векторы
Базис пространства Rn
Пусть в пространстве Rn задано n векторов:
Базисом пространства Rn называется любая система из n линейно независимых векторов этого пространства.
Заметим, что в пространстве R 2 базис составляют два не- коллинеарных вектора, а в пространстве R 3 — три некомпла- нарных вектора.
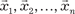 называется линейно незави- симой, если выполняется равенство называется линейно незави- симой, если выполняется равенство
, (2.32) В том случае, если хотя бы одно значение k i, в фор- муле (2.32) не равно нулю, система векторов Заметим, что система векторов, которая содержит ноль- вектор, всегда линейно зависима. Перепишем выражение (2.32), поставив вместо векторов
. (2.33)
. (2.34)
Полученная система однородных уравнений (2.34) всегда совместна.
, (2.35)
то система (2.34) имеет единственное решение k 1 = k 2 = … = k n = 0, а это значит, что векторы Пример 2.14. Составлют ли векторы = (0, 1, 0, …, 0); …;
Видно, что данный определитель не равен нулю, поэтому векторы
.
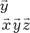
 = (0, 3, -1); = (5, 16, 10). Показать, что векто- = (0, 3, -1); = (5, 16, 10). Показать, что векто-
Из координат векторов 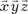 составляем определитель (2.35): составляем определитель (2.35):
Вторую строчку мы домножили на (-2) и сложили с первой, а затем полученный определитель разложили по элементам первого столбца. Определитель не равен нулю, поэтому векто- ры
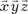 , т. е. , т. е. 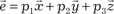 или или
Далее имеем:
Третье уравнение полученной системы умножаем на 3 и складываем со вторым. Тогда получаем:
И наконец вычислим
Таким образом, окончательно получим:
Задачи для самостоятельного решения 1.
1.1.
2.1. 2.2.
3.
3.1. 3.2. 3.3. 4.
4.1. 4.2.
5.1. 5.2.
6.1. 6.2. 6.3.
7. Дано: Найти угол между векторами 8. Даны два ортогональных вектора
Найти координату х 2. 9. В трехмерном пространстве заданы три точки М (1; 1; 1); N (2; 2; 2); P (4; 3; 5). Найти площадь треугольника MNP. 10. В трехмерном пространстве заданы четыре точки М (1; 1; 1); N (4; 4; 4); P (3; 5; 5); Q (2; 4; 7). Найти объем тетраэдра MNPQ. 11. Даны векторы 12. Проверить, что точки М (5; -1; -1); N (4; 2; 2); P (5; 3; 1); Q (8; 0; -5) лежат в одной плоскости. 13. Записать в матрично-векторном виде квадратичные формы: 13.1 f (х, х, х) = 7 x 2 − 3 x 2 − 0,5 x 2 − 5 х х + 17 х х + 22 х х. 1 2 3 1 2 3 1 2 1 3 2 3 13.2 f (х, х, х) = -32 x 2 − 0,5 x 2 + 11 x 2 + 92 х х − 66 х х − х х 1 2 3 1 2 3 1 2 1 3 2 3
Вопросы для самопроверки 1. Что называется матрицей? Типы матриц. 2. Правило и свойства сложения матриц. 3. Правило и основные свойства перемножения двух матриц. 4. Как найти матрицу, обратную заданной? Любая ли мат- рица имеет обратную? 5. Что называется определителем? 6. Что такое ранг матрицы? 7. Как определить, совместна ли заданная СЛАУ? 8. В каких случаях однородные СЛАУ имеют ненулевые решения? 9. В чем суть итерационных методов решения СЛАУ? 10. В чем состоит метод Гаусса решения СЛАУ? 11. В чем состоит метод Крамера решения СЛАУ? 12. Какие числа называются собственными значениями матрицы? 13. Что такое след матрицы? 14. Какое уравнение называется характеристическим уравнением матрицы? 15. Дать определение n-мерного векторного пространства. 16. Что называется нормой вектора? 17. Как найти угол между двумя векторами в n-мерном векторном пространстве? 18. Какое n -мерное пространство называется евклидовым? 19. Что называется квадратичной формой? 20. Приведите матрично-векторную запись квадратичной формы. 21. Дать определение векторного произведения. 22. Как находится веторное произведение, если заданы ко- ординаты составляющих его векторов? 23. Дать определение смешанного произведения векторов. Каков его геометрический смысл? 24. Как определить смешанное произведение, если заданы координаты составляющих его векторов?
Глава 3. ФУНКЦИИ И ПРЕДЕЛЫ
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 152; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |

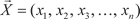 , числа x 1, х 2, х 3, …, х n есть координаты вектора, а n — его размерность.
, числа x 1, х 2, х 3, …, х n есть координаты вектора, а n — его размерность.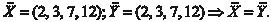
 .
.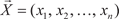

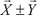 , каждая координата которого равна алгебраической сумме соответствующих координат векторов
, каждая координата которого равна алгебраической сумме соответствующих координат векторов 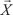 и
и  (2.21)
(2.21)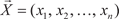 называется n -мерный вектор
называется n -мерный вектор  , каждая координата которого равна произведению числа k на соответс- твующую координату вектора
, каждая координата которого равна произведению числа k на соответс- твующую координату вектора 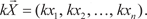 (2.22)
(2.22)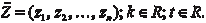
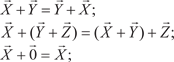 2)
2)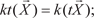
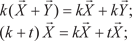 5)
5)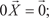


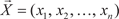 в пространстве Rn
в пространстве Rn
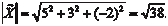
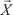
 ) называется число, получаемое по фор-
) называется число, получаемое по фор-
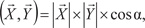
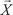 и
и 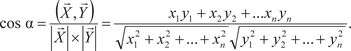

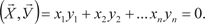
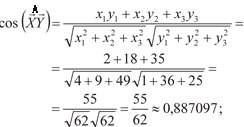
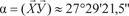
 — векторы в Rn, а k и t — действительные числа.
— векторы в Rn, а k и t — действительные числа. кулярных осей, которые пронумерованы в некотором порядке. Точка пересечения осей — это начало координат, а оси — это координатные оси, причем первую называют осью абсцисс (x), вторую — осью ординат (y), а третью — осью аппликат (z).
кулярных осей, которые пронумерованы в некотором порядке. Точка пересечения осей — это начало координат, а оси — это координатные оси, причем первую называют осью абсцисс (x), вторую — осью ординат (y), а третью — осью аппликат (z).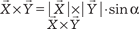
 Определение. Векторным произведением вектора на век- тор
Определение. Векторным произведением вектора на век- тор  и определяется следующими условиями:
и определяется следующими условиями: и б) вектор перпендикулярен к каждому из векторов
и б) вектор перпендикулярен к каждому из векторов

 к вектору
к вектору 
 и
и  коллинеарные векторы, то их векторное про- изведение равно нулю, т. е.
коллинеарные векторы, то их векторное про- изведение равно нулю, т. е. 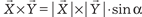 = 0.
= 0. и
и  равно нулю, то они коллинеарны.
равно нулю, то они коллинеарны. равен площади парал- лелограмма, построенного на этих векторах. Из элементарной геометрии известно, что площадь параллелограмма (S) рав- на произведению длин смежных сторон на синус угла между ними, т. е.
равен площади парал- лелограмма, построенного на этих векторах. Из элементарной геометрии известно, что площадь параллелограмма (S) рав- на произведению длин смежных сторон на синус угла между ними, т. е.  = S, поэтому имеем
= S, поэтому имеем  = S.
= S.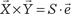 ,
,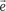


 Векторное произведение на — это вектор, обратный векторному произведению
Векторное произведение на — это вектор, обратный векторному произведению  на, т. е. .
на, т. е. .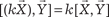
 , или
, или  .
.
 на вектор определяется формулой:
на вектор определяется формулой: . (2.28)
. (2.28)
 где
где  ,
,  ,
,  — орты координатных осей, т. е.
— орты координатных осей, т. е.  , а их расположение видно из рис. 2.4.
, а их расположение видно из рис. 2.4.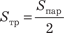


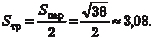
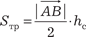
 — длина стороны АВ.
— длина стороны АВ.
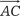
 или
или 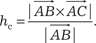
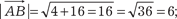
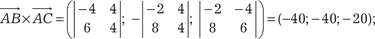
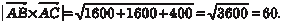

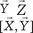 Определение. Смешанным произведением трех векторов
Определение. Смешанным произведением трех векторов  ,
, , скалярно умноженному на вектор
, скалярно умноженному на вектор  ,
,  ,
, 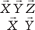 Геометрический смысл смешанного произведения виден из теоремы 2.5.
Геометрический смысл смешанного произведения виден из теоремы 2.5. ,
,  ,
, 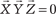 .
.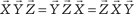 , т. е. смешанное произведение не ме- няется при циклической перестановке его сомножителей.
, т. е. смешанное произведение не ме- няется при циклической перестановке его сомножителей. ;
; 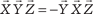 ;
; 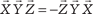 , т. е. смешан- ное произведение меняет свой знак при перестановке местами любых двух векторов-сомножителей.
, т. е. смешан- ное произведение меняет свой знак при перестановке местами любых двух векторов-сомножителей.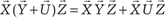
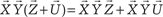
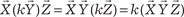 , где k ∈ R,
, где k ∈ R,




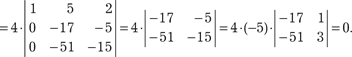
 ,
,  ,
,  компланарны.
компланарны.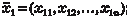
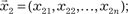
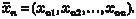
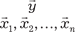
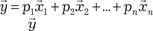 Любой вектор из пространства Rn единственным образом можно разложить по векторам базиса. Например, вектор мож- но разложить по линейно независимым векторам следующим образом: , где числа p 1, p 2, …, p n —координаты вектора в данном базисе.
Любой вектор из пространства Rn единственным образом можно разложить по векторам базиса. Например, вектор мож- но разложить по линейно независимым векторам следующим образом: , где числа p 1, p 2, …, p n —координаты вектора в данном базисе.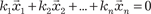

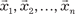 будет линейно зависимой и базиса не составляет.
будет линейно зависимой и базиса не составляет.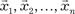 их координаты.
их координаты.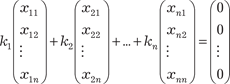
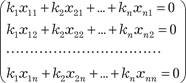

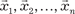 линейно независимы и со- ставляют базис пространства Rn.
линейно независимы и со- ставляют базис пространства Rn.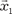 = (1, 0, 0, …, 0);
= (1, 0, 0, …, 0); 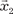 =
=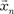 = (0, 0, 0, …, 1) базис пространства Rn?
= (0, 0, 0, …, 1) базис пространства Rn?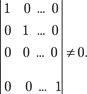
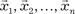 составляют базис пространства Rn.
составляют базис пространства Rn.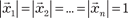
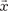
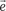
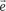

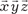 составляют базис пространства R 3.
составляют базис пространства R 3.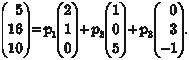
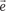

 .
.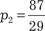
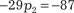
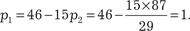
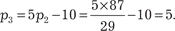
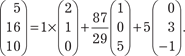
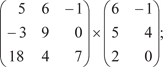
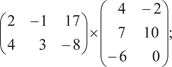
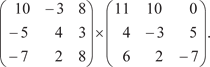

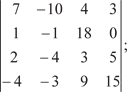
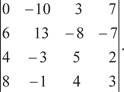
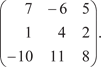
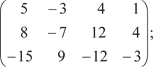
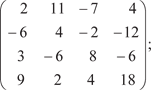
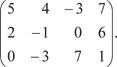







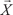 = (-4; -8; 8),
= (-4; -8; 8), 


