Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные уравнения 2-го порядкаСодержание книги
Поиск на нашем сайте
Общие понятия Дифференциальные уравнения второго порядка имеют следующий вид F (x, y, y ′, y ″) = 0, (6.33)
Если уравнение (6.33) можно разрешить относительно вто- рой производной, то получим одно или несколько уравнений вида y ″ = f (x, y, y ′). (6.34) Простейшим случаем дифференциального уравнения вто- рого порядка является дифференциальное уравнение вида y ″ = f (x), (6.35)
которое решают двукратным интегрированием, т. е.
В качестве примера найдем общее решение дифференци- ального уравнения Заметим, что дифференциальное уравнение вида (6.34) имеет бесконечное множество решений, которые задаются формулой y = ϕ(x, c 1, c 2), (6.36) содержащей две произвольные постоянные. Выражение вида (6.36) называется общим решением дифференциального урав- нения (6.34). Частное решение дифференциального уравнения (6.34) на- ходится при помощи задания начальных условий:

Найдем частные решения рассмотренного дифференци- ального уравнения y ″= x 2 при следующих начальных условиях
Тогда получаем следующую систему уравнений для на- хождения постоянных С 1 и С 2. Поэтому частное решение исходного дифференциального уравнения будет иметь вид:
Геометрический смысл начальных условий заключается в том, что помимо точки с координатами (х 0, у 0), через которую должна проходить интегральная кривая, задают еще угловой коэффициент касательной (y ′0) к этой кривой. Так как общее решение дифференциального уравнения второго порядка за- висит от двух произвольных постоянных, то через данную точ- ку проходит бесконечное множество интегральных кривых, но одна из них имеет заданный угловой коэффициент (y ′0). Будем считать, что правая часть дифференциального уравнения (6.34) f (x, y, y ′) является функцией трех независи- мых аргументов, так как при задании начальных условий ко- ординаты х 0, у 0 и угловой коэффициент касательной y ′0 ничем между собой не связаны. Тогда сформулируем теорему существования и единствен- ности решения дифференциального уравнения вида (6.34).
Теорема 6.2. Если функция f (x, y, y ′) непрерывна в окрес- тности значений х 0, у 0, y ′0, то дифференциальное уравнение вида (6.34) имеет решение y = y (x) такое, что y (x 0) = y 0 и y ′(x 0) = y ′0. Если кроме этого непрерывны и частные производные
Как и для дифференциального уравнения первого поряд- ка, задача отыскания частного решения по начальным услови- ям называется задачей Коши. Для дифференциальных уравнений второго порядка вы- деление частного решения можно проводить путем задания так называемых краевых условий. В этом случае задаются значе- ния функции у в двух различных точках
В качестве примера найдем частное решение дифферен- циального уравнения y ″= x 2 при следующих краевых условиях: Подставляя эти значения в общее решение исходного урав-
нения, получим систему уравнений для нахождения неизвест- ных постоянных С 1 и С 2. Таким образом, искомое частное решение имеет вид
В рассмотренном случае получилось одно частное реше- ние, удовлетворяющее заданным краевым условиям, но так бывает не всегда. Дифференциальное уравнение вида (6.34) мо- жет не иметь решения, удовлетворяющего заданным краевым условиям или иметь бесконечное множество таких решений. В этом состоит коренное отличие задания краевых условий от задания начальных условий.
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 221; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.82.70 (0.01 с.) |

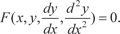
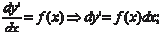

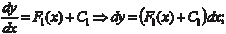

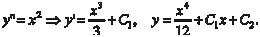
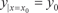
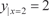 и
и 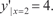
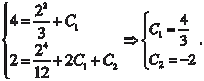
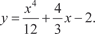
 и
и 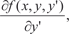 то это решение единственное [9, 44, 59].
то это решение единственное [9, 44, 59].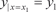 и
и 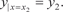
 и
и  .
.