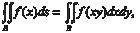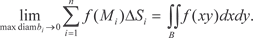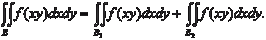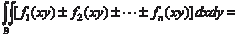Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приближенное вычисление определенных интеграловСодержание книги
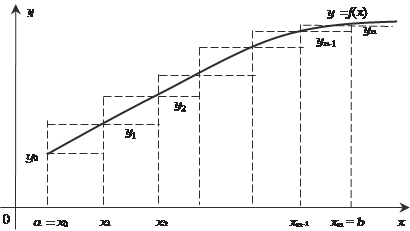
Поиск на нашем сайте В тех случаях, когда подынтегральная функция имеет сложный вид и неясно как ее преобразовать к табличной или же первообразная подынтегральной функции не выражается через элементарные функции, применяют приближенные ме- тоды вычисления определенных интегралов. Приведем несколько способов приближенного интегриро- вания, исходя из определения интеграла как предела суммы. а) Формула прямоугольников. Пусть на [ a,b ] задана непрерывная функция y = f (x). Надо вычислить
(рис. 5.23). Рис. 5.23 Значения функции y = f (x) в точках х 0, х 1, х 2,…, х n -1, х n обозначим через у 0, у 1, у 2,…, у n -1, у n. Теперь составим две суммы: S 1 = y 0 x + y 1 x + y 2 x +…+ y n-1 x, (5.17) где S 1 есть суммарная площадь прямоугольников, лежащих ниже y = f (x); S 2 = y 1 x + y 2 x +…+ y n x, (5.18) где S 2 есть суммарная площадь прямоугольников, лежащих выше y = f (x). Истинная площадь фигуры, ограниченная y = f (x), удов- летворяет условию S 1 < S ист < S 2. Поэтому можно записать приближенные равенства [4, 35]:
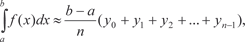 (5.19) (5.19)
(5.20)
Приближенные равенства (5.19) и (5.20) и есть формулы прямоугольников. Ошибка, которую мы совершаем при вычис- лении интегралов по формулам (5.19) и (5.20) будет тем меньше, чем больше n. Для того чтобы определить, сколько точек деле- ния надо взять, чтобы вычислить интеграл с заданной точнос- тью, надо использовать формулу оценки погрешности, которая получается при приближенном вычислении интеграла. Для ме- тода прямоугольников она имеет вид: где Приведем конкретный пример. Пример 5.45.
, взяв n = 10.
Заметим, что этот интеграл относится к числу неберущих- ся, т. е. он не выражается в элементарных функциях.
Используем для расчета формулу (5.19).
Теперь по формуле (5.19) имеем:
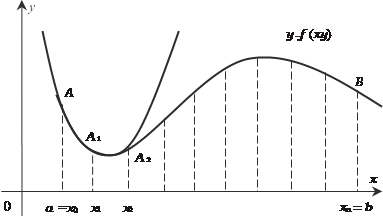
б) Формула трапеций. Более точное значение определенного интеграла, чем по (5.19) и (5.20), получим, заменив исходную функцию y = f (x) ломаной линией (рис. 5.24).
. Поэтому определенный интеграл приближенно будут равен:
(5.21)
Выражение (5.21) носит название формулы трапеций. A n -1 B
Формула оценки погрешности, получающейся при прибли- женном вычислении интеграла, в этом случае имеет вид [19]: где Приведем конкретный пример вычисления определенного интеграла по формуле (5.21). Пример 5.46.
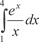 , приняв n = 10. Этот интеграл, как и интеграл пре- дыдущего примера, является неберущимся. В данном случае , приняв n = 10. Этот интеграл, как и интеграл пре- дыдущего примера, является неберущимся. В данном случае
.
Теперь по формуле (5.21) получаем в) Формула парабол (формула Симпсона). Пусть на отрезке [ a, b ] задана непрерывная функция y = f (x). Разделим [ a, b ] на четное число частей n = 2 m. Сущ- ность способа заключается в том, что отрезки прямых, ограни- чивающих элементарные трапеции сверху, заменяют дугами парабол, оси которых параллельны оси 0 у (рис. 5.25).
Рис. 5.25 Уравнения таких парабол имеет вид y = cx 2 + dx + p. Коэф- фициенты c, d, p можно однозначно найти по трем точкам, если абсциссы их различны. Дуги парабол проводят через каждую тройку точек. Криволинейную трапецию aABb заменяют сум- мой площадей криволинейных трапеций, ограниченных дуга- ми парабол. Площадь первой из таких параболических трапе- ций равна
Площадь n -й равна: Искомая формула Симпсона имеет вид [4, 35]:
Формула оценки погрешности, получающейся при прибли- женном вычислении интеграла, в этом случае имеет вид [19]: где
ность вычисления определенного интеграла. Метод прямоуголь- ников является наиболее простым и наименее точным способом. Выбор способа приближенного интегрирования зависит от по- дынтегральной функции и требуемой точности расчета. Приведем конкретный пример вычисления определенного интеграла по формуле (5.22). Пример 5.47.
По формуле (5.22) получим:
Понятие о двойном интеграле Понятие двойного интеграла является расширением поня- тия определенного интеграла на случай двух аргументов. На плоскости х 0 у рассмотрим замкнутую область В (об- ласть В называется замкнутой, если она ограничена линией и точки, которые лежат на границе, считаются принадлежащи- ми области В), ограниченную линией L. В этой области зада- дим непрерывную функцию z = f (x, y). Область В произволь- но разобьем на n частей (площадок): b 1, b 2, b 3, …, b n. Площади этих частей (площадок) обозначим S 1, S 2, …, S n. В каждой площадке b i
Рис. 5.26
(5.23)
Сумма (5.23) называется интегральной суммой для функ- ции z = f (x, y) в области В [44]. В случае, если z = f (x, y) 0 в области В каждое слагае- мое f (M i) S i есть объем цилиндра, площадь основания которого S i, а высота f (M i). А сумма V s представляет собой объем неко- торого ступенчатого тела (рис. 5.27).
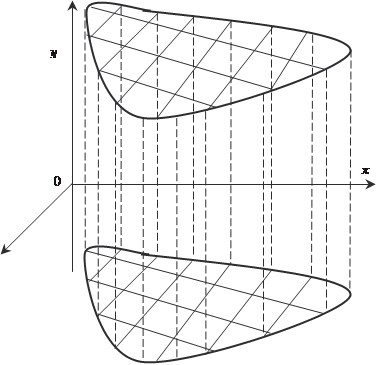
Рис. 5.27 Теперь рассмотрим произвольную последовательность ин- тегральных сумм, которые составлены с использованием фун- кции z = f (x, y) для области В:
при различных способах разбиении области В на площад- ки b i. Потребуем, чтобы максимальный диаметр площадок b i стремился к нулю (max diam b i → 0) при стремлении к бес- конечности количества этих площадок (n k →). Тогда будет справедлива следующая теорема, которую приводим без до- казательства. Теорема 5.4. Если функция z = f (x, y) непрерывна в за- мкнутой области В, то существует предел последовательнос-
ти (5.24) интегральных сумм (5.23), если максимальный диа- метр площадок b i → 0, а n →. Этот предел будет одинаков для любой последовательности вида (5.24), т. е. он не зависит ни от способа разделения области В на площадки b i, ни от выбора в этих площадках точек M i. Этот предел называется двойным ин- тегралом от функции z = f (x, y) по области В и обозначается т. е.
Если z = f (x, y) 0, двойной интеграл от этой функции по области В равен объему тела, ограниченного поверхностью z = f (x, y), плоскостью х 0 у и цилиндрической поверхностью, образующие которой параллельны оси 0 z, а направляющей служит линия L.
Свойства двойного интеграла 1.
Если область В разбить на две части В 1 и В 2, то Аналогично при разбиении области В на число частей боль- ше двух. 2.
Двойной интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме двойных интегра- лов от этих функций, т. е.
3. Постоянный множитель можно выносить за знак двойно- го интеграла, т. е.
где с — постоянная величина.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 189; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.007 с.) |

 . Отрезок [ a, b ] разделим точками а = х 0, х 1, х 2,…, х n -1, х n = b на n одинаковых частей длины х, где
. Отрезок [ a, b ] разделим точками а = х 0, х 1, х 2,…, х n -1, х n = b на n одинаковых частей длины х, где 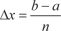
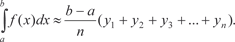
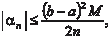
 [19].
[19].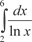
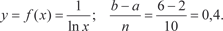
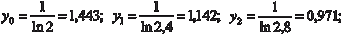
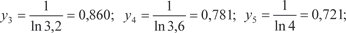
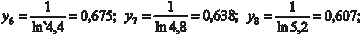
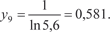
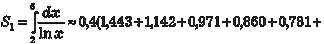


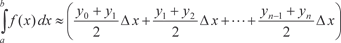
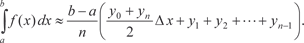
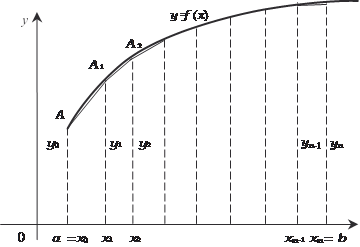
 Рис. 5.24
Рис. 5.24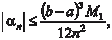
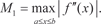
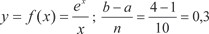
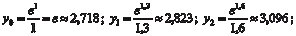
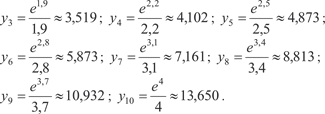
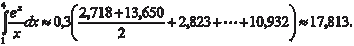
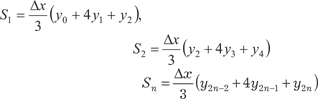 площадь второй равна: .
площадь второй равна: .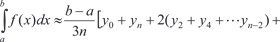
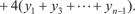 (5.22)
(5.22)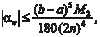
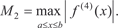
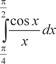
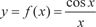
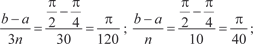
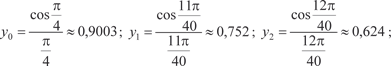
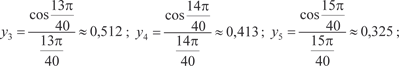
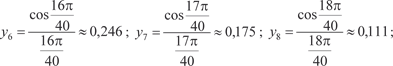
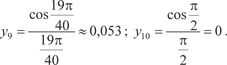
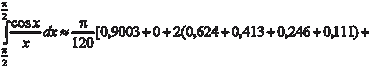
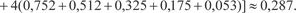
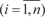 возьмем произвольную точку M i (эта точка может лежать и на границе площадки). Таким образом, будем иметь n точек: М 1, М 2, …, М n (рис. 5.26).
возьмем произвольную точку M i (эта точка может лежать и на границе площадки). Таким образом, будем иметь n точек: М 1, М 2, …, М n (рис. 5.26).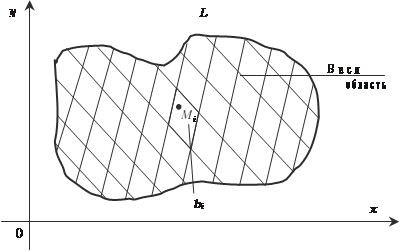
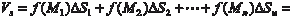
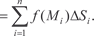
 z
z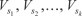 (5.24)
(5.24)