Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графический метод решения задач линейного программирования
Графический метод решения задач ЛП основан на их гео- метрической интерпретации и применяется для задач, имею- щих две переменные. В случае трех переменных графическое решение задачи ЛП становится менее наглядным, а при боль- шем числе переменных вообще невозможным. Графическим методом решение получают в результате последовательно выполняемых шагов, содержание которых составляют: 1) построение области допустимых решений (ОДР); 2) поиск точки ОДР, соответствующей оптимальному ре- шению; 3) определение координат этой точки. 1. Построение области допустимых решений. Область допустимых решений представляет собой часть плоскости (в многомерном случае — часть гиперпространства), все точки которой удовлетворяют всем ограничениям, имеющимся в дан- ной задаче ЛП. Условие неотрицательности переменных x1 ≥ 0, x2 ≥ 0 ограничивает область их допустимых значений первым квадрантом. Другие границы ОДР на плоскости x10 x2 изобра- жаются прямыми линиями, построенными на основе ограниче- ний при замене в них знаков неравенства знаками равенства. Каждая линия определяет на плоскости две области: в одной из них все точки удовлетворяют заданным ограничениям, в другой — нет. Ту область, в которой выполняются ограниче- ния в виде неравенств, указывают стрелками, направленными в сторону допустимых значений переменных. Кроме того, для удобства восприятия возле каждой линии проставляют номер соответствующего ограничения. В каждой точке ОДР, принадлежащей внутренней области или границе образовавшегося выпуклого многоугольника, все ограничения выполняются. Поэтому решения, соответствующие этим точкам, являются допустимыми. С содержательной точки зрения каждая точка ОДР представляет собой конкретную стра- тегию проведения операции u = (x1, x2), а множество всех точек ОДР — множество всех возможных стратегий U = {u}. 2. Поиск оптимальной точки ОДР. Построенная ОДР представляет собой выпуклый многоугольник. В теории линей- ного программирования доказывается, что своего оптимального значения ЦФ достигает в угловой (или экстремальной) точке выпуклого многоугольника решений. Если ЦФ задавать неко- торые фиксированные возрастающие значения W(x) = c1x1 + + c2x2 = const, то полученные уравнения на плоскости опре-
Для практического осуществления поиска оптимальной точки ОДР необходимо: 1) определить вектор градиента ЦФ ∇ W(x) = (∂W(x)/∂x1; ∂W(x)/∂x)т = (c, c)т. Длина вектора градиента не связана со зна- 2 1 2 чением ЦФ, поэтому достаточно указать лишь его направление; 2) построить прямую, перпендикулярную вектору гради- ента; 3) перемещая эту прямую параллельно самой себе в на- правлении вектора градиента дойти до угловой точки ОДР, где ЦФ достигает максимального допустимого значения. 3. Определение значений управляемых переменных. Ре- шение задачи ЛП составляют координаты (x1, x2) угловой точки ОДР, через которую проходит линия, соответствующая урав- нению ЦФ. Числовые значения этих переменных получают из решения системы линейных уравнений, которым на графике соответствуют пересекающиеся линии. Пример 9.1. Определить max W(x) = x1 + 4x2 при ограничениях: x1 + x2 ≤ 4; − x1 + x2 ≤ 2; x1, x2 ≥ 0. Графическое решение задачи представлено на рис. 9.1.
Рис. 9.1. Графическое решение задачи ЛП Решение задачи составляют: 1) значение целевой функции W(x) = 13; 2) координаты экстремальной точки u = {x1 = 1, x2 = 3}. Нахождение решения задачи ЛП на основе ее геометри- ческой интерпретации включает следующие этапы: 1. Строят прямые, уравнения, которых получаются в ре- зультате замены в ограничениях знаков неравенств на знаки точных равенств. 2. Находят полуплоскости, определяемые каждым из ог- раничений задачи. 3. Находят многоугольник решений. 4. Строят вектор С = (с1; с2). 5. Строят прямую с1x1 + c2x2 = h, проходящую через мно- гоугольник решений. 6. Передвигают прямую с1x1 + c2x2 = h в направлении век- тора С, в результате чего либо находят точку (точки), в которой целевая функция принимает максимальное значение, либо устанавливают неограниченность свер- ху функции на множестве планов.
7. Определяют координаты точки максимума функции и вычисляют значение целевой функции в этой точке. Пример 9.2. Для производства двух видов изделий (А и В) предприятие использует три вида сырья. Нормы расхода сырья каждого вида на изготовление единицы продукции данного вида приведены в табл. 9.1. В ней же указана прибыль от реализации одного изде- лия каждого вида и общее количество сырья данного вида, кото- рое может быть использовано предприятием. Таблица 9.1 Вид сырья | Нормы расхода сырья (кг) на одно изделие | Общее коли- чество сырья (кг) | ||||||||
| А | В | ||||||||||
| I | 12 | 4 | 300 | ||||||||
| II | 4 | 4 | 120 | ||||||||
| III | 3 | 12 | 252 | ||||||||
| Прибыль от реализации одного изделия | 30 | 40 | |||||||||
Учитывая, что изделия А и В могут производиться в лю- бых соотношениях (сбыт обеспечен),требуется составить такой план, при котором прибыль предприятия от реализации всех изделий является максимальной.
Решение. Предположим, что предприятие изготовит x1 изделий вида А и x2 изделий вида В. Поскольку производство продукции ограничено имеющимися в распоряжении предпри- ятия сырьем каждого вида и количество изготовляемых изде- лий не может быть отрицательным, должны выполняться не- равенства:
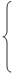 12x1 + 4x2 ≤ 300,
12x1 + 4x2 ≤ 300,
4x1 + 4x2 ≤ 120,
3x1 + 12x2 ≤ 252,
x1, x2 ≥ 0
Общая прибыль от реализации x1 изделий вида А и x2 из- делий вида В составит W(x) = 30x1 + 40x2.
Таким образом, мы переходим к следующей математичес-
кой задаче: среди всех неотрицательных решений данной сис- темы линейных неравенств следует найти такое, при котором функция W(x) принимает максимальное значение.
Найдем решение сформулированной задачи, используя ее геометрическую интерпретацию. Сначала определим мно- гоугольник решений. Для этого в неравенствах системы огра- ничений и условиях неотрицательности переменных знаки неравенств заменим знаками точных равенств и найдем соот- ветствующие прямые:
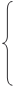 12x1 + 4x2 = 300, (I)
12x1 + 4x2 = 300, (I)
4x1 + 4x2 = 120, (II)
3x1 + 12x2 = 252, (III) x1 = 0, (IV)
x2 = 0. (V)
Эти прямые изображены на рис. 9.2.
Каждая из построенных прямых делит плоскость на две полуплоскости. Координаты точек одной полуплоскости удов-
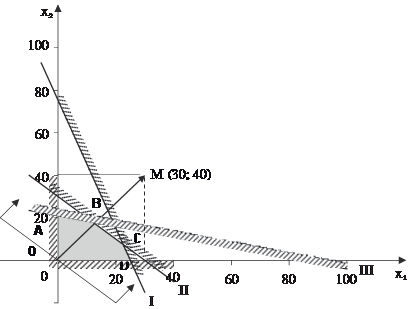
Рис. 9.2
летворяют исходному неравенству, а другой нет. Чтобы опре- делить искомую полуплоскость, нужно взять какую-нибудь точку, принадлежащую одной из полуплоскостей, и прове- рить, удовлетворяют ли ее координаты данному неравенс- тву. Если координаты взятой точки удовлетворяют данному неравенству, то искомой является та полуплоскость, которой принадлежит эта точка, в противном случае — другая полу- плоскость.
Найдем, например, полуплоскость, определяемую нера- венством 12x1 + 4x2 ≤ 300. Для этого, построив прямую 12x1 +
+ 4x2 = 300 (I), возьмем какую-нибудь точку, принадлежащую
одной из двух плоскостей, например точку О(0;0). Координаты этой точки удовлетворяют неравенству 12·0 + 4·0 < 300; значит, полуплоскость, которой принадлежит точка О(0;0), определя- ется неравенством 12x1 + 4x2 ≤ 300. Это и показано стрелками на рис. 9.2.
Пересечение полученных полуплоскостей и определяет многоугольник решений данной задачи.
Как видно из рис. 9.2, многоугольником решений являет- ся пятиугольник OABCD. Координаты любой точки, принадле- жащей этому пятиугольнику, удовлетворяют данной системе неравенств и условию неотрицательности переменных. Поэто- му сформулированная задача будет решена, если мы сможем найти точку, принадлежащую пятиугольнику OABCD, в кото- рой функция W(x) принимает максимальное значение. Чтобы найти указанную точку, построим вектор С = (30; 40) и прямую 30x1 + 40x2 = h, где h — некоторая постоянная такая, что пря- мая 30x1 + 40x2 = h имеет общие точки с многоугольником ре- шений. Положим, например, h = 480 и построим прямую 30x1 +
|
|
+ 40x2 = 480.
Если теперь взять какую-нибудь точку, принадлежащую построенной прямой и многоугольнику решений, то ее коорди- наты определяют такой план производства изделий А и В, при котором прибыль от их реализации равна 480 руб. Далее, пола- гая h равным некоторому числу, большему чем 480, мы будем получать различные параллельные прямые. Если они имеют общие точки с многоугольником решений, то эти точки опреде- ляют планы производства изделий А и В, при которых прибыль от их реализации превзойдет 480 руб.
Перемещая построенную прямую 30x1 + 40x2 = 480 в на- правлении вектора С, видим, что последней общей точкой ее с многоугольником решений задачи служит точка В. Координа- ты этой точки и определяют план выпуска изделий А и В, при котором прибыль от их реализации является максимальной.
Найдем координаты точки В как точки пересечения пря- мых II и III. Следовательно, ее координаты удовлетворяют уравнениям этих прямых:
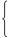 4x1 + 4x2 = 120,
4x1 + 4x2 = 120,
3x1 + 12x2 = 252.
Решив эту систему уравнений, получим x1 = 12, x2 = 18. Следовательно, если предприятие изготовит 12 изделий вида А
и 18 изделий вида В, то оно получит максимальную прибыль, равную W(x)max = 30·12 + 40·18 = 1080 руб.
Содержательная интерпретация полученных результатов
приводит к следующим выводам:
1) изделий первого вида должно быть произведено 12 еди- ниц; изделий второго вида — 18 единиц;
2) на производство изделий задействовано полностью сы- рье 3-го и 2-го вида; при этом будет сэкономлено 216 единиц сырья 1-го вида;
выручка, соответствующая оптимальной организации про- изводства, составит 1080 у.д.е.