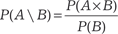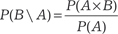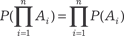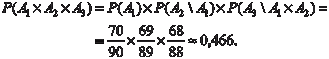Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приближенное решение дифференциальных уравненийСодержание книги
Поиск на нашем сайте В том случае, если решение дифференциального уравне- ния не выражается через элементарные функции или метод его решения слишком сложен, для его приближенного решения можно использовать ряд Тейлора. Предположим, что надо решить дифференциальное урав- нение
которое удовлетворяет начальным условиям:
Для нахождения частного решения используем метод пос- ледовательного дифференцирования. Предположим, что решения дифференциального уравне- ния в окрестности точки x 0, в которой заданы начальные усло- вия, можно разложить в ряд Тейлора.
Первые два коэффициента в ряде (7.12) можно определить по начальным условиям (7.11). Затем подставляем в исходное дифференциальное уравнение (7.10) значение x = x 0, y = y 0, y = y 0 и определяем третий коэффициент: y (x 0) = f (x 0, y 0, y). Значение последующих коэффициентов y (x), y (4) (x), …, 0 0 0
Он и является частным решением исходного дифференци- ального уравнения (7.10) для тех значений x, для которых он сходится. Частичная сумма этого ряда есть приближенное ре- шение уравнения (7.10) при начальных условиях (7.11). Данный метод можно применять решения дифференци- альных уравнений любого порядка. Пример 7.15. Используя метод последовательного дифференцирования найти частное решение дифференциального уравнения y = x
 . .
Будем искать решение данного дифференциального урав- нения в виде ряда Тейлора:
Используя заданные начальные условия, определяем:
 . Затем находим. Для этого подставляем в исходное дифференциальное уравнение x = 1 и и полу- чаем: . Затем находим. Для этого подставляем в исходное дифференциальное уравнение x = 1 и и полу- чаем: 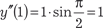 . Для нахождения последующих коэффи- циентов дифференцируем по x заданное дифференциальное уравнение и получаем: . Для нахождения последующих коэффи- циентов дифференцируем по x заданное дифференциальное уравнение и получаем:
Далее имеем:
Подставляем значения найденных производных в ряд и получаем искомое приближенное частное решение заданного дифференциального уравнения.
Понятие о рядах Фурье Сначала напомним, что функция f (х), которая определена при всех значениях х, называется периодической, если есть такое число Т 0, что при любом значении х выполняется ра- венство f (х + Т) = f (х). В этом случае Т называется периодом функции. Приведем некоторые свойства периодических функций: 1. Сумма, разность, произведение, частное периодических функций с периодом Т есть периодические функции периода Т. 2. Если функция f (х) имеет период Т, то функция f (bх) имеет период Т / b. 3.
. Дадим также понятия о гармонических колебаниях. Простое гармоническое колебание описывается функцией у = А ·sin (t + 0), где у — отклонение колеблющейся точки от положения равно- весия; А — амплитуда колебания; = 2π/ Т — круговая частота; 0 — начальная фаза. Функция А · sin(t + 0) и ее график называется простой гармоникой. Ее можно представить в виде А · (sin t ·cos 0 + + cos t · sin 0). То есть простое гармоническое колебание описывается пе- риодическими функциями sin t и cos t. Колебания, которые получаются в результате сложения не- скольких или бесконечно многих простых гармонических коле- баний, тоже будут описываться функциями вида sin t и cos t. С помощью так называемого тригонометрического ряда практически любую периодическую функцию можно разло- жить на простые гармоники. Тригонометрическим рядом называется функциональный ряд вида: а 0/2 + а 1cos х + b 1sin x + а 2cos2 x + b 2sin2 x + … + + а n cos nx + b n sin nx +… где a 0, a 1, b 1, a 2, b 2, …, a n, b n — коэффициенты тригонометричес- кого ряда. Если ряд (7.13) сходится, то его сумма есть периодическая функция с периодом 2π, так как такой период имеют функции sin nx и cos nx. Поэтому f (х) = f (х + 2π). Предположим, что функция f (х) с периодом 2π такова, что она представляется тригонометрическим рядом, сходящимся к данной функции в интервале (-π, π), т. е. является суммой этого ряда и записывается следующим образом:
; (7.15)
то они называются коэффициентами Фурье, а тригонометри- ческий ряд (7.13) с такими коэффициентами называется рядом Фурье функции f (х). Теперь сформулируем теорему, которая дает достаточные условия представимости функции f (х) рядом Фурье. Теорема 7.4 (теорема Дирихле). Пусть функция f (х) с периодом 2π на отрезке [-π, π] удов- летворяет следующим условиям: 1) f (х) кусочно-монотонна, т. е. монотонна на всем отрезке, или этот отрезок можно разбить на конечное число интервалов таким образом, что на каждом из них функция будет монотонна; 2) f (х) кусочно-непрерывна, т. е. непрерывна или имеет ко- нечное число точек разрыва первого рода. В этом случае соответствующий функции f (х) ряд Фурье сходится на данном отрезке и при этом: а) в точках непрерывности функции сумма ряда S (x) сов- падает с самой функцией, т. е. S (x) = f (x); б) в каждой точке разрыва (х 0) функции f (х) сумма ряда равна
т. е. она равна среднему арифметическому от правого и левого пределов в этой точке; в) на концах отрезка в точках х =-π и х = π сумма ряда равна
Теореме Дирихле удовлетворят большинство функций, встречающихся в математике. Есть функции, которые не удов- летворяют условиям Дирихле, но разлагающиеся в ряд Фурье, так как теорема 7.4 дает только достаточное условие разложи- мости. Приведем конкретный пример разложения функции в ряд Фурье. Пример 7.16. Пусть периодическая функция f (х) с периодом 2π опреде- лена следующим образом: f (х) = х, х ∈ (-π; π].
Данная функция является кусочно-монотонной и ограни- ченной, т. е. она может быть разложена в ряд Фурье. Применя- ем формулы (7.15)−(7.17) и находим:
Поэтому получаем ряд Данное равенство имеет место во всех точках, за исключе- нием точек разрыва. В каждой точке разрыва сумма ряда есть среднее арифметическое от ее пределов слева и справа, т. е. равна нулю. Задачи для самостоятельного решения 1. С помощью признаков сравнения исследовать сходи- мость рядов: 1.1. 1.3. 2. Исследовать сходимость рядов с помощью признака Да- ламбера: 2.1. 2.2. 3. Исследовать сходимость рядов с помощью признака Коши: 3.1. 3.2. 4.
4.1. 4.2.
дов: 5. Исследовать абсолютную или условную сходимость ря-
5.3. 6. Найти области сходимости степенных рядов:
7. Разложить в ряд Фурье периодическую функцию с пе- риодом 2π. 7.1. f (х) = | х |, где х ∈ (-π, π).
где x ∈ (0; π). 8. Вычислить определенный интеграл с точнос- тью до 0,01. 9.
Вопросы для самопроверки 1. Что называется числовым рядом? 2. Что такое сумма ряда? Дать определение сходящегося и расходящегося рядов. 3. В чем состоит необходимый признак сходимости ряда? 4. В чем суть признаков Даламбера и Коши? 5. В чем суть интегрального признака Коши? 6. Какой ряд называется знакочередующимся? 7. В чем сущность признака Лейбница? 8. Что называется абсолютной и условной сходимостью ряда? 9. Какой ряд называется функциональным? 10. Что называется областью сходимости функционально- го ряда? 11. Какой ряд называется степенным? 12. Каковы основные свойства степенных рядов? 13. Какой ряд называется тригонометрическим? 14. Сформулируйте достаточный признак разложения функции в ряд Фурье. 15. В каких случаях используют ряды для вычисления оп- ределенных интегралов? 16. В чем состоит способ последовательного дифференци- рования?
Глава 8. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ВЕРОЯТНОСТЕЙ 8.1. Общие понятия и определения Теория вероятностей — раздел математики, который занимается изучением закономерностей в случайных явле- ниях. Случайное явление — это явление, которое при многократ- ном проведении одного и того же опыта (эксперимента) каждый раз протекает несколько по-иному. Теория вероятностей рас- сматривает не сами явления, а их математические модели. Ма- тематическая модель описывает изучаемое явление при помо- щи определенных символов и операций над ними. Под опытом (экспериментом) будем понимать некоторую воспроизводимую совокупность условий, в которых наблю- дается изучаемое явление. Если результат опыта может ва- рьироваться при его повторении, то говорят об опыте со слу- чайным исходом. Основные условия, при которых протекает опыт, должны сохраняться. Опыт не обязательно должен быть поставлен людьми, человек может выступать и в качестве на- блюдателя. Примерами случайных явлений являются: курс национальной валюты, выпадение грани с цифрой шесть при бросании игральной кости, выигрыш на рулетке в казино, ре- зультат измерения горизонтального угла с помощью теодоли- та, длительность работы стиральной машины и т. д. Классификация событий Если событие всегда происходит в результате опыта со случайным исходом, то оно называется достоверным. Такие события мы будем обозначать буквой U. Если в урне лежат только красные шары, то появление красного шара из урны есть достоверное событие. Надо иметь в виду, что в реальной действительности мы имеем дело с почти достоверными собы- тиями. Если событие никогда не происходит в результате опыта со случайным исходом, то оно называется невозможным и обозна- чается ∅. Если в урне лежат только белые шары, то появление красного шара из урны есть невозможное событие. В реальной жизни мы имеем дело с почти невозможными событиями. Случайным событием называется событие, которое в ре- зультате опыта со случайным исходом может произойти, а мо- жет и не произойти. Случайные события мы будем обозначать заглавными буквами латинского алфавита: А, В, С,… Например, выпадение решки при бросании монеты — случайное событие. Событием, противоположным событию А, является собы- тие Например, производится стрельба по мишени. Собы- тие А — попадание в мишень, а событие Непосредственный исход опыта называется элементар- ным событием и обозначается ω. Множество всех элементарных событий данного конкрет- ного опыта называется пространством элементарных событий этого опыта и обозначается Ω. Например, в опыте бросания игральной кости шесть эле- ментарных исходов ω1, ω2,…, ω6, т. е. Ω = {ω1, ω2, ω3, ω4, ω5, ω6}. Событие удобно иллюстрировать с помощью кругов Эйле- ра. Достоверное событие U мы будем изображать прямоуголь- ником, случайное событие А — кругом внутри прямоугольника, а противоположное к нему событие
Рис. 8.1 Алгебра событий Введем понятия суммы и произведения событий.
.
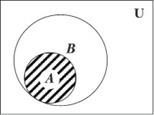
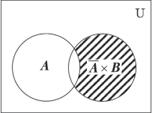
Определение. Произведением (пе- ресечением) событий А1, А2,... Аn назы- вается событие, которое происходит только в том случае, когда все указан- ные события появляются одновремен- но, т. е. происходит и событие А1, и А2... и Аn. Обозначается произведение со- бытий следующим образом: Рис. 8.2
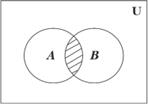
Рис. 8.3 На рис. 8.3. показано изображение произведения двух событий А × В с по- мощью кругов Эйлера. Определение. События А1, А2,... Аn называются несовместными, если их произведение есть невозможное собы- тие, т. е. А1 · А2 ·... · Аn = ∅. Заметим, что если события попарно несовместны, то они несовместны в совокупности. Не- совместными являются все элементарные события некоторого опыта со случайным исходом, например А ×
Определение. Полной группой со- бытий называется множество попар- но несовместных событий, одно из ко- торых обязательно произойдет в ре- зультате опыта со случайным исхо- дом, т. е. сумма которых есть достовер- Рис. 8.4 ное событие.
Все элементарные события ωi пространства элементарных событий Ω составляют полную группу событий. Например, пол- ную группу событий составляют события А и
Рис. 8.5 Приведем некоторые правила алгебры событий:
 × В (рис. 8.6). × В (рис. 8.6).
Рис. 8.6 Вероятность события Вероятность события — это мера его объективной возмож- ности. Но данное определение вероятности не является мате- матическим, так как не дает возможности оценить вероятность количественно. Существует несколько математических опре- делений вероятности. Самыми старыми из этих определений являются статистическое и классическое определения. Статистическое определение вероятности. Предположим, что мы можем проводить некоторый опыт со случайным исхо- дом (например, бросание монеты на некоторую поверхность) неоднократно, примерно в одних и тех же условиях. В резуль- тате этого опыта может появиться событие А = {выпал герб}. Определение. Относительной частотой (или, как говорят в статистике, частостью) события А (f (А)) называется отноше- ние числа опытов µ (его называют в статистике частотой собы- тия А), в которых появилось событие А, к общему числу прове- денных опытов (n), т. е.
Практика показывает, что для широкого круга случайных явлений при неограниченном увеличении числа опытов, т. е. при n → ∞, относительная частота события А стабилизирует- ся и по вероятности приближается к некоторому неслучайному числу. Например, при бросании монеты относительная частота появления орла при неограниченном увеличении числа опытов стремится к числу 0,5. Приведем свойства относительной ча- стоты события А. 1) f (U) = 1, так как µ = 1. 2) f (∅) = 0, так как µ = 0. 3) 0 ≤ f (А) ≤ 1, т. е. относительная частота случайного собы- тия заключена между нулем и единицей и в частном случае мо- жет быть нулем или единицей. 4) Если события А1, А2,... Аn несовместны, то выполняется равенство f (А1 + А2 +…+ Аn) = f (А1) + f (А2) +…+ f (Аn). Статистическое определение вероятности. Вероятностью события А (Р (А)) называется число, около которого колеблется относительная частота события А (f (А)) при неограниченном увеличении числа опытов (n → ∞). То есть можно записать
или
где ε > 0 — малое положительное число. Устойчивость относительных частот при большом коли- честве испытаний является следствием закона больших чисел. Характер приближения относительной частоты к вероят- ности при n → ∞ отличается “от стремления к пределу” в мате- матическом анализе. Нет ничего невозможного в том, что относительная частота события при n → ∞ сильно отклонится от ее вероятности, но та- кое отношение настолько маловероятно, что его можно не при- нимать в расчет. Заметим, что все свойства относительных частот верны и для вероятностей. Классическое определение вероятности. Оно было впер- вые четко сформулировано в работе швейцарского математи- ка Якоба Бернулли, опубликованной в 1713 г. Введем понятие равновозможного события. События называются равновозмож- ными, если по условиям обыта ни одно из них не является пред- почтительным по отношению к другим с точки зрения возмож- ности их появления. В этом случае опыт будет обладать симметрией исходов по отношению к этим событиям. Классическое определение вероятности можно использо- вать только в том случае, если опыт будет классическим. Опыт называется классическим, если он приводит к множеству со- бытий, которые удовлетворяют условиям: 1) они попарно несовместны; 2) равновозможны; 3) образуют полную группу событий. Такие события называются случаями и обозначаются ω. Заметим, что они могут быть элементарными событиями.
. (8.4)
Формула (8.4) дает возможность непосредственно вычис- лять вероятности, но недостатком ее является то, что в реаль- ной действительности классические опыты встречаются редко в искусственно созданных ситуациях. Примером классического опыта является игра в кости, которые перед каждым броском тщательно перемешиваются, чтобы соблюдалась равновозмож- ность наблюдаемых событий. Если мы бросаем одну игральную кость, то вероятность появления каждой ее грани равна 1/6. Классический опыт может быть организован по так назы- ваемой урновой схеме. Под урной понимают некоторый ящик, в котором находятся одинаковые по весу и размерам шары раз- личных цветов. После перемешивания шары вынимаются из урны случайным образом. Поэтому вероятность вытащить ка- кой-либо шар из n шаров будет равна 1/ n. Для подсчета числа возможных исходов классического опыта часто используют формулы комбинаторики, в частности формулы числа сочетаний из n элементов по m: − без повторений:
где n! — читается n -факториал и вычисляется по формуле n! = 1 × 2 × 3… × n; − с повторениями:
Пример 8.1. Предположим, что в урне находятся 9 шаров: четыре крас- ных шара и пять синих шаров. Из нее вынимаются два шара. Надо найти вероятность того, что оба они будут красными.
Введем событие А = {оба шара красные} и используем фор- мулу (8.4): Здесь — количество исходов, благоприятствующих событию А; — общее количество исходов.
Аксиоматическое построение теории вероятностей было осуществлено в 30-х гг. XX в. А. Н. Колмогоровым. Приведем его упрощенное определение. Вероятностью называется функция событий, которая по- рождена некоторым опытом и имеет следующие свойства: 1) вероятность достоверного события равна единице Р (U) = 1; 2) вероятность невозможного события равна нулю Р (∅) = 0; 3) вероятность случайного события лежит между нулем и единицей, в частности принимая значение ноль и единица 0 ≤ Р (А) ≤ 1; 4) если события А1, А2,... Аn попарно несовместны, то веро- ятность их суммы равна сумме их вероятностей
5) если счетное бесконечное число событий А1, А2,... Аn, … попарно несовместно, то вероятность их суммы равна суме их вероятностей, т. е.
Аксиома 5 вводится отдельно, так как она не выводится из четвертой. Кроме приведенного существуют и другие аксиоматичес- кие определения вероятности. Аксиоматическое определение, в отличие от статистичес- кого и классического, не позволяет непосредственно вычислять значение вероятности, но из него вытекает ряд следствий. На- пример, можно получить формулу (8.4), установить, что сумма вероятностей полной группы событий равна единице, т. е.
В частности получаем Р (А) + Р ( т. е. сумма вероятностей противоположных событий равна 1. Субъективное определение вероятности. В тех случаях, когда проводимый опыт не является классическим и отсутству- ют данные статистических наблюдений или их недостаточное количество для оценки вероятности, прибегают к экспертному оцениванию вероятности на основе мнения экспертов. Определение. Субъективным определением вероятности называются вероятности, удовлетворяющие аксиомам 1−5 ак- сиоматического определения, которые приписываются собы- тиям на основе мнения экспертов. Как правило, в оценке вероятности события участвуют несколько экспертов, и их мнения усредняют, учитывая опыт каждого из них. Оценка экспертов важна в тех случаях, если планируемый исход связан с большими материальными за- тратами.
Алгебра вероятностей Рассмотрим правила, которые позволяют по вероятностям одних событий находить вероятности других событий. Сначала введем понятие условной вероятности. Предполо- жим, что А и В — события, являющиеся результатом некоторо- го опыта, причем наступление события А зависит от появления события В. Понятие условной вероятности вводится для харак- теристики зависимости одних событий от других. Определение. Условной вероятностью события А при усло- вии, что произошло событие В, называется отношение вероят- ности произведения событий А и В к вероятности события В, если последняя отлична от нуля. Обозначается условная веро- ятность события А следующим образом: Р(А\В). И согласно оп- ределению, она равна
Р (В) ≠ 0. Аналогично условная вероятность события В при условии, что произошло событие А обозначается следующим образом: Р(В\А) и находится по формуле
Р (А) ≠ 0. Из формул (8.7.) и (8.8) следует правило умножения веро- ятностей для двух любых событий: Р (А × В) = Р (А) × Р (В\А) = Р (В) × Р (А\В), (8.9) т. е. вероятность произведения двух событий равна произведе- нию вероятности одного из них на условную вероятность дру- гого при условии, что первое событие произошло. Используя формулу (8.9), получим правило умножения ве- роятностей для трех событий А1, А2, А3: Р (А 1 × А 2 × А 3) = Р ((А 1 × А 2) × А 3) = = Р (А 1 × А 2) × Р (А 3 \А 1 × А 2) = (8.10) = Р (А 1) × Р (А 2 \А 1) × Р (А 3 \А 1 × А 2) В формуле (8.10) Р (А 3 \А 1 × А 2) означает условную вероят- ность события А3, если произошли события А1и А2. Используя принцип математической индукции, можно обобщить формулу (8.10) на любое конечное количество со- бытий. В результате получаем Р (А 1 × А 2 × А 3… × А n) = Р (А 1) × Р (А 2 \А 1) × × Р (А 3 \А 1 × А 2) × … × Р (А n \А 1 × А 2 × А 3 ×… × А n -1). (8.11) Правило умножения вероятностей значительно упроща- ется, если события, образующие произведение, независимы. Событие В называется независимым от события А, если его условная вероятность равна безусловной, т. е. Р(В\А) = Р (В). Аналогично, событие А называется независимым от собы- тия В, если его условная вероятность равна безусловной, т. е. Р (А\В) = Р (А). Лемма. Если событие В не зависит от события А, то и со- бытие А не зависти от события В. Если события А и В независимы, то правило умножения вероятностей (8.9) примет вид Р (А × В) = Р (А) × Р (В), (8.12) т. е. вероятность произведения двух независимых событий рав- на произведению их вероятностей. Определение. События А1, А2, А3... Аn называются независи- мыми в совокупности, если каждое из них не зависит от произве- дения любого числа остальных и от каждого в отдельности. Правило умножения вероятностей (8.11) в этом случае примет вид: Р (А 1 × А 2 × А3 × … × А n) = Р (А 1) × Р (А 2) × Р (А 3) × … × Р (А n), или более кратко
т. е. вероятность произведения конечного числа независимых событий равна произведению вероятностей этих событий. Пример 8.2. Предположим, что студентка основательно проштудиро- вала 70 из 90 вопросов к экзамену по теории вероятностей и ма- тематической статистике. В каждом билете содержатся 3 воп- роса. Найти вероятность того, что в билете, который вытащит студентка, она будет знать ответы на все три вопроса. Введем 3 события: А1 = {студентка знает ответ на первый вопрос билета}. А 2 \А 1 = {студентка знает ответ на второй вопрос билета при выполнении события А1}. А 3 \А 1 × А 2 = {студентка знает ответ на третий вопрос биле- та при выполнении событий А1 и А2}.
Используя формулу (8.10) находим Вероятности Р (А 1); Р (А 2 \А 1); Р (А 3 \А 1 × А 2) находятся по формуле (8.4). Теперь получим правило сложения для совместных со- бытий. Если рассматриваемые события попарно несовместны, то для нахождения вероятности их суммы используется четвер- тая аксиома аксиоматического определения вероятности. Сначала рассмотрим правила сложения для двух совмест- ных событий. Теорема 8.1. Вероятность суммы двух совместных событий равна сумме их вероятностей минус вероятность их произве- дения, т. е. Р (А + В) = Р (А) + Р (В) — Р (А × В) (8.14) Доказательство этой теоремы не приводим, его можно най- ти в любом учебнике по теории вероятности, например [12, 46]. Используя формулу (8.14), получим правило сложения для трех совместных событий А1, А2, А3: Р (А 1 + А 2 + А 3) = Р (А 1 + А 2) + Р (А 3) − − Р ((А 1 + А 2) × А 3) = Р (А 1) + Р (А 2) − − Р (А 1 × А 2) + Р (А 3) − (Р (А 1 × А 3) + + Р (А 2 × А 3)) = Р (А 1) + Р (А 2) + Р (А 3) − Р (А 1 × А 2) − − Р (А 1 × А 3) − Р (А 2 × А 3) + Р (А 1 × А 2 × А 3). (8.15) Используя метод математической индукции, получим пра- вило сложения вероятностей для любого конечного количества совместных событий. Р (А 1 + А 2 + А 3 + … + А n) = Р (А 1) + + Р (А 2) + Р (А 3) + … + Р (А n) — (Р (А 1 × А 2) + + Р (А 1 × А 3) + … + Р (А n -1 × А n)) + + Р(А 1 × А 2 × А 3) + Р (А 1 × А 2 × А 4) + … + + Р (А × А × А)) + … + (-1) n -1 Р (А × А × … × А) (8.16) n |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 165; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.01 с.) |

 , (7.10)
, (7.10)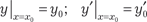 . (7.11)
. (7.11)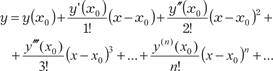 (7.12)
(7.12)


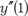

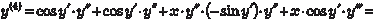
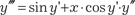
 и т. д.
и т. д.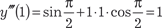
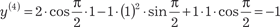 и т. д.
и т. д.
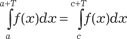
 , (7.13)
, (7.13)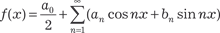 . (7.14)
. (7.14)


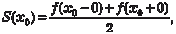

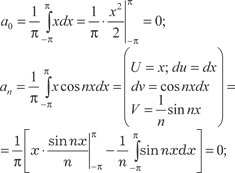

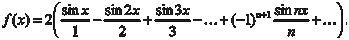
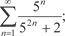 1.2.
1.2. 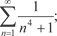
 1.4.
1.4. 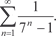

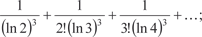
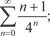

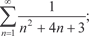
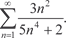
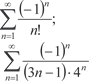 5.1.
5.1. 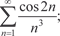 5.2.
5.2.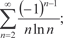 5.4.
5.4.
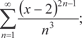

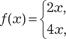
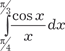
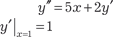 Используя метод последовательного дифференцирова- ния, найти приближенное частное решение дифференциально- го уравнения , если начальные условия имеют вид:
Используя метод последовательного дифференцирова- ния, найти приближенное частное решение дифференциально- го уравнения , если начальные условия имеют вид: 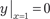 , .
, . , которое происходит тогда, когда не происходит собы- тие А.
, которое происходит тогда, когда не происходит собы- тие А. — промах.
— промах.
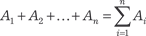


 = ∅.
= ∅.



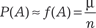 (8.2)
(8.2)
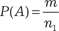
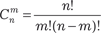


 Аксиоматическое определение вероятности. Как и другие разделы математики, теорию вероятностей можно развивать аксиоматическим методом.
Аксиоматическое определение вероятности. Как и другие разделы математики, теорию вероятностей можно развивать аксиоматическим методом. ;
;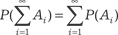 .
. .
. ) = 1, (8.6)
) = 1, (8.6)