Несобственный интеграл второго рода

Если на отрезке [ а, b ] функция у = f (х) имеет конечное количество точек разрыва первого рода, то дать определение интеграла для такой функции легко. В этом случае искомый интеграл есть сумма определенных интегралов, взятых по час- тичным интервалам, на которые разбивается отрезок [ а, b ] все- ми точками разрыва функции а < с 1 < с 2 … < с n < b, где с 1 с 2….. с n точки разрыва. Тогда будем иметь

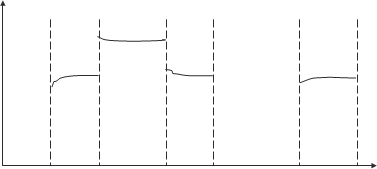
Таким образом, мы дали определение площади криво- линейной трапеции, соответствующей функции у = f (х) с ко- нечным числом точек разрыва первого рода на отрезке [ а, b ] (рис. 5.5).

Площадь этой трапеции есть сумма площадей трапеций, опирающихся на частичные интервалы [ а 1, с 1], [ с 1, с 2], ….[ с n, b ].

у

0           а     с 1                         с 2                   с 3                              с n                    b х

Рис. 5.5

Распространим определение интеграла на функции с бес- конечными разрывами.

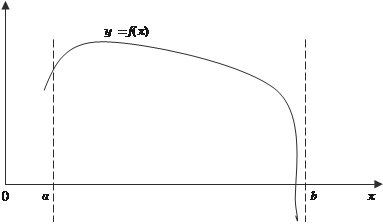
Пусть функция у = f (х) непрерывна для всех значений

а ≤ х < b, но в точке b имеет бесконечный разрыв (рис. 5.6).

у

Рис. 5.6

Поэтому определение интегралa в точке b теряет свой смысл. Но если взять обычный интеграл , то можно считать, что функция у = f (х) с уменьшением ε будет все лучше выражать ту величину, которую нужно взять в качестве интеграла от функции у = f (х) на отрезке [ а, b ].

Устремим ε к нулю, тогда I либо имеет предел, либо не име-

ет его (стремится к бесконечности либо не стремится ни к како- му пределу, колеблется).

Определение. Несобственным интегралом от функции у = f (х), непрерывной при а ≤ х < b и неограниченной при х → b, называется предел интеграла

.

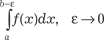Записывается это следующим образом:

.

Если данный предел существует, то несобственный интег- рал сходится, а если не существует, то расходится.

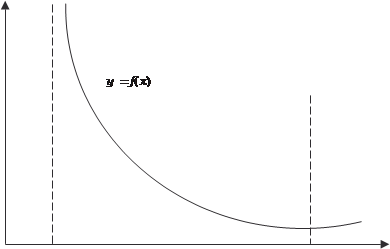
Аналогично дается определение несобственного интеграла   в том случае, если функция у = f (х) терпит бесконечный раз- рыв в левом конце отрезка интегрирования [ а, b ] (рис. 5.7).

 

у

0            а                                                         b          х

В этом случае имеем

Рис. 5.7

.

 

Если первообразную от функции у = f (х) можно найти, то искомый интеграл в обоих рассмотренных случаях находится по формуле

 

.

 

В том случае, если функция у = f (х) терпит бесконечный разрыв в какой-то промежуточной точке х = с отрезка интегри- рования [ а, b ], а < с < b (рис. 5.8), то согласно определению имеем

.

у

0

 

 

Рис. 5.8

Если оба интеграла в правой части последнего равенства сходятся, то сходится и интеграл

.

Если хотя бы один из интегралов в правой части расходит- ся, то расходится и исходный интеграл.

Теперь рассмотрим конкретные примеры.

Пример 5.38.

  — интеграл схо- дится.

Пример 5.39.

— интеграл расходится.

 

 

Некоторые приложения определенного интеграла