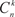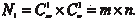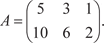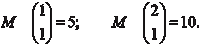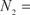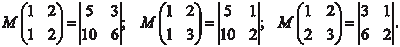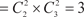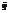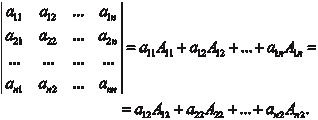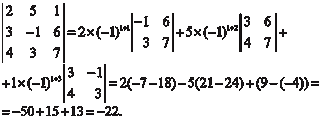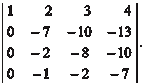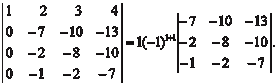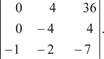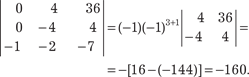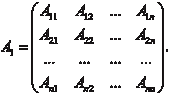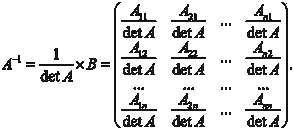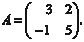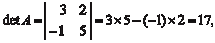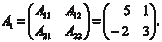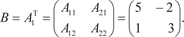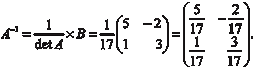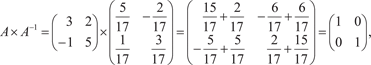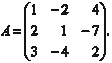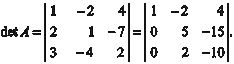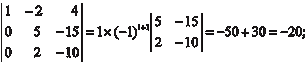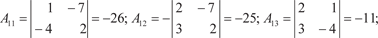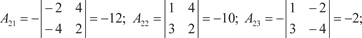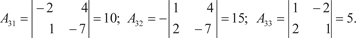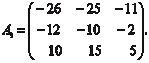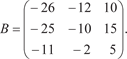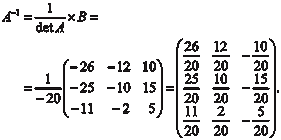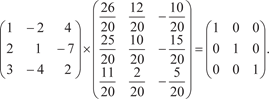Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матрицы, определители и их свойстваСодержание книги
Поиск на нашем сайте Матрицей называется прямоугольная таблица размером m (число строк) на n (число столбцов), заполненная некоторыми математическими объектами. Мы будем рассматривать матри- цы, элементами которых являются действительные числа.
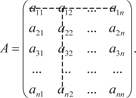
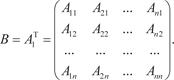
Как правило матрицы обозначают большими буквами (A, B,…), а их элементы маленькими буквами с двумя индексами, указывающими номер строки и номер столбца (a ij, b ij,…). Пря- моугольную матрицу размера m n записывают следующим образом: Если заменить строки матрицы ее столбцами (столбцы строками), то получим транспонированную матрицу, которую обозначают заглавной буквой с индексом T наверху:
Рассмотрим некоторые типы матриц. Если число строк матрицы равно числу ее столбцов, то мы имеем квадратную матрицу:
Элементы a 11, a 22, …, a nn называются главной диагональю, а их сумма — это след матрицы. Элементы a 1 n, a 2(n -1), …, a n 1 составляют побочную диагональ.
Если все элементы матрицы, кроме элементов, стоящих на главной диагонали, равны нулю, то мы имеем диагональную матрицу:
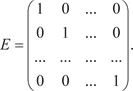
Если все ненулевые элементы диагональной матрицы рав- ны 1, то мы имеем единичную матрицу:
Если ненулевые элементы располагаются выше главной диагонали, то имеем верхнюю треугольную матрицу, а если ниже — нижнюю треугольную матрицу:
Матрица размера m 1 — это матрица-столбец, а матрица размера 1 n — матрица-строка:
Рассмотрим линейные операции над матрицами. Для сложения двух матриц необходимо, чтобы они имели одинаковые размеры. Сумму двух матриц обозначим A + B, а ее элементы равны
a ij + b ij, т. е.
Сложение матриц обладает следующими свойствами: 1) A + B = B + A; 2) (A + B) + C = A + (B + C); 3) Для любых двух матриц одинакового размера всегда су- ществует единственная матрица Z такая, что A + Z = B. Тогда Z есть разность матриц B и A, т. е. Z = B − A. Элементы матрицы Z равны b ij − a ij.
Для умножения двух матриц необходимо, чтобы они были согласованными. Матрицы A и B называются согласованными, если число столбцов матрицы A равно числу строк матрицы B.
Пусть заданы матрицы:
Тогда произведением матрицы A на матрицу B называется матрица C размера m p, элементы c ik которой находятся по формуле Из определения произведения матриц следует, что A E = E A = A. Произведение матриц обладает следующими свойствами: 1) (A B) C = A (B C); 2) (A + B) C = AC + BC; 3) k (A · B) = (k · A) · B, k ∈ R; 4) (A · B)T = B T · A T. В общем случае A B B A.
Рассмотрим конкретный пример умножения двух матриц Для квадратной матрицы размера n n вводится понятие определителя. Определителем квадратной матрицы порядка n n (оп- ределителем порядка n) называется алгебраическая сумма всевозможных произведений элементов матрицы, взятых по одному из каждой строки, по одному из каждого столбца и снаб- женных знаками плюс и минус по некоторому определенному правилу. Это правило сформулируем позже.
Определитель порядка n матрицы обозначается следующим образом:
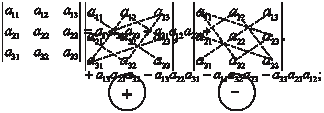
Например,
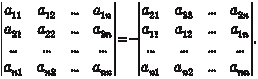
Сформулируем свойства определителей. 1. При транспонировании матрицы ее определитель не ме- няется. 2. При перестановке строк (столбцов) знак определителя меняется на противоположный:
3. Если все элементы строки (столбца) матрицы равны нулю, то ее определитель равен нулю:
4.
где
5. Определитель равен нулю, если все элементы минимум двух его строк (столбцов) пропорциональны:

6. Если каждый элемент строки (столбца) определите- ля есть сумма двух слагаемых, то такой определитель можно представить в виде суммы двух определителей, у одного из ко- торых соответствующая строка (столбец) составлена из первых слагаемых суммы, а у другого — из вторых:
7. Значение определителя не изменится, если к элементам его строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же вещест- венное число:
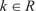
(R — множество действительных чисел).
Дадим понятие минора и алгебраического дополнения. Рассмотрим матрицу размера m n: Выделим в ней k различных строк и k различных столбцов, причем 1 k минимального значения из m и n. Элементы выделенных строк и столбцов образуют квад- ратную матрицу порядка k. Определитель выделенной квад- ратной матрицы порядка k называют минором k -го порядка матрицы А. Если в выделенную квадратную матрицу порядка k вклю- чены строки и столбцы исходной матрицы, имеющие одинако- вые номера, то такой минор называется главным.
Полное обозначение минора k -го порядка следующее где i — номера выделенных строк; j — номера выделенных столбцов.
Общее число миноров порядка k прямоугольной матрицы размера m n можно найти по формуле где
Число миноров первого порядка совпадает с общим числом элементов исходной матрицы Рассмотрим конкретный пример
Общее число миноров первого порядка данной матрицы А
равно 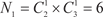 . Например, . Например,
Максимальный порядок миноров данной матрицы равен двум. Общее число миноров второго порядка равно
Рассмотрим теперь квадратную матрицу размера n n
Вычеркнем в ней все элементы i -й строки и j -го столбца. Оставшиеся элементы образуют квадратную матрицу размера (n −1) (n −1). Определитель этой матрицы будет минором (n −1) порядка исходной матрицы А. Например, вычеркнем в матрице А первую строку и вто- рой столбец и получим следующий минор (n −1) порядка исход- ной матрицы
Минор обозначаем по номеру элемента, который стоит на пересечении вычеркиваемой строки и вычеркиваемого столб- ца. В нашем случае это элемент a 12. Алгебраическим дополнением элемента a ij квадратной матрицы порядка n называется число, вычисляемое по фор- муле A ij = (−1) M, т. е., если сумма номеров строки и столб-
i+j ца — четная, алгебраическое дополнение будет совпадать с со- ответствующим минором, а если нечетная, то алгебраическое дополнение и минор будут иметь разные знаки. Используя понятие алгебраического дополнения можно сформулировать общее правило вычисления определителя n -го порядка. Он вычисляется с помощью формул разложения по элементам какой-либо строки или какого-либо столбца. Все- го существует 2 n формул разложения определителя (по эле- ментам n -строк и n -столбцов). Например, приведем разложение по элементам первой строки и второго столбца:
То есть каждый элемент строки (столбца) умножается на соответствующее алгебраическое дополнение. Теоретически с помощью формул разложения можно вы- числить определитель квадратной матрицы любого порядка, но реально эти формулы используются для нахождения определи- телей не выше 4-го порядка. Объем вычислений можно несколь- ко сократить, если использовать свойства определителей. Из формул разложения следуют приведенные нами выше правила вычисления определителей второго и третьего по- рядков. Рассмотрим конкретные примеры вычисления определи- телей.
В данном примере мы разложили определитель по элемен- там первой строки.
Найдем определитель 4-го порядка К этому определителю сначала применим свойство но- мер 7. Первую строку определителя умножим последователь- но на (−4); (−3); (−2) и сложим со 2-й; 3-й и 4-й строками. В ре- зультате получим
Полученный определитель разложим по элементам 1-ого столбца
К полученному определителю вновь применим свойство номер 7. Умножим последовательно третью строку на (−2) и на (−7) и сложим со второй и первой строчками. Получим
Последний определитель разложим по элементам первого столбца, т. е.
Теперь рассмотрим обратную матрицу и правило ее вы- числения. Квадратная матрица А называется вырожденной, если ее определитель равен нулю, т. е. det A = 0. В противоположном случае (det A 0) матрица А является невырожденной. А любой невырожденной матрице А соответс- твует единственная обратная матрица A −1. Причем выполняется равенство A − 1 A = A A − 1 = E. Приведем алгоритм нахождения обратной матрицы. 1. Вычислить определитель матрицы А и убедиться, что он не равен нулю. 2.
Составить матрицу A 1 из алгебраических дополнений матрицы А. 3. Составить присоединенную матрицу (В), получаемую транспонированием матрицы A 1
4.
Вычислить обратную матрицу по формуле 5. Проверка полученного результата A A − 1 = A − 1 A = E. Рассмотрим конкретные примеры на обращение матриц. Пример 2.1. Дано:
Найти: A −1
Находить A −1 будем в соответствии с приведенным алго- ритмом. Найдем определитель исходной матрицы т. е. det A 0, поэтому у матрицы А есть обратная A −1 Теперь найдем алгебраическое дополнение: A 11 = 5; A 12 = 1; A 21 = − 2; A 22 = 3.
Составим из найденных алгебраических дополнений мат- рицу A 1 Найдем матрицу В (транспонируем матрицу А 1)
Вычисляем обратную матрицу Проверим правильность вычисления обратной матрицы.
т. е. обратная матрица А −1 вычислена верно.
Пример 2.2. Дано: Найти A −1.
Вычисляем определитель матрицы А. Умножаем первую строку последовательно на (−2) и на (−3) и складываем со второй и третьей, затем полученный опреде- литель раскладываем по элементам первого столбца
det A 0, т. е. исходная матрица А — невырожденная и у нее есть обратная матрица. Теперь найдем алгебраические дополнения всех элемен- тов матрицы А
Из найденных алгебраических дополнений составляем матрицу A 1
 : :
Вычисляем обратную матрицу Делаем проверку правильности вычисления обратной мат- рицы A A −1 = E
Из проверки следует, что обратная матрица вычислена верно. Имеют место следующие равенства: det A − 1 = (det A) − 1; (A − 1) T = (A T) − 1; (A B C … F) − 1 = F − 1 … C − 1 B − 1 A − 1. Ранг матриц. Любая матрица кроме своего порядка должна характеризоваться еще одним показателем, который устанав- ливает количество ее лтнейно-независимых строк и столбцов. Этот показатель и называют рангом матрицы. Дадим его опре- деление. Рангом (r (A)) матрицы А называют наивысший порядок от- личных от нуля миноров этой матрицы. Ранг имеет любая мат- рица. Ранг матрицы считается равным нулю, если все элементы матрицы равны нулю. Для матриц высокого порядка разработаны специальные вычислительные методы определения ранга, например, мето- ды жордановых исключений. Из приведенных выше свойств определителей следует, что ранг матрицы не изменяется при ее транспонировании, при перестановке каких-либо строк или столбцов, при умножении каждого элемента строки или стол- бца на одно и то же число, при сложении элементов какой-то строки (столбца) с соответствующими элементами другой стро- ки (столбца), умноженными на действительное число. Без доказательства приведем теорему и следствия из нее. Теорема 2.1. Если ранг матрицы равен k, то существует k линейно-независимых строк, от которых линейно зависят все остальные строки матрицы. Следствие 1. Если ранг матрицы равен k, то она имеет k линейно-независимых столбцов, от которых линейно зависят остальные столбцы. Следствие 2. Максимальное число линейно-независимых строк матрицы совпадает с максимальным числом линейно-не- зависимых столбцов и равно рангу матрицы.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 155; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

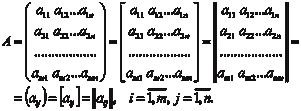
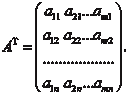
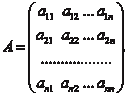
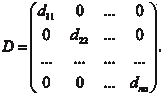
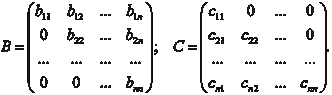
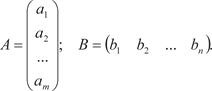
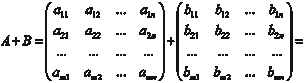
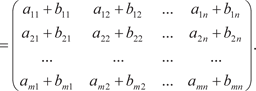
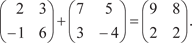
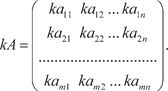
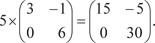
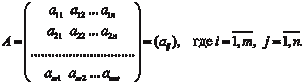
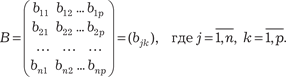
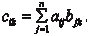
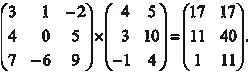
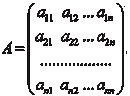
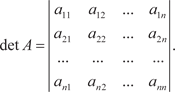
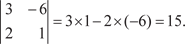
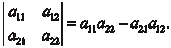
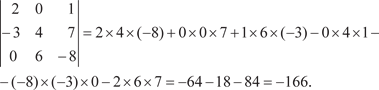
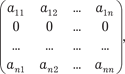
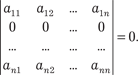
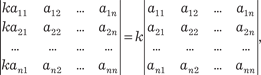
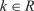 (R — множество дейст- вительных чисел).
(R — множество дейст- вительных чисел).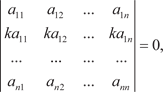

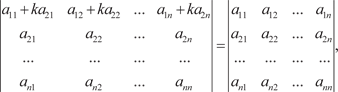
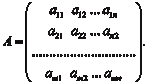
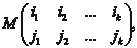
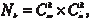
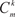 — число сочетаний из m по k,
— число сочетаний из m по k,