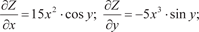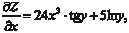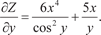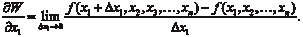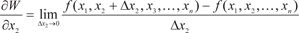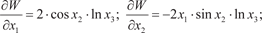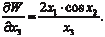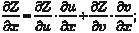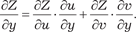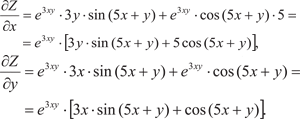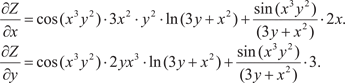Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Некоторые сведения о функциях многих переменных. Понятие о частной производной
Ранее были рассмотрены функции, которые зависели от одного независимого аргумента. Но в реальной действительнос- ти чаще приходится иметь дело с функциями, которые зависят от двух, трех и большего числа независимых аргументов. Например, площадь прямоугольника со сторонами а и b бу- дет функцией двух независимых аргументов. Функция эта име- ет вид S пр = a · b, где a и b могут быть любыми действительными положительными числами, так как и стороны прямоугольника, и его площадь не могут быть отрицательными величинами. Положение какого-либо объекта на поверхности планеты определяется тремя координатами: широтой, долготой и высо- той, т. е. является функцией трех независимых аргументов.
Положение космического аппарата (КА), движущегося по невозмущенной эллиптической орбите вокруг Земли, есть фун- кция шести аргументов (трех координат (x, y, z) и трех состав- ляющих скорости 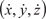 ). Эта функциональная зависимость имеет следующий вид: ). Эта функциональная зависимость имеет следующий вид:
В гуманитарных науках, например в юриспруденции и экономике, жестко детерминированные функциональные свя- зи встречаются нечасто. Там используются многофакторные статистические взаимосвязи вида Z = f(x 1, x 2, …, x n) + f(x 1, x 2, …, x n) + (y 1, y 2, …, y m). где x 1, x 2, …, x n — учтенные признаки, под влиянием которых меняется функция Z, x 1, x 2, …, x n — ошибки учтенных признаков, y 1, y 2, …, y m — неучтенные признаки, которые могут влиять на функцию Z. Сначала рассмотрим функцию двух независимых аргу- ментов х и у. Переменная величина Z называется функцией переменных величин х и у на множестве D, если каждой точ- ке этого множества соответствует одно определенное значение величины Z. Множество D называется областью определения функции Z. Обычно она представляет собой часть плоскости х 0 у, ограни- ченной одной или несколькими линиями. Тот факт, что Z есть функция независимых аргументов х и у записывают так: Z = f(x, y). Функция двух аргументов может задаваться следующими способами: 1)
 аналитическим, т. е. приводится формула, при помощи которой по заданным значениям аргументов х и у находят зна- чения функции Z. Например, аналитическим, т. е. приводится формула, при помощи которой по заданным значениям аргументов х и у находят зна- чения функции Z. Например,
2) табличным, т. е. для некоторого количества пар аргумен- тов (х, у) приводятся значения функции (Z).
3) графическим.
Графиком функции двух независимых аргументов в сис- теме прямоугольных координат называется множество точек,
Рис. 4.4 абсциссы и ординаты которых являются значениями х и у, а ап- пликаты — соответствующими значениями Z. Графиком функ- ции двух непрерывных аргумен- тов обычно служит поверхность. Например, графиком функции Z = x 2 + y 2 является параболоид вращения (рис. 4.4).
ментов x, x, …, x. 1 2 n Переменная величина W называется функцией перемен- ных величин x 1, x 2, …, x n, если каждой рассматриваемой сово- купности этих величин соответствует одно определенное зна- чение W. Тот факт, что W есть функция аргументов x 1, x 2, …, x n, за- писывают так: W = f (x 1, x 2, …, x n). Геометрическая иллюстрация функций от n независимых аргументов теряет наглядность при n > 2. При исследовании поверхностей 2-го порядка часто приме- няют метод сечений, который заключается в том, что определе- ние вида поверхности по ее уравнению производится путем изу- чения кривых, образованных при пересечении этой поверхности плоскостями, параллельными координатным плоскостям. Дадим определение предела функции двух независимых аргументов. Число b называется пределом функции Z = f (x, y) при x → x 0 и y → y 0, если для всех значений х и у, достаточно мало отличающихся от x 0 и y 0, соответствующие значения функции f (x, y) как угодно мало отличаются от числа b. Тот факт, что b есть предел функции Z = f (x, y) при x → x 0 и y → y 0 записывают так:
Теперь введем понятия частных производных по незави- симым аргументам. Рассмотрим функцию двух независимых аргументов х и у Z = f (x, y). Предположим, что y = const и рассмотрим f (x, y) как фун- кцию одного независимого аргумента х.
Если эта функция дифференцируема, то существует предел Нижний индекс (х) указывает на то, что производная бе- рется по аргументу х. Частной производной по х от функции Z = f (x, y) называ- ется функция переменных величин х и у, которая получается при дифференцировании f (x, y) по х в предположении, что y = const.
Она обозначается так: Аргумент у считается постоянным только в процессе диф- ференцирования. После нахождения частной производной функция
Аналогично определим частную производную по у от фун- кции Z = f (x, y) при x = const. Как предел Она обозначается так: Пример 4.6. Z = 5 x 3 · cos y.
Пример 4.7.
Z = 6 x 4 · tg y + 5 x · ln y,
Аналогично можно определить частные производные от любого числа независимых аргументов. Например, имеем функцию n независимых переменных W = f (x 1, x 2, …, x n)
Определим частную производную по аргументу x 1 Аналогично определим частную производную по аргумен- ту x 2
и так далее. Пример 4.8. W = 2 x 1 · cos x 2 · ln x 3;
Дифференцирование сложных функций Пусть имеем функцию двух независимых аргументов Z = f (u, v), причем аргументы являются функциями независи- мых переменных х и у, т. е. u = (x, y); v = (x, y), следовательно Z = f [ (x, y), (x, y)].
В этом случае частные производные функции Z по аргу- ментам х и у будут вычисляться по формулам.
Пример 4.9. Z = e 3xy · sin (5 x + y).
Пример 4.10.
Z = sin (x 3 y 2)·ln (3 y + x 2).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 102; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.168.16 (0.011 с.) |
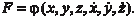
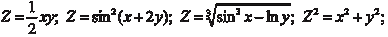
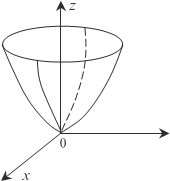
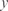
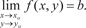
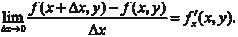
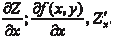
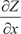 будет зависеть от двух аргументов х и у.
будет зависеть от двух аргументов х и у.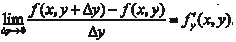
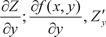 . При нахождении частных производных используются формулы и правила диф- ференцирования функции одного независимого аргумента. Рассмотрим конкретные примеры.
. При нахождении частных производных используются формулы и правила диф- ференцирования функции одного независимого аргумента. Рассмотрим конкретные примеры.