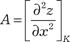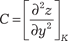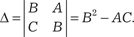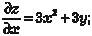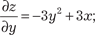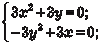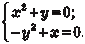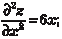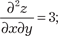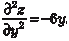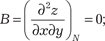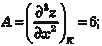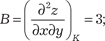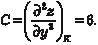Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Экстремумы функций двух и многих аргументовСодержание книги
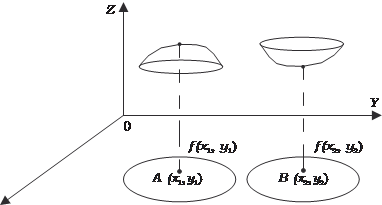
Поиск на нашем сайте Понятие экстремума функции двух аргументов аналогич- но соответствующему понятию функции одного аргумента. Пусть функция Z = f (х, y) определена в некоторой области D плоскости Х0Y, а точки А(х 1, y 1) и В (х 2, y 2) принадлежат D. Определения. Точка А (х 1, y 1) есть точка максимума функ- ции Z = f (х, y), если f (х 1, y 1) является наибольшим значением функции Z = f (х, y) в некоторой окрестности точки А (х 1, y 1). Аналогично, точка В (х 2, y 2) есть точка минимума функции Z = f (х, y), если f (х 2, y 2) является наименьшим значением функ- ции Z = f (х, y) в некоторой окрестности точки В (х 2, y 2). Часто говорят, что функция Z = f (х, y) достигает в точках А (х 1, y 1) и В (х 2, y 2) экстремума. Заметим, что экстремум функции двух аргументов всегда лежит внутри области определния функции (это следует из оп- ределния). Точки максимума и минимума функции двух аргументов показаны на рис. 4.21.
Рис. 4.21 Приведем необходимое условие экстремума функции двух независимых аргументов.
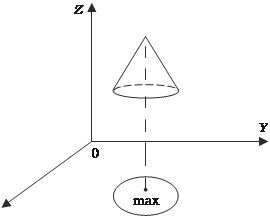
Теорема 4.7. Если в точке С (х 0, y 0) дифференцируемая функция Z = f (х, y) имеет экстремум, то ее частные производ- ные в этой точке равны нулю, т. е. Точка С (х 0, y 0), в которой частные производные функции Z = f (х, y) обращаются в ноль, называется стационарной точ- кой функции Z = f (х, y). Геометрически необходимый признак означает, что в экст- ремальной точке касательная плоскость к поверхности парал- лельна плоскости Х0Y. Точками экстремума непрерывной функции двух аргумен- тов могут быть точки, в которых функция недифференцируе- ма. Этим точкам соответствуют острия поверхности графика функции Z = f (х, y) (рис. 4.22).
Рис. 4.22 Например, функция Следовательно, точками экстремума функции двух аргу- ментов могут быть точки, где либо одновременно f ′ х (х, y) = 0, f ″ y (х, y) = 0, либо хотя бы одна из этих частных производных не существует. Точки этих двух типов называют критическими. Аналогично определяется экстремум функции любого числа независимых аргументов W = f (х 1, х 2, …, х n) и вводятся необходимые условия экстремума.
Поэтому для нахождения экстремумов имеем систему n уравнений с n неизвестными. Однако не любая критическая точка является точкой экс- тремума. Пример 4.32.
0, у = 0. Но экстремума в этой точке нет. Действительно, Z (0, 0) = 0, а в любой окрестности точки А (0, 0) можно найти и положительные и отрицательные значе- ния функции. Данная функция Z = ху называется гиперболи- ческим параболоидом и имеет вид седла. Приведем достаточный признак экстремума для функции двух аргументов. Он имеет гораздо более сложный вид, чем для функции одного аргумента. Теорема 4.9. Пусть в стационарной точке К (х 0, y 0) и в неко- торой ее окрестности функция Z = f (х, y) имеет непрерывные частные производные до второго порядка включительно. Най- дем в точке К (х 0, y 0) значения:
а) если ∆ < 0, то функция Z = f (х, y) имеет в точке К (х 0, y 0) экстремум: максимум при А < 0, С < 0 и минимум при А > 0, С > 0 (из условия ∆ < 0 следует, что А и С всегда имеют одина- ковые знаки); б) если ∆ > 0, то точка К (х 0, y 0) не является точкой экстре- мума функции Z = f (х, y); в) если ∆ = 0, то экстремум в точке К (х 0, y 0) может быть, а может и не быть и для определения его нужны дополнитель- ные исследования. Пример 4.33 Найти экстремумы функции Z = x 3 − у 3 + 3 ху − 5. Используем необходимый признак экстремума и полу-
чим:
Далее находим х = у 2, поэтому у 4 + у = 0, или у (у 3 + 1) = 0. Из последнего выражения находим у = 0 или у = -1 (комплекс- ные корни не учитываем). Поэтому получаем две стационарные точки: N (0, 0) и К (1, -1).
Для того, чтобы определить, будут ли найденные точки экстремумами исходной функции, применим достаточный при- знак экстремума. Тогда получим:
Рассмотрим точку N (0, 0). Найдем:
Тогда ∆ = B 2 − АС = 9 > 0, т. е. точка N (0, 0) не является точ- кой экстремума исходной функции.
Рассмотрим точку К (1, -1). Найдем:
Тогда ∆ = В 2 − АС = -27 < 0, т. е. точка К (-1, 1) будет точкой экстремума исходной функции, а так как А > 0 и С > 0, то это точка минимума и значение функции в этой точке равно -6 (Z min = -6).
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 190; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |

 Х
Х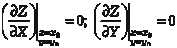
 Х
Х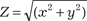 имеет минимум в начале координат, но в этой точке функция недифференцируема. Дан- ная функция представляет собой круглый конус с вершиной в начале координат.
имеет минимум в начале координат, но в этой точке функция недифференцируема. Дан- ная функция представляет собой круглый конус с вершиной в начале координат.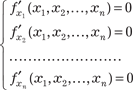
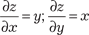 Для функции Z = х · y точка А (0, 0) будет критической, так как и по необходимому признаку экстремума х =
Для функции Z = х · y точка А (0, 0) будет критической, так как и по необходимому признаку экстремума х =