Дифференциальные уравнения, сводящиеся к однородным дифференциальным уравнениям первого порядка
Дифференциальное уравнение
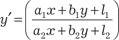 . (6.6) . (6.6)
можно свести к однородному дифференциальному уравнению. Возможны два случая:
1) .
Делаем замену
(6.7)
где t и k постоянные.
После замены дифференциальное уравнение (6.6) прини- мает следующий вид:
 (6.8) (6.8)
Для того чтобы полученное дифференциальное уравне- ние стало однородным, необходимо выполнение следующих условий:
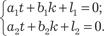 (6.9) (6.9)
Из решения системы (6.9) получим неизвестные постоян- ные t и k, подставим их в (6.8) и получим однородное диффе- ренциальное уравнение, метод решения которого мы рассмат- ривали ранее.
2)  . .
В этом случае используем подстановку a 1 x + b 1 y = p, с по- мощью которой исходное дифференциальное уравнение сво- дится к дифференциальному уравнению с разделяющимися переменными.
Пример 6.6.
Найти общее решение дифференциального уравнения. (2 x – y + 1) dx + (- x + 2 y - 1) dy = 0;
(x - 2 y + 1) dy = (2 x – y + 1) dx.
,
т. е. имеем первый случай. Делаем замену переменной:
Тогда исходное дифференциальное уравнение примет вид:
. (6.10)
Неизвестные постоянные t и k найдем из решения системы:
Умножаем второе уравнение системы на (-2) и складываем с первым: 3 k − 1 = 0.
Поэтому k = 1/3.
Из второго уравнения системы находим t = 2 k − 1 = 2/3 − 1 =
= -1/3.
Подставляем найденные значения k и t в уравнение (6.10) и получаем
.
Из сделанной нами замены переменных следует, что dx = du, а dy = dv. Поэтому имеем:
.
Полученное дифференциальное уравнение является одно- родным. Для его решения сделаем еще одну замену, обозначим z = v / u. Далее получаем v = z · u.
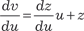 . .
После подстановки однородное дифференциальное урав- нение принимает вид:
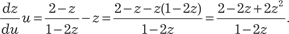
Полученное дифференциальное уравнение является диф- ференциальным уравнением с разделяющимися переменными. Разделяем переменные и получаем:
Интегрируем обе части последнего выражения: Далее получаем:

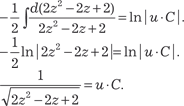
Делаем обратную подстановку и получаем:
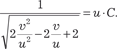
Теперь надо возвратиться к переменным y и x. Учитывая, что u = x + 1/3, а v = y − 1/3, получаем:
Последнее выражение и есть общий интеграл исходного дифференциального уравнения.
Пример 6.7.
Найти общее решение дифференциального уравнения.
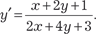
,
т. е. имеем второй случай.
Исходное дифференциальное уравнение представляется в виде
Делаем замену x + 2 y = p, дифференцируем р по аргумен- ту х и получаем:
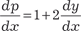 . .
Далее имеем: 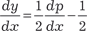 . .
После подстановки исходное дифференциальное уравне- ние принимает вид:
.
,
т. е. получили дифференциальное уравнение с разделяющими- ся переменными. Разделяя их, получаем:
.
Интегрируем обе части последнего выражения и получаем: 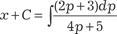 . .
Для взятия интеграла делим числитель подынтегрального выражения на знаменатель, т. е.
 – 2р + 3 4р + 5 – 2р + 3 4р + 5
2р + 2,5 1/2
1/2
Поэтому получаем:
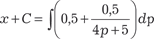 ; ;
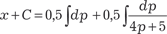 ; ;
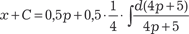 ; ;
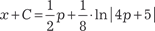 . .
Делаем обратную замену и получаем:
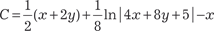 . .
Полученное выражение и есть общий интеграл исходного дифференциального уравнения.
|