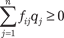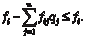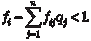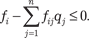Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод Гомори для полностью целочисленных задачСодержание книги
Поиск на нашем сайте Необходимым условием применения этого алгоритма яв- ляется целочисленность всех коэффициентов и правых частей ограничений. Невыполнение этого условия не позволяет по- лучить целочисленного решения. Дело в том, что требование целочисленности распространяется и на дополнительные пе- ременные задачи ЦЛП, а наличие дробных коэффициентов в ограничениях приводит к нарушению этого требования. Рассмотрим алгоритм решения полностью целочисленной задачи ЛП. 1. Решение задачи линейного программирования без учета условий целочисленности переменных. Такая задача ЛП называ- ется задачей с ослабленными ограничениями. Если все базисные переменные задачи целочисленны, то решение считается полу- ченным и выполнение дальнейших процедур не имеет смысла. 2. Формирование уравнения отсекающих плоскостей Го- мори. Из итоговой симплекс-таблицы выбираются строки, ко- торые соответствуют нецелочисленным значениям базисных переменных. Такие строки называются производящими. Все последующие действия основаны на том положении, что любое нецелое число может быть представлено в виде суммы ближай- шего наибольшего целого числа и дробной части: α = [α] + f,
Производящую строку записывают в виде следующего уравнения:
где βi — нецелое число, расположенное в столбце “Решение”, qj — дополнительная (остаточная или избыточная) пере- менная, αij — коэффициент при дополнительной переменной. Фигурирующие в этом уравнении величины αij и βi пред- ставляют также в виде суммы целого и дробного чисел: αij = [αij] + f ij, 0 ≤ f ij < 1; βi = [βi] + f i, 0 ≤ f i < 1. После подстановки в исходное уравнение получают следу- ющее выражение:
После переноса вправо целых частей уравнение приобре- тает следующий вид:
Так как xi и qj должны быть целочисленными, то правая часть этого выражения также должна быть целочисленной. Но исходя из имеющегося равенства следует вывод о том, что и левая часть этого выражения тоже должна быть цело- численной.
лению дробного числа, то . Из этого следует, что левая часть последнего равенства может быть представлена в виде
Учитывая то условие, что 0 < fi < 1, неравенство приобре- тает вид Левая часть этого неравенства не может быть равной 1, по- этому, делая логическое заключение, можно записать:
Это неравенство является выражением необходимого ус- ловия целочисленности и одновременно его можно рассматри- вать как дополнительное ограничение задачи линейного про- граммирования.
В соответствии с процедурами решения задачи ЛП нера- венство (9.3) приводится к стандартному виду введением оста- точной переменной sn+1: Из нескольких производящих строк, имеющихся в итого- вой симплекс-таблице, выбирается та, которая характеризует- ся максимальным значением дробной части базисной перемен- ной fi. Величина fi определяет вклад дробной части в приближе- ние решения задачи ЦЛП к оптимальной целочисленной точке ОДР: чем больше дробная часть, тем ближе значение базисной переменной к целочисленному оптимальному решению. После выбора производящей строки формируется уравне- ние отсечения:
Такая форма представления уравнения необходима для удобства его записи в итоговую симплекс-таблицу. Это ограни- чение-равенство определяет отсечение Гомори для полностью целочисленных задач. Уравнение (9.4) является математической формой описания плоскости, отсекающей от ОДР ту ее часть, которая не содержит целочисленных значений. Это уравнение можно получить, вы- разив небазисные переменные qj из исходных ограничений стан- дартной задачи ЛП и подставив их в уравнение (9.4). 3. Формирование и решение дополнительной задачи ЛП. Для решения этой задачи используется двойственный симплекс-метод, описанный в подразд. 9.4. Результатом решения дополнительной задачи ЛП может быть целочисленное значение всех переменных, тогда задача считается решенной, В противном случае осуществляется пе- реход к п. 2 алгоритма. Количество шагов в методе отсечений Гомори не может быть больше количества переменных исходной задачи, куда входят как переменные задачи линейного программирования (ЗЛП), так и дополнительные переменные (n + m). Пример 9.11. Рассмотрим следующую задачу ЦЛП: Найти max Z = x1 + 2x2 при ограничениях: 3/2x1 + 1/2x2 ≤ 7/2, x1 + 3x2 ≤ 7, x1, x2 ≥ 0, целые. Решение. Учитывая требование целочисленности коэффициентов при переменных в линейных ограничениях, необходимо обе части первого ограничения умножить на наименьший общий знаменатель. В результате выполнения этой процедуры исход- ная задача ЦЛП приобретает вид: найти max Z = x1 + 2x2 при ограничениях: 3x1 + x2 ≤ 7, x1 + 3x2 ≤ 7, x1, x2 ≥ 0, целые. После приведения к стандартному виду задача представ- ляется следующим образом: найти max Z = x1 + 2x2 при ограничениях: 3x1 + x2 + s1 = 7; x1 + 3x2 + s2 = 7; x1, x2, s1, s2 ≥ 0, целые. Решение этой задачи без учета целочисленности перемен- ных, т. е. задачи с ослабленными ограничениями, приводит к следующей итоговой симплекс-таблице (табл. 9.12).
Таблица 9.12
Как видно из таблицы, базисные переменные имеют не- целочисленные значения, поэтому следующим шагом явля- ется формирование отсекающей плоскости Гомори, для чего из симплекс-таблицы выбирается производящая строка. По- скольку при целочисленных значениях переменных значение ЦФ тоже будет целочисленным, то в качестве производящей строки может выбираться и Z-строка симплекс-таблицы. Вы- бор строки осуществляется по максимуму дробной части fi тех чисел, что представлены в столбце “Решение”. В данном случае максимальные и равные значения дробной части f1 = f2 = 3/4 имеют числа, соответствующие базисным переменным x1 и x2. Поэтому любая из этих строк может быть выбрана в качестве производящей. Допустим, в качестве производящей выбрана строка, соответствующая базисной переменной x1. Отсечение Гомори строится на основании равенства (9.4): s3 = 3/8s1 − 1/8s2 − 3/4, или s3 − 3/8s1 + 1/8s2 = -3/4. Подстановка этого уравнения в итоговую симплекс-табли- цу и последующее выполнение итераций двойственного симп- лекс-метода приводят к таблице с целочисленными значения- ми базисных переменных (табл. 9.13): Таблица 9.13
В том, что составленное выше отсечение Гомори действи- тельно исключает некоторые области многогранника допусти- мых решений, можно убедиться следующим образом. Для этого в уравнение отсечения Гомори вместо переменных s1 и s2 необ- ходимо подставить их выражения, полученные из ограничений стандартной задачи ЛП: s3 − 3/8(7 − 3x1 − x2) + 1/8(7 − x1 − 3x2) = − 3/4 или s3 + x1 = 1. Это уравнение эквивалентно неравенству x1 ≤ 1, которое может рассматриваться как дополнительное, третье, ограничение исходной задачи ЦЛП. Графическое решение задачи представлено на рис. 9.4. Жирными точками на рисунке показаны точки ОДР, харак- теризующиеся целочисленными значениями переменных, а штриховой линией — линия, соответствующая третьему ог- раничению. Как видно, этим ограничением от ОДР отсекает- ся та ее часть, которая не содержит целочисленных значений переменных (на рисунке она заштрихована). Оптимальное це- лочисленное решение рассматриваемой задачи достигается в точке Е.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 228; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.152 (0.007 с.) |


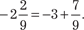
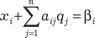
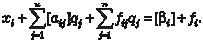
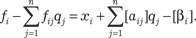 (9.2)
(9.2)