
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод Гомори для частично-целочисленных задач
Для частично-целочисленных задач характерно то, что требование целочисленности накладывается только на часть
Рис. 9.4. Графический метод решения задач
переменных. В целом последовательность решения этих задач такова же, как и полностью целочисленных задач, а именно: 1) решается задача ЦЛП с ослабленными ограничениями; 2) на основе итоговой симплекс-таблицы выбирается производящая строка и формируется уравнение отсечения Гомори; 3) решается дополнительная задача ЛП с применением двойственного симплекс-метода. Различие с первым алгорит- мом состоит лишь в способе формирования уравнения отсече- ния Гомори.
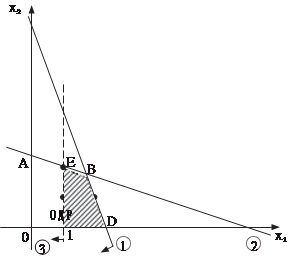
Допустим, что получено решение задачи ЦЛП с ослаблен- ными ограничениями. Из итоговой симплекс-таблицы выписы- вается производящая строка для той переменной xk, на кото- рую наложено требование целочисленности: где qj — небазисная переменная, на которую в общем случае условие целочисленности может быть и не наложено. Правую часть равенства представляют в виде суммы це- лой и дробной частей числа:
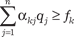 ; ;
если же xk ≥ [βk] + 1, тогда . Поскольку нецелочисленные коэффициенты αkj могут быть как положительными, так и отрицательными, то их разделяют следующим образом. Вводят J+ — множество индексов j, для которых αkj ≥ 0, и J — множество индексов, для которых α < 0.
После небольших преобразований: либо составляют совместное уравнение
либо, добавляя остаточную переменную, формируют уравне- ние отсекающей плоскости: Это уравнение определяет искомое отсечение Гомори для частично-целочисленных задач и представляет собой необхо- димое условие целочисленности переменной xk. Далее решается дополнительная задача ЛП (с расширен- ной симплекс-таблицей) двойственным симплекс-методом и определяется целочисленное значение рассматриваемой пере- менной. Основным недостатком метода отсекающих плоскостей Гомори является невозможность решения целочисленных за- дач большой размерности.
Метод ветвей и границ Этот метод так же, как и метод отсечений Гомори, приме- ним для решения как полностью, так и частично-целочислен- ных задач и тоже основан на первоначальном решении задачи ЛП с ослабленными ограничениями. Идея метода основана на переборе всех возможных комбинаций целочисленных значе- ний переменных задачи. Однако при большой размерности за- дачи ЦЛП подобный перебор может потребовать много времени, а иногда и вообще невозможен. Рациональность этого процесса обеспечивается рядом процедур, которые существенно снижа- ют количество просматриваемых комбинаций.
Процесс решения задачи состоит из нескольких последо- вательно выполняемых шагов. 1. Решение задачи ЛП с ослабленными ограничениями. Если ЦФ и переменные удовлетворяют требованию целочис- ленности, то полученное решение рассматривается в качестве оптимального. В противном случае переходят к шагу 2. 2. Формирование ветвей исследования. Допустим, условию целочисленности не удовлетворяют переменные xk, xr. Тогда на основе дробного значения, например, xk формируются две не связанные между собой подзадачи: а) xk ≤ [xk]; б) xk ≥ [xk] + 1. В общем случае выбор переменной, на основе которой ор- ганизуется процесс ветвления, влияет на эффективность ре- шения задачи. Для такого выбора существуют специальные эмпирические или эвристические процедуры. 3. Решение подзадачи а). Решение осуществляется на осно- ве итоговой симплекс-таблицы. Рассматриваемое неравенство приводится к стандартному виду путем добавления остаточной переменной, которая вводится в задачу как базисная: xk + sn+1 = [xk]. Базисная переменная xk из симплекс-таблицы выражает- ся через небазисные переменные и подставляется в последнее выражение, в результате чего получается:
Выполняется очередная итерация двойственного симп- лекс-метода, позволяющая получить целочисленное значение переменной xk. Если полученное решение удовлетворяет условиям цело- численности, то его следует рассматривать как нижнюю (в за- даче максимизации ЦФ) границу задачи. Она характеризуется, таким образом, целочисленностью всех или части переменных и наилучшим в сравнении с другими подзадачами значением ЦФ. Граница вводится для повышения эффективности вычис- лений в том смысле, что, если в результате разрешения оче- редной подзадачи получено худшее, чем граница, решение, дальнейшее ветвление задачи в этом направлении нецелесооб- разно. Тем самым исключаются из рассмотрения те комбина- ции целочисленных значений переменных, которые заведомо будут иметь худшее в сравнении с границей значение ЦФ. Если в результате решения очередной подзадачи будет получено лучшее, чем граница, значение ЦФ, то тогда устанавливается новое значение границы.
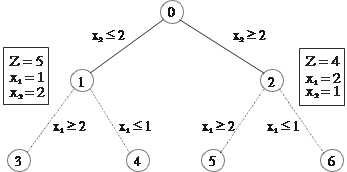
4. Решение подзадачи б). Решение осуществляется анало- гично пункту 3. Пример 9.12. Рассмотрим задачу ЦЛП из примера 9.11. Из табл. 9.12 видно, что обе переменные являются нецелочислен- ными, поэтому на основе одной из них, например x2, органи- зуется ветвящийся процесс поиска целочисленных значений. Дерево подзадач, порождаемых в процессе применения метода ветвей и границ, представлено на рис. 9.5.
Рис. 9.5. Дерево подзадач Исходя из значения выбранной переменной x2 = 1 3/4 фор- мируются две подзадачи: x2 ≤ 2 и x2 ≥ 1. Результат решения вто- рой подзадачи: Z = 4, x1 = 2, x2 = 1. Это решение удовлетворяет требованию целочисленности, поэтому оно может рассматри- ваться в качестве границы. Дальнейшее ветвление задачи не- целесообразно, поскольку оно приведет к худшему решению. Действительно, если продолжить ветвление и рассмотреть подзадачу x1 ≤ 1, то ее решением будет: Z = 3, x1 = 1, x2 = 1. До- пустимого же решения подзадачи x1 ≥ 2 вообще не существует. Первая подзадача имеет решение: Z = 5, x1 = 1, x2 = 2. Как видно, это решение лучше того, что было принято в качестве границы. Поэтому решение второй подзадачи должно быть принято в качестве новой границы задачи. Дальнейшее ветв- ление также нецелесообразно, поскольку приведет к ухудше- нию значения ЦФ. На рис. 9.5 штриховыми линиями показаны те ветви, для которых соответствующие им подзадачи нецеле- сообразны для решения. Таким образом, введением границ удается существенно уменьшить количество решаемых подзадач в ходе поиска оп- тимального целочисленного решения. В настоящее время метод ветвей и границ является наибо- лее надежным средством решения целочисленных задач.
Задачи для самостоятельного решения Используя рассмотренные методы найти решение следу- ющих задач: 9.1. F = 7 x 1 + x 2 → max;
11 x 1 − 3 x 2 − x 4 = 24, 2 x 1 − 7 x 2 − x 5 = 110, x j ≥ 0, x j — целые (j = 9.2. F = − 5 x 1 + 8 x 2 − 3 x 3 + 4 x 4 + 7 x 5 + 6 x 6 → max;
− 4 x 1 − x 2 − 5 x 3 + 3 x 4 + x 5 + 2 x 6 ≤ 60, 0 ≤ x j ≤ 10, x j — целые (j =
x 1 + 1,85 x 2 + x 3 + x 4 ≤ 16, x 1 + x 2 + x 3 + x 4 ≥ 10, 4 x 1 + 6,9 x 2 + 10 x 3 + 13 x 4 ≤ 100, 6,3 x 1 + 5 x 2 + 4 x 3 + 3 x 4 ≤ 100, x j ≥ 0, x j — целые (j = 9.4. F = 5 x 1 + 2 x 2 − 3 x 3 + 2 x 4 + 3 x 5 − 3 x 6 → max;
5 x 1 + 5 x 2 + 7 x 3 + 3 x 5 + 3 x 6 = 10, 2 x 1 + 2 x 2 + 2 x 3 + 3 x 5 = 4, x j ≥ 0, x j — целые (j = Используя метод Гомори для частично-целочисленных за- дач, необходимо определить:
x 1 + 4 x 2 + x 3 = 16, 2 x 1 + 3 x 2 − x 4 = 12, 3 x 1 − 2 x 2 + x 5 = 18, x 1, x 2,…, x 5 ≥ 0.
x 1 + x 2 − x 3 = 5, − x 1 + 3 x 2 + x 4 = 7, 3 x 1 − x 2 + x 5 = 11, x 1, x 2,…, x 5 ≥ 0.
Вопросы для самопроверки 1. В чем состоит смысл постановки и решения задачи ли- нейного программирования?
2. Как осуществляют вербальную и математическую пос- тановку задачи линейного программирования? 3. Дайте характеристику основных методов решения зада- чи линейного программирования. 4. В чем суть геометрического метода решения задачи ли- нейного программирования? 5. В чем состоит алгоритм симплекс-метода решения зада- чи линейного программирования? 6. В чем состоит суть метода искусственного базиса? 7. Дайте определение двойственной задачи линейного про- граммирования. 8. В чем состоит суть решения задачи целочисленного ли- нейного программирования? 9. В чем заключается идея метода Гомори для полностью целочисленных задач линейного программирования? 10. В чем состоит сущность метода ветвей и границ?
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 179; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.19.251 (0.016 с.) |
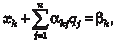
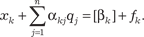


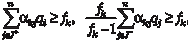
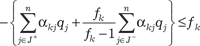
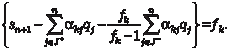
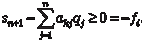

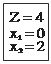

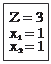
 9 x 1 + 4 x 2 + x 3 = 110,
9 x 1 + 4 x 2 + x 3 = 110,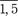 ).
).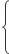 − 2 x 1 − 3 x 2 − 4 x 3 + 2 x 4 + x 5 + x 6 ≤ 24, 3 x 1 + 2 x 2 + 3 x 3 + x 4 + 2 x 5 + x 6 ≤ 30,
− 2 x 1 − 3 x 2 − 4 x 3 + 2 x 4 + x 5 + x 6 ≤ 24, 3 x 1 + 2 x 2 + 3 x 3 + x 4 + 2 x 5 + x 6 ≤ 30,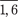 ). 9.3. F = 60 x 1 + 70 x 2 + 120, 4 x 3 + 130 x 4 → max;
). 9.3. F = 60 x 1 + 70 x 2 + 120, 4 x 3 + 130 x 4 → max;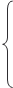 x 1 + x 2 + x 3 + x 4 = 16,
x 1 + x 2 + x 3 + x 4 = 16, ).
).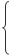 5 x 1 + 6 x 2 + 4 x 3 + 2 x 4 − 3 x 5 + 5 x 6 = 11,
5 x 1 + 6 x 2 + 4 x 3 + 2 x 4 − 3 x 5 + 5 x 6 = 11,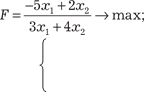 9.5.
9.5.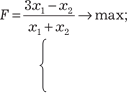 9.6.
9.6.


