Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные уравнения второго порядка, решаемые с помощью понижения порядкаСодержание книги
Поиск на нашем сайте Сущность данного способа состоит в том, что, используя замену переменной, исходное дифференциальное уравнение сводится к дифференциальному уравнению первого порядка. Рассмотрим некоторые типы дифференциальных уравне- ний, которые допускают понижение порядка. 1) y ″ = f (y). Данное дифференциальное уравнение интегрируется с по- мощью подстановки y ′ = p, (6.37) которая приводит исходное дифференциальное уравнение к дифференциальному уравнению с разделяющимися перемен- ными. Получаем
Поэтому имеем . Далее, разделяя переменные, получаем p · dp = f (y) dy. Из полученного уровнения получаем р, а из уравнения 2) y ″ = f (y ′). Данное дифференциальное уравнение с помощью подста- новки y ′ = p (6.37)
, т. е. получаем . 3) y ” = f (x, y ’). Используем подстановку (6.37) и приводим данное диффе- ренциальное уравнение к следующему виду:
Решая данное уравнение, определяем неизвестную функ- цию p. 4) y ” = f (y, y ’)
ренциальное уравнение к виду , где у является ар- гументом. Теперь рассмотрим несколько конкретных примеров. Пример 6.16.
. Это уравнение вида 3. Поэтому используем подстановку y ′ = p и получаем
Полученное дифференциальное уравнение является ли- нейным дифференциальным уравнением первого порядка. Для его решения применим метод Бернулли. p = U · V; p ’ = U ’ · V + V ’ · U.
;
В качестве функции V примем какое-то конкретное диф- ференциального уравнения: V ′ − 2/ x · V = 0 Тогда функцию U найдем из дифференциального урав- нения U ′ · V = 2 x 3;
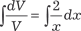 . .
Интегрируя, получаем ln| V | = 2ln| х |, или V = x 2. Зная функцию V, ищем функцию U.
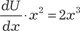 , или . , или .
Из последнего выражения находим
Последнее выражение и есть общее решение исходного дифференциального уравнения. Пример 6.17. Найти общее решение дифференциального уравнения 1 + (y ′)2 − 2 y · y ″ = 0.
.
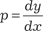 получаем получаем  , или , или
.
Это выражение и есть общее решение исходного диффи- ринциального уравнения. Пример 6.18. Найти частное решение диффиринциального уравнения y ″ = y ′ · ln y ′, если заданы начальные условия
;
Имея в виду, что , получим Тогда получаем
Интеграл, стоящий в правой части последнего выражения, является “неберущимся”, т. е. он не выражается в элементар- ных функциях. Для его решения надо использовать численные методы, например разложить в ряд подынтегральную функ- цию ez. Мы же воспользуемся тем, что надо найти не общее, а част- ное решение исходного дифференциального уравнения. Опре- делим это частное решение без нахождения общего, используя заданные начальные условия.
. Поэтому имеем y ′ = 1 или y = x + C 4. Для нахождения постоянной С4 используем начальное ус- ловие Поэтому получаем частное решение y = x, удолетворяю- щее заданным начальным условиям. Пример 6.19.
. Это уравнение вида 1, поэтому применяем замену у ′ = р и получаем Разделяем переменные и имеем
.
Учитывая, что
,
Последнее выражение и есть общее решение исходного дифференциального уравнения.
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 168; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.007 с.) |

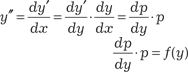 .
.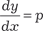 находим общий интеграл исходного дифференциального уравнения f (x, y, C 1, C 2) = 0.
находим общий интеграл исходного дифференциального уравнения f (x, y, C 1, C 2) = 0. приводится к дифференциальному уравнению с разделяющи- мися переменными:
приводится к дифференциальному уравнению с разделяющи- мися переменными: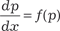 , а далее, разделяя переменные,
, а далее, разделяя переменные, .
.
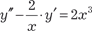
 .
.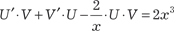
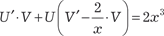


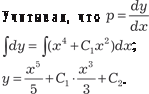 , находим
, находим  ;
;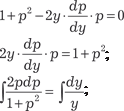 Это дифференциальное уравнение вида 4. Поэтому, ис- пользуя подстановку y ′ = p, получаем
Это дифференциальное уравнение вида 4. Поэтому, ис- пользуя подстановку y ′ = p, получаем .
.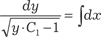
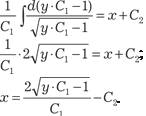 ;
; ;
;  .
. Это уравнение 2. Поэтому используем подстановку y ′ = p. Исходное дифференциальное уравнение запишется в виде
Это уравнение 2. Поэтому используем подстановку y ′ = p. Исходное дифференциальное уравнение запишется в виде ;
; 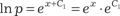 ;
; .
.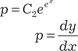 Так как постоянная может быть любой, обозначим
Так как постоянная может быть любой, обозначим  и тогда получаем.
и тогда получаем. . Делаем под- становку e x = z, x = ln z, dx = dz / z.
. Делаем под- становку e x = z, x = ln z, dx = dz / z.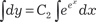 .
. .
. Используем начальное условие к уравнению
Используем начальное условие к уравнению . Обозначим
. Обозначим  и получим .
и получим .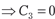
 и получаем C 4 = 0.
и получаем C 4 = 0.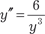
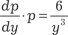 .
.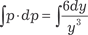 ;
;
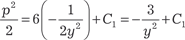 ;
;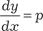 , имеем . Разделяя пе- ременные, получаем.
, имеем . Разделяя пе- ременные, получаем.