
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Признаки сходимости положительных числовых рядовСодержание книги
Поиск на нашем сайте Признаки сравнения Если все члены рядов u 1 + u 2 + … + u n + … (7.2) v 1 + v 2 + … + v n + … (7.3) неотрицательны и u n v n, n = 1, 2, 3, …, то из сходимости ряда (7.3) следует сходимость ряда (7.2). Из расходимости ряда (7.2) следует расходимость ряда (7.3). Если все члены рядов (7.2) и (7.3) положительны и сущест- вует Пример 7.5. Ряд Пример 7.6. Ряд Признак Коши Если все члены ряда w 1 + w 2 + … + w n + … неотрицательны и существует Пример 7.7. Исследуем сходимость ряда
Применяем к данному ряду признак Коши
и видим, что он сходится. Признак Даламбера Если все члены ряда w 1 + w 2 + … + w n + … положительны и существует
Пример 7.8. Исследуем сходимость ряда Применяем к данному ряду признак Даламбера
и видим, что он сходится. Интегральный признак сходимости Коши
. Пример 7.9. Исследуем сходимость ряда
т. е. ряд сходится. Абсолютная и условная сходимость рядов Числовой ряд w 1 + w 2 + … + w n + … (7.4) называется абсолютно сходящимся, если сходится ряд, состав- ленный из абсолютных величин его членов: | w 1| + | w 2| + … + | w n | + … (7.5) Абсолютно сходящийся ряд всегда сходится. Если ряд (7.4) сходится, а ряд (7.5) расходится, то говорят, что ряд (7.4) схо- дится условно. Теперь приведем теорему Лейбница, которая применяется для знакочередующихся рядов; т. е. рядов, у которых положитель- ные и отрицательные члены следуют друг за другом поочередно. Теорема 7.2. Ряд w 1 - w 2 + w 3 - w 4 + … + (-1) n -1 w n + …, где все w n > 0, сходится, если все его члены таковы, что w 1 > w 2 > > w 3 > … > w n > … и превосходит первого члена. Свойства абсолютно и условно сходящихся рядов 1. Если ряд сходится абсолютно, то новый ряд, полученный из него перестановкой членов, также сходится и имеет ту же сумму, что и исходный ряд. 2. Если ряд сходится условно, то какое бы число S ни взять, можно так переставить члены в этом ряде, чтобы сумма преоб- разованного ряда была равна именно S. 3. Если ряд сходится условно, то можно так переставить члены в этом ряде, что новый ряд будет расходиться. Функциональные ряды
(7.6)
где W 1(x), W 2(x), …, W n (x), … — некоторые функции, определен- ные на одном и том же множестве D, называется функциональ- ным рядом. Множество E D всех значений x, при которых функцио- нальный ряд (7.6) сходится (как числовой ряд), называется об- ластью сходимости этого ряда. Функция S (x), x E является суммой ряда (7.6), если
где S n (x) = W 1(x) + W 2(x) + … + W n (x). Если функция S (x), x P (P E) является суммой ряда (7.6), то говорят, что этот ряд сходится на множестве Р к функ- ции S (x). Функциональный ряд называется равномерно сходящим- ся на множестве P к функции S (x), если для числа > 0 су- ществует такой номер N, что при n N сразу для всех x P выполняется неравенство | S (x) - S n (x)| <. Если функциональный ряд сходится на множестве P, то на этом множестве сходимость не обязана быть равномерной, но на некотором подмножестве множества P сходимость может оказаться равномерной. Приведем признак равномерной сходимости Вейерштрас- са. Если члены функционального ряда W 1(x) + W 2(x) + … + W n (x) + … удовлетворяют на множестве P неравенствам | W n (x)| W n (n = 1, 2, 3, …), где W n — члены сходящегося числового ряда W 1 + W 2 + … + W n + …, то функциональный ряд сходится на множестве P равномерно.
Ряд сходится на P = (-; +) равномерно, так как всегда и ряд Если функции W n (x) непрерывны на [ a, b ], а составленный из них ряд W 1(x) + W 2(x) + … + W n (x) + … сходится равномерно на этом отрезке к функции S (x), то: 1) функция S (x) на [ a, b ] непрерывна; 2) Пример 7.11.
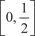 сходится рав- номерно к функции, поэтому сходится рав- номерно к функции, поэтому
или Если функции W n (x) имеют непрерывные производные на отрезке [ a, b ] и на этом отрезке: 1) ряд W 1(x) + W 2(x) + … + W n (x) + … сходится к функции S (x); 2) ряд W 1 (x) + W 2 (x) + … + W n (x) + … сходится равномерно, то S (x) имеет на [ a, b ] непрерывную про- изводную и S (x) = W 1 (x) + W 2 (x) + … + W n (x) + …. Степенные ряды
Функциональный ряд.
где a n (n = 0, 1, 2, …) и x 0 — некоторые числа, называют степен- ным рядом с центром в точке x 0. Возможны следующие три случая: 1) степенной ряд (7.7) сходится только при x = x 0 (везде расходящийся ряд); 2) степенной ряд (7.7) сходится (причем абсолютно) при любых значениях (всюду сходящийся ряд); 3) существует число R > 0 такое, что ряд (7.7) сходится аб- солютно при | x - x 0| < R и расходится при | x - x 0| > R (радиус сходимости ряда). R = 0 для всюду расходящегося ряда и R = для всюду сходящегося ряда. Интервал (x 0 - R, x 0 + R) называют интервалом сходимости степенного ряда (7.7). При этом на концах интервала сходимос- ти степенной ряд может как сходиться, так и расходиться. Пример 7.12.
Найдем область сходимости степенного ряда Положим
следовательно, данный степенной ряд сходится абсолютно при | x | < 2 и расходится при | x | > 2, а радиус его сходимости равен 2 (R = 2). Исследуем сходимость ряда на концах интервала сходи- мости: при x = 2 ряд ряд
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 188; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.006 с.) |

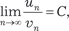 0 < C < +, то эти ряды сходятся или расходят- ся одновременно.
0 < C < +, то эти ряды сходятся или расходят- ся одновременно. расходится, так как гармонический ряд
расходится, так как гармонический ряд  расходится и
расходится и 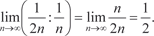
 расходится, так как его члены (начиная со второго) больше соответствующих членов гармони- ческого ряда
расходится, так как его члены (начиная со второго) больше соответствующих членов гармони- ческого ряда 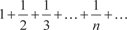 , который расходится.
, который расходится. , то при b < 1 этот ряд сходится, а при b > 1 расходится (при b = 1 данный признак не дает возможнос- ти судить о поведении ряда).
, то при b < 1 этот ряд сходится, а при b > 1 расходится (при b = 1 данный признак не дает возможнос- ти судить о поведении ряда).
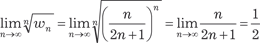
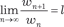 , то при l < 1 этот ряд сходится, а при l > 1 этот ряд расходится (при l = 1 данный признак не дает возмож- ности судить о поведении ряда).
, то при l < 1 этот ряд сходится, а при l > 1 этот ряд расходится (при l = 1 данный признак не дает возмож- ности судить о поведении ряда).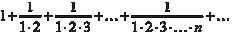
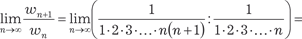
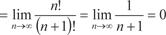
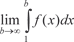
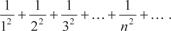

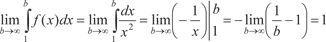
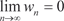 , а его сумма положительна и не
, а его сумма положительна и не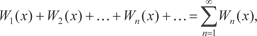
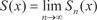
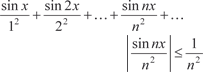 Пример 7.10.
Пример 7.10.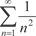 сходится.
сходится.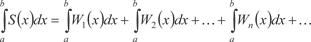
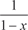
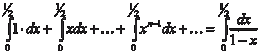
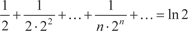 .
.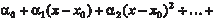
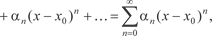 (7.7)
(7.7)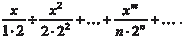
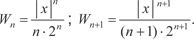 Тогда по признаку Даламбера имеем
Тогда по признаку Даламбера имеем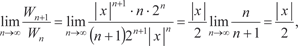
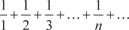 расходится, а при x = -2
расходится, а при x = -2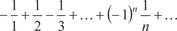 сходится. Поэтому область схо- димости исходного степенного ряда E = [-2; 2).
сходится. Поэтому область схо- димости исходного степенного ряда E = [-2; 2).


