Дифференциальные уравнения первого порядка с разделяющимися переменными

В общем случае такие уравнения имеют вид: f 1(x) f 2(y) dx +

+ f 3(x) f 4(y) dy = 0.

Разделим обе части этого дифференциального уравнения на произведение f 2(y) f 3(x), предполагая, что оно не равно нулю.

Далее получаем

 

 

В полученном дифференциальном уравнении при dx сто- ят только функции от х, а при dy — только функции от у, т. е. переменные разделены. Интегрируем левую и правую части последнего равенства и получаем:

Это и есть общий интеграл исходного дифференциального уравнения.

Рассмотрим несколько конкретных задач.

Пример 6.1. Найдем частное решение дифференциально- го уравнения. xdx + ydy = 0, если начальное условие таково y | x =2 = 10.

1.

ydy = − xdx,                                           у ² + х ² = 2 С

Так как постоянная может быть любой, то примем 2 С 1 = С.

2

Тогда получим общее решение исходного дифференциального уравнения у ² + х ² = С ².

С геометрической точки зрения это решение представляет собой семейство концентрических окружностей с центром в на- чале координат и радиусом С (см. рисунок).

 

Найдем теперь частное решение для заданных начальных условий, т. е. выделим из семейства окружностей одну. Полу- чим 10² + 2² = С ² => С ² = 104,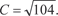

Поэтому частное решение имеет вид: у ² + х ² = 104.

Пример 6.2. Найдем общее решение дифференциального уравнения:

1 + y ′ + y + xy ′ = 0.

Перепишем его в виде:

;

.

Правую и левую часть домножим на dx.

(1 + y) dx + dy (1 + x) = 0.

Правую и левую части делим на (1 + х) ≠ 0:

Правую и левую части делим на (1 + y) ≠ 0:

;

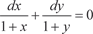Теперь интегрируем правую и левую части:

 

 

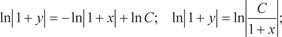
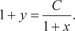
Окончательно получаем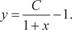

Полученное выражение и есть общее решение исходного дифференциального уравнения.

Пример 6.3. Найдем общее решение дифференциального уравнения

2 xyy ′ = y ² − 1.

Перепишем его в виде

Домножим правую и левую часть на dx:

2 xydy = (y ² − 1) dx.

Разделим правую и левую части на х ≠ 0:

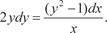
Разделим правую и левую части на у ² − 1 ≠ 0:

Теперь проинтегрируем правую и левую части полученно- го выражения

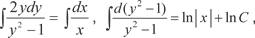
ln | y ² − 1| = ln | xC |, y ² − 1 = xC,

Полученное уравнение и есть общее решение исходного дифференциального уравнения.

Пример 6.4. Найти частое решение дифференциального уравнения (x ² + 4) y ′ − 2 xy = 0, если задано следующее началь- ное условие y | x =1 = 5.

Перепишем исходное дифференциальное уравнение так:

Домножим правую и левую части на dx:

(x ² + 4) dy − 2 xydx = 0.

Разделим правую и левую части на х ² + 4:

Разделим правую и левую части на у ≠ 0:

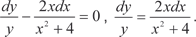
Теперь интегрируем обе части полученного выражения.

ln| y | = ln| x ² + 4| + ln C, ln| y | = ln| C (x ² + 4)|.

y = C (x ² + 4).

Полученное уравнение и есть общее решение исходного дифференциального уравнения. Геометрически оно представ- ляет собой семейство парабол.

По заданным начальным условиям найдем частое решение, т. е. выделим конкретную параболу из полученного семейства.

5 = С (1²+4) => 5 = 5 С => С = 1.

Поэтому частное решение имеет вид у = х ² + 4. Рассмотрим некоторые классы дифференциальных урав-

нений, которые сводятся к дифференциальным уравнениям с разделяющимися переменными.