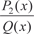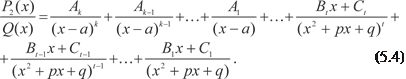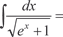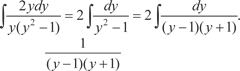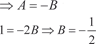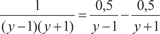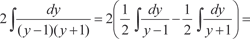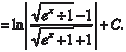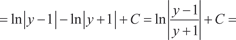Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Бывает случаи, когда формулу (5. 2) надо применять несколько раз.
Пример 5.7. чим [К интегралу опять применим формулу (5.2), полу-
Переносим в левую часть и получаем
3. Метод замены переменной. Его применяют в том слу- чае, если исходный интеграл сложно или невозможно с помо- щью алгебраических и иных преобразований свести к одному или нескольким табличным интегралам. Способ заключается в следующем: заменяется новой пе- ременной такая часть подынтегральной функции, при диффе- ренцировании которой получается оставшаяся часть подын- тегрального выражения (не считая постоянного множителя, на который всегда можно умножить или разделить подынтег- ральное выражение). Метод замены переменной основан на следующей теореме. Пусть некоторая функция (t) = x определена и дифференци- руема на некотором промежутке [ a, b ], пусть X — множество значений этой функции, на котором определена функция f (x). Тогда, если на множестве Х функция f (x) имеет первообраз- ную, то на отрезке [a, b] справедлива формула
В некоторых случаях лучше использовать замену пере- менной не в виде x = (t), а t = (x). Приведем конкретные примеры. Пример 5.9.
лаем замену переменной: поэтому полу- чим]
[Теперь делаем замену переменной
[Возвращаем переменную х и получаем]
=[Теперь делаем замену переменной
[Возвращаем переменную х и получаем]
[Заметим, что
[Заметим, что
[Теперь делаем замену переменной [Возвращаем переменную х ]
[Заметим, что
Интегрирование рациональных дробей Любая рациональная функция R (x) может быть представле- на в виде дроби, т. е. Если степень числителя (m) больше или равна степени знаменателя (n), то, разделив P (x) на Q (x), получим многочлен P 1(x) и в остатке многочлен P 2(x) не выше (n − 1) степени, т. е.
двух видов
Каждому множителю (x 2 + px + q) t соответствует сумма t простейших дробей вида:
 Имеет место следующее разложение дроби на слага- емые: Имеет место следующее разложение дроби на слага- емые:
Пример 5.15.
[Делаем замену переменной, обозначив  тогда получим тогда получим
где А и В неизвестные коэффициенты, которые необходимо найти. Освобождаясь от знаменателя, имеем: 1 = A (y + 1) + B (y − 1); 1 = Ay + A + By − B. Приравнивая коэффициенты при y и y 0, получим систему уравнений для определения А и В.
Тогда получим:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 88; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.252.199 (0.011 с.) |
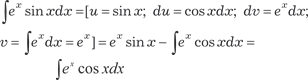 u = cos x; du = -sin xdx; dv = exdx; v = ex ]
u = cos x; du = -sin xdx; dv = exdx; v = ex ]



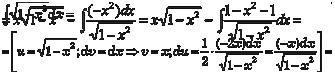
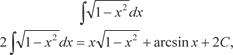 Пример 5.8.
Пример 5.8.
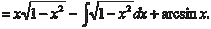
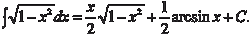

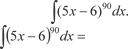 Найти
Найти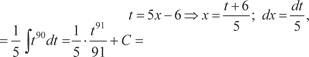 [Можно разложить подынтегральную функцию, используя бином Ньютона, но это будет слишком длинно, поэтому де-
[Можно разложить подынтегральную функцию, используя бином Ньютона, но это будет слишком длинно, поэтому де-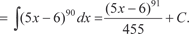

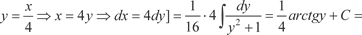

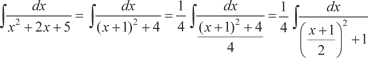


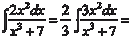



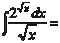
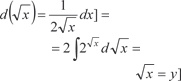 Пример 5.13.
Пример 5.13.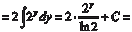
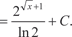
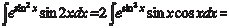
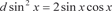 ]
]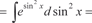

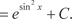
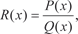 где P (x) и Q (x) — многочлены.
где P (x) и Q (x) — многочлены. Интегрирование P 1(x) проходит без проблем. Надо проинтегрировать правильную рациональную дробь, степень числителя которой меньше степени знаменателя
Интегрирование P 1(x) проходит без проблем. Надо проинтегрировать правильную рациональную дробь, степень числителя которой меньше степени знаменателя  .
.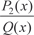 можно представить в виде суммы простейших дробей
можно представить в виде суммы простейших дробей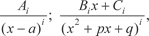 где A i, B i, C i — постоянные.
где A i, B i, C i — постоянные.