Интегрирование тригонометрических функций
Интеграл вида 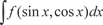 с помощью подставки с помощью подставки  можно преобразовать в интеграл от рациональной функции. можно преобразовать в интеграл от рациональной функции.
Используются следующие тригонометрические формулы:
Из равенства x = 2arctg u имеем 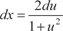 . В результате ука- занной подстановке исходный интеграл преобразуется к виду . В результате ука- занной подстановке исходный интеграл преобразуется к виду

т. е. подынтегральная функция рациональна относительно u.
Пример 5.16.
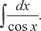
Применим подстановку  и получаем: и получаем:
[Воспользуемся формулой 16 из таблицы интегралов.]
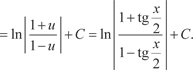
С помощью указанной подстановки хорошо “берутся” ин- тегралы вида 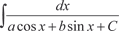 . .
Интегрирование функций 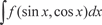 с помощью под- становки с помощью под- становки  всегда приводит к успеху, но в силу своей об- щности она не всегда является оптимальной. всегда приводит к успеху, но в силу своей об- щности она не всегда является оптимальной.
Интегралы вида  находятся следующим образом: находятся следующим образом:
а) если m — целое положительное нечетное число, то при- меняется подстановка cos х = U.
Пример 5.17.
 [делаем подстановку cos x = U ] = [делаем подстановку cos x = U ] =
b) если n − целое положительное нечетное число, то приме- няется подстановка sin x = U.
Пример 5.18.
[делаем замену переменной sin x = U ] =
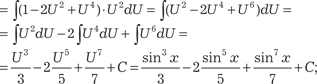
с) если (n + m) − четное отрицательное число, то применя- ется подстановка tg x = U:
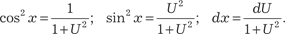
Пример 5.19.
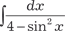 = [делаем замену tg x = U ] = [делаем замену tg x = U ] 
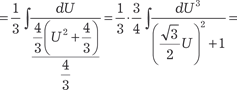
[делаем замену  ; ; 
;
d)
если m и n − целые неотрицательные четные числа, то используются формулы
Пример 5.20.

Интегралы от иррациональных функций
а) Рассмотрим интеграл  , где R — ра- циональная функция своих аргументов, т. е. над величинами х, хm/n, …, хk/t проводятся только рациональные операции. , где R — ра- циональная функция своих аргументов, т. е. над величинами х, хm/n, …, хk/t проводятся только рациональные операции.
Пусть р — общий знаменатель дробей  . .
Теперь делаем подстановку х = у р; dx = ру р −1 dy. Тогда каж- дая дробная степень х выразится через целую степень, т. е. по- дынтегральная функция преобразуется в рациональную фун- кцию от у.
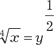 Пример 5.21. Пример 5.21.
Так как общий знаменатель дробей и  это 4, то делаем замену х = у 4, dx = 4 у 3 dу, это 4, то делаем замену х = у 4, dx = 4 у 3 dу, 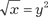 ;. ;.
В результате получаем 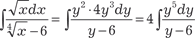 . .
 Делим числитель на знаменатель и получаем Делим числитель на знаменатель и получаем
у 5 y − 6
 − у 5 − 6 у 4 у 4 + 6 у 3 + 36 у 2 + 216 у + 1296 − у 5 − 6 у 4 у 4 + 6 у 3 + 36 у 2 + 216 у + 1296
6 у 4
 − 6 у 4 − 36 у 3 − 6 у 4 − 36 у 3
36 у 3
 − 36 у 3 − 216 у 2 − 36 у 3 − 216 у 2
216 у 2
 − 216 у 2 − 1296 у − 216 у 2 − 1296 у
1296 у
− 1296 у − 7776
7776
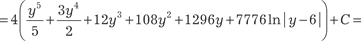
.
б) Теперь рассмотрим интеграл вида
Он сводится к интегралу от рациональной функции под- становкой
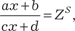
где S — общий знаменатель дробей .
Пример 5.22.
В данном примере 
Так как общий знаменатель дробей и 2 равен 2, то полу- чаем х + 1 = Z 2.
Поэтому dх = 2 ZdZ и исходный интеграл примет вид

Разлагаем подынтегральную функцию на элементарные дроби и получаем:
Отбрасываем знаменатель и имеем:
Z + 4 = А (Z 2 + Z + 1) + (Z − 1) (В Z + С);
Z + 4 = А Z 2 + А Z + А + В Z 2 + С Z − В Z − С;

Решая полученную систему, находим искомые коэффици- енты А, В, С.
Складываем второе и третье уравнения полученной систе- мы и получаем
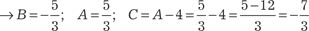 . .
Поэтому получаем
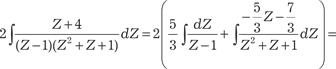
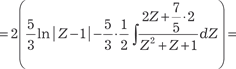
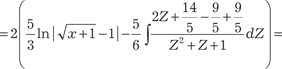


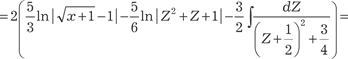
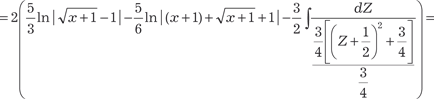

=[делаем замену переменной ; ]
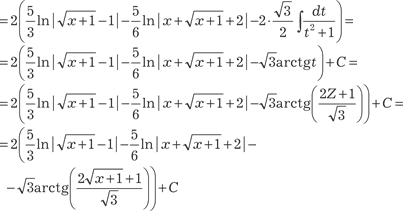
|