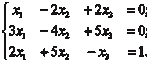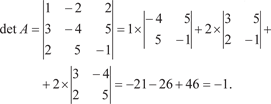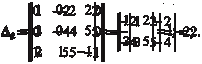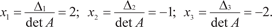Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы линейных алгебраических уравненийСодержание книги
Поиск на нашем сайте
Рассмотрим системы линейных алгебраических уравне- ний (СЛАУ).
(2.1)
a ij — коэффициенты; x 1, x 2, …, x n — неизвестные; b 1, b 2, …, b m — свободные члены. Систему (2.1) можно записать в матричном виде:
где — матрица системы;
— вектор свободных членов;
—
Решением СЛАУ называется любая совокупность n чисел (x 1, x 2, …, x n), которая обращает каждое уравнение системы (2.1) в верное равенство. Любая СЛАУ вида (2.1) может иметь одно решение, беско- нечное множество решений, ни одного решения. Если СЛАУ имеет хотя бы одно решение, то она называет- ся совместной. Если СЛАУ не имеет решений, то она — несов- местная. Если все свободные члены СЛАУ (2.1) равны нулю, то сис- тема называется однородной, а если хотя бы один из свободных членов системы не равен нулю, то она называется неоднород- ной. Система однородных уравнений всегда совместна, т. е. она имеет хотя бы одно решение (х j =0). Перед решением СЛАУ надо убедиться в ее совместности. Поэтому приведем без доказательства теорему Кронекера-Ка- пелли, которая позволяет это сделать. Дополним матрицу А системы (2.2) столбцом свободных чле- нов. В результате этого получим матрицу порядка m (n + 1), которую называют расширенной матрицей системы (С):
Через r (А) и r (С) обозначим ранги матриц А и С соответс- твенно. Теперь сформулируем теорему. Теорема 2.3 (Кронекера-Капелли). Для того чтобы СЛАУ вида (2.2) была совместна, необходимо и достаточно, чтобы ранг матрицы системы (r (А)) был равен рангу расширенной матри- цы системы (r (С)), т. е. r (А) = r (С). Здесь возможны два случая: 1) если r (А) = r (С) = = n, где n — число неизвестных в систе- ме (2.2), то СЛАУ имеет единственное решение; 2) если r (А) = = r (С) < n, то СЛАУ имеет бесконечное множество решений. СЛАУ можно решать или прямыми или итерационными методами. В прямых (точных) методах решение системы (2.2) нахо- дится за конечное число арифметических действий. К прямым методам относятся метод Гаусса и его модификации, метод квадратного корня, метод Крамера и др.
Итерационные методы (методы последовательных при- ближений) состоят в том, что решение системы (2.2) находится как lim (предел) при k → последовательных приближений х ( k ), где k — номер итерации. Обычно за конечное число итераций этот предел не достигается. Как правило, задается некоторое малое число > 0 (точность) и вычисления проводятся до тех пор, пока не будет выполнено условие
К итерационным методам относятся: метод Якоби, метод Зейделя, метод релаксации, метод минимальных невязок, ме- тод скорейшего спуска и др. В предлагаемом учебнике рассмотрим прямые методы: ме- тод Гаусса и метод Крамера. Рассмотрим метод Гаусса решения СЛАУ. Он состоит из двух шагов. На первом шаге мы приводим исходную систему уравнений к верхнему треугольному виду, а на втором шаге на- ходим неизвестные (х j), начиная с последнего.
(2.3)
Исключаем неизвестное x 1 из всех уравнений, начиная со второго. Для этого из второго уравнения почленно вычтем пер- вое, умноженное на a 21/ a 11, из третьего почленно вычтем пер-
(2.4)
где
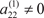 , если он равен нулю, то переставляем уравнение места- ми, т. е. из третьего уравнения системы (2.4) вычитаем второе, умноженное на коэффициент , если он равен нулю, то переставляем уравнение места- ми, т. е. из третьего уравнения системы (2.4) вычитаем второе, умноженное на коэффициент 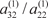 , из четвертого уравнения системы (2.4) вычитаем второе, умноженное на коэффициент , из четвертого уравнения системы (2.4) вычитаем второе, умноженное на коэффициент 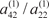 и т. д. В результате мы получаем следующую систему уравнений: и т. д. В результате мы получаем следующую систему уравнений:
(2.5)
где Аналогичный процесс мы продолжаем далее и на (n -1)- м шаге приходим к следующей системе уравнений.
То есть исходную систему уравнений (2.3) привели к верх- нему треугольному виду (первый шаг метода Гаусса завершен). Второй шаг (обратный ход) заключается в решении системы уравнений (2.6). Он осуществляется следующим образом: из последнего уравнения системы (2.6) находим
(2.6) находим x n −2 и т. д. до x 1. Алгоритм Гаусса состоит из однотипных операций, кото- рые легко программируются. Решим систему уравнений, используя метод Гаусса. Пример 2.6.
(2.8)
Теперь исключим из третьего уравнения системы (2.8) не- известное x 2. Для этого умножим поэлементно второе уравне- ние системы (2.8) на (−3) и вычтем из третьего уравнения сис- темы (2.8).
(2.9)
Из системы уравнений (2.9) последовательно находим не- известные х, начиная с последнего (x 3), т. е. x 3 = −1;
Теперь рассмотрим метод Крамера решение СЛАУ. Рассмотрим систему уравнений (2.3), которую запишем в матричном виде
где — матрица системы;
—
—
Если определитель матрицы А (det А) не равен нулю, то су- ществует A −1. Домножим слева систему (2.10) на A −1, получим A − 1 AX = A − 1 B, так как A − 1 A = E, то имеем EX = A −1 B, а так как EX = X, то
(2.12)
(2.13)
Числители равенств (2.13) есть разложения по элементам 1, 2, …, n -го столбцов определителя, полученного из det А заме- ной в нем 1, 2, …, n столбцов столбцом свободных членов, т. е.
Таким образом, неизвестные xi можно найти по формуле
где i = 1, 2, …, n. Решим систему уравнений, используя метод Крамера.
Вначале найдем определитель исходной системы
Затем находим
и определяем неизвестные x i; i = 1, 2, 3:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 111; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.9.175 (0.012 с.) |

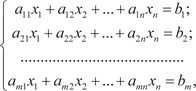
 где
где AX = B, (2.2)
AX = B, (2.2)
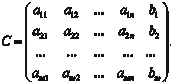
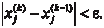
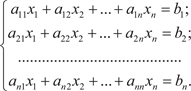
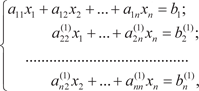
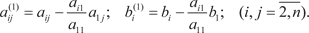
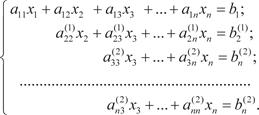
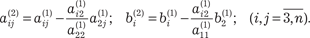
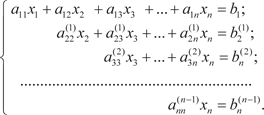
 , исполь- зуя найденное значение x n из предпоследнего (n−1) уравнения системы (2.6) находим x n −1, затем из (n −2) уравнение системы
, исполь- зуя найденное значение x n из предпоследнего (n−1) уравнения системы (2.6) находим x n −1, затем из (n −2) уравнение системы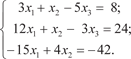
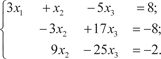
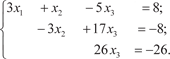
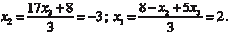
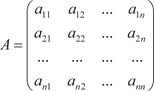
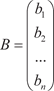
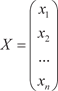
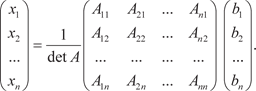
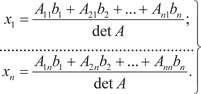
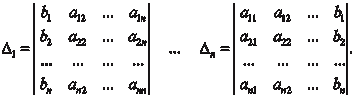
 (2.14)
(2.14)