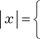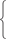Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Некоторые сведения о функцияхСодержание книги
Поиск на нашем сайте
В любой области науки мы встречаемся с различными ве- личинами. Под величиной понимают все то, что может быть из- мерено и (или) вычислено и выражено числом или числами. В естественных, технических и гуманитарных науках имеют дело с различными величинами, например, скоростью, силой, температурой, себестоимостью, валовым внутренним продуктом какой-либо страны, количеством преступлений в каком-то регионе и др. А в математике конкретные величины не участвуют, т. е. рассматривают величины вообще, не принимая во вниманиe их физический смысл. Все величины можно разделить на переменные и посто- янные. Переменной называется такая величина, которая прини- мает различные числовые значения. Величина, которая не ме- няет свое числовое значение, называется постоянной. Все процессы характеризуются взаимоизменяемостью не- скольких переменных величин, а это приводит к важнейшему понятию математики функциональной зависимости. Часто одни и те же величины могут в одних случаях быть переменными, а в других постоянными. Например, в формуле F = ma величины m (масса) и a (уско- рение) могут быть как постоянными, так и переменными. Но существуют и фундаментальные постоянные, которые сохраняют свое значение, по крайней мере, в нашей Mетага- лактике.
 ве- личина — фундаментальная постоянная. ве- личина — фундаментальная постоянная.
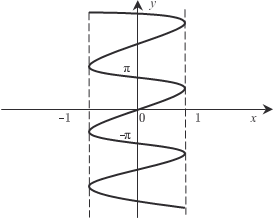
Установление и описание связей между величинами одна из основных задач математического анализа, который включа- ет в себя ряд дисциплин: теорию пределов, дифференциальное и интегральное исчисления, теорию рядов и др. Некоторые све- дения из этих дисциплин мы рассмотрим в главах 3−7. Теперь приведем определение функции одного независи- мого аргумента. Переменная величина y называется функцией переменной величины x на множестве определения D, если каждому значе- нию x D по какому-то закону поставлено в соответствие одно (несколько, бесконечно много) значение (значений) y. В первом случае функция называется однозначной, напри- мер, y = x + 1 (рис. 3.1).
Рис. 3.1 А во втором случае — многозначной, например, y = Arcsin x (рис. 3.2). Величину x из области D можно брать произвольно, поэ- тому она называется аргументом или независимой переменной. А величина y будет зависеть от выбранной величины x, поэто- му ее называют зависимой переменной или функцией.
Область D может быть любой, но, как правило, использу- ются области двух видов: • множество целых неотрицательных чисел или какие-то части этого множества;
Рис. 3.2 • один или несколько интервалов (конечных или бесконеч- ных) числовой оси. В первом случае имеем функцию целочисленного аргумен- та, а во втором — непрерывного. Тот факт, что величина y есть функция аргумента x, обыч- но записывают так: y = f (x). Множество всех значений функции y обозначим через E. Функцию можно задать с помощью таблицы, в виде гра- фика (преимуществом этого способа является его наглядность) или аналитически (формулой). Последний способ является са- мым распространенным. Все функции можно разделить на два класса: элементар- ные и неэлементарные. К элементарным функциям относятся основные элемен- тарные функции: y = xn (n R), y = ax (a > 0, a 1); y = log a x (a > 0, a 1), y = sin x, y = cos x; y = tg x, y = ctg x, y = sec x, y = cosec x; y = arcsin x, y = arccos x, y = arctg x, y = arcctg x и функции, полученные из основных элементарных функций при помощи конечного числа арифметических действий и ко- нечного числа операций взятия функции от функции и задан- ные одной формулой [44].
и т. д. Все функции, не подходящие под данное определение, эле- ментарными функциями не являются. Например, функция
0 при x = 0; 1 при x > 0 не является элементарной функцией, так как задана тремя формулами. А функция f (n) = 1 · 2 · 3 · … n = n! не будет элементарной, так как количество операций умножения, которое нужно со- вершить для получения f (n), не будет являться конечным. Элементарные функции подразделяют на два класса: ал- гебраические и трансцендентные функции. Функция называется алгебраической, если ее значения можно получить, произведя над аргументом конечное число алгебраических действий: вычитаний, сложений, умножений, делений, возведений в степень с рациональным показателем. Функция, которая не является алгебраической, называет- ся трансцендентной.
; .
Трансцендентнымиявляются, например, следующиефунк-
ции: y = cos2 x, y = ex, Алгебраические функции можно разделить на рациональ- ные и иррациональные. Алгебраическая функция называется рациональной, если среди действий, которые проводятся над аргументом, отсутствует извлечение корней. Алгебраическая функция, которая не является рациональной, называется ир- рациональной. Например, к рациональным функциям относятся:
Функции
т. е. значение f (- x) = f (x). График четной функции симметричен отно- сительно оси ординат (рис. 3.3). Четными функциями являются, например, y = cos x, y = x 2. Функция y = f (x) называется нечетной, если при изменении зна- ка y любого значения аргумента из Рис. 3.3 ее области определения меняется только знак значения фун- кци и, а модуль этого значения не меняется, т. е. f (- x) = - f (x). График нечетной функции симметричен относительно начала координат (рис. 3.4). Нечетными функциями являются, например, y = sin x, y = x 3. Функция можент быть ни четной, ни нечетной. Например, таковыми будут функции: y = x − 3; y = 5 x.
Рис. 3.4 Функция y = f (x) называется пе- риодической, если существует такое число Т > 0, что для ∀ x справедливо равенство
Если функция является пери- одической, то выполняются следу- ющие равенства: f (x + 2 T) = f (x); f (x + 3 T) = f (x); f (x − T) = f (x); f (x − 2 T) = f (x) и вообще f (x + + kT) = f (x) при ∀ x, k ∈ Z (Z − множество целых чисел). Наименьшее положительное число Т, при котором со- блюдается условие (3.1), называется периодом функции. Пери- одической функцией является, например, функция y = cos x, y которой Т = 2π. Если периодическая функция не определена в точке x 0, то она не определена и во всех точках x 0 + kT. Напри- мер, функция y = ctg x, y которой Т = π, не определена в точках πk. Интервал аргумента, в котором функция возрастает, назы- вается интервалом возрастания функции, а интервал, в кото-
Рис. 3.5 растает (рис. 3.5). Значение функции, большее или меньшее всех других ее значений на некотором интервале, называется соответственно наибольшим или наименьшим значением функции на этом ин- тервале. Например, функция у = х 2 имеет наименьшее значе- ние у = 0 на интервале (-∞; +∞). Рассмотрим области определения и графики некоторых основных элементарных функций. Степенная функция у = хn определена на интервале х ∈ (-∞; +∞), если n ∈ Z + (целые по- ложительные числа). Приведем графики функций у = х 4 (рис. 3.6); у = х 3 (рис. 3.7):
Рис. 3.6 Рис. 3.7
Приведем графики функций (рис. 3.8) и
Рис. 3.8 Рис. 3.9 Показательная функция у = ах определена при всех зна- чениях х. Приведем графики функций у = 2 х и у = (1/2) х (рис. 3.10) Логарифмическая функция у = log a x определена только для х > 0 (рис. 3.11).
Тригонометрические функции:
Рис. 3.10 Рис. 3.11
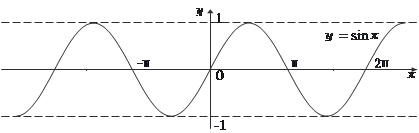
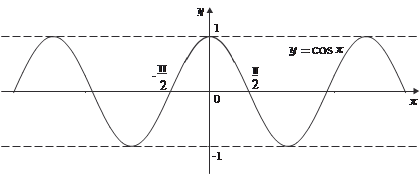
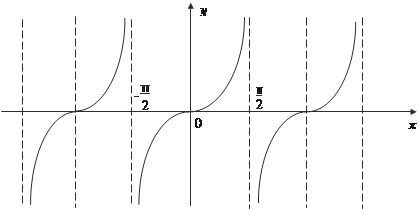
Функции у = sin x (рис. 3.12) и y = cos x (рис. 3.13) определе- ны при всех значениях х. Рис. 3.12 Функция у = tg x определена при всех значениях х, кроме точек π/2 + π k, k ∈ Z (график на рис. 3.14). Функция у = cosec x = 1/sin x определена при ∀ х, кроме х = π k, k ∈ Z. Приведем график этой функции (рис. 3.15).
Рис. 3.13
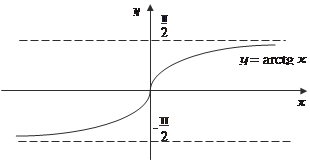
Рис. 3.14 Функция у = arccos х, определена на отрезке -1 ≤ х ≤ 1, а значения функции заполняют отрезок 0 ≤ у ≤ π. Приведем гра- фик этой функции (рис. 3.16). Функция у = arctg x определена на интервале -∞ < x < +∞, а значения функции заполняют интервал -(π/2) < у < π/2 (рис. 3.17). Приведем графики некоторых функций, которые получа- ются из основных элементарных функций. График функции у = cos (х − π/4) — косинусоида, сдвинутая вдоль оси абсцис вправо на величину π/4 (рис. 3.18).
Рис. 3.15
Рис. 3.16
Рис. 3.17
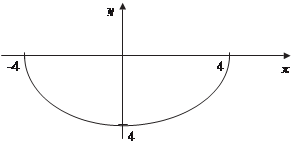
Рис. 3.18 Функция -4 ≤ х ≤ 4. Возведем в квадрвт обе части уравнения
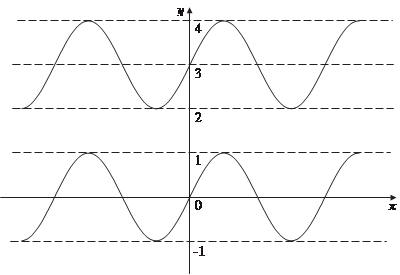
Рис. 3.19 Графиком функции у = sin x + 3 является синусоида, сдвинутая в направлени оси ординат вверх на три единицы (рис. 3.20). Покажем, как строятся графики функций вида y = f (| x |); у = | f (х)|; | у | = f (x). Напомним определение модуля числа:
- х при х < 0.
Рис. 3.20 Для построения графика функции у = f (| x |) на основании определения модуля получим:
f (- x) при х < 0. График данной функции состоит из двух графиков: графи- ка у = f (x) в правой полуплоскости и графика у = f (- x) в левой полуплоскости. Построим график функции.
у = х 2 − 3 | х | +2 = х 2 − 3 х + 2 при х ≥ 0;
Функция у = f (| x |) четная, поэтому для построения ее гра- фика нужно построить график функции у = f (x) для ∀ х > 0 из области ее определения и отразить его симетрично оси ординат (рис. 3.21). Для построения графика функции y = | f (x)| на основании определения модуля получим:
Рис. 3.21
- f (x) при f (x) < 0. Отсюда видно, что для построения графика функции у = | f (x)| достаточно построить график функции у = f (x) для
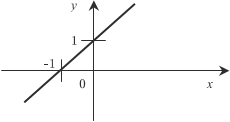
∀ х из области ее определения и ту часть графика функции у = f (x), которая расположена ниже оси абсцисс (f (x) < 0), от- разить симметрично этой оси. Следовательно, график функ- ции у = | f (x)| расположен над осью абсцисс. Например, для пос- троения графика функции у = | х 2 − 4| надо построить график функции у = х 2 − 4 для ∀х и ту часть графика, которая распол- жена ниже оси 0Х (-2 < x < 2), отразить симметрично этой оси (рис. 3.22). Имея в виду, что в формуле | у | = f (x) f (x) ≥ 0 и на основа- нии определения модуля, получим:
- у при у < 0. Теперь перепишем | у | = f (x) в виде у = ± f (x) при f (x) ≥ 0 и сформулируем правило построения графика функции | у | = f (x). Нужно построить график функции у = f (x) для тех х из области ее определения, при которых f (x) ≥ 0 и отразить полученную часть графика симметрично оси абсцисс. Следо- вательно, график функции | у | = f (x) состоит из графиков двух
Рис. 3.22
функций: у = f (x) и у = - f (x) при f (x) ≥ 0. Например, график функции | у | = х имеет вид (рис. 3.23). Рис. 3.23
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 117; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.222.84 (0.012 с.) |


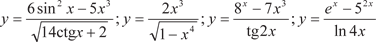
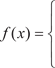
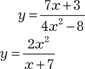 Алгебраическими являются следующие функции:
Алгебраическими являются следующие функции: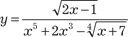
 , y = 5 · 8 x +1.
, y = 5 · 8 x +1.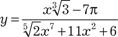 ,
,  ,
,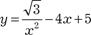 ,
,  .
. ;
;  являются иррациональ- ными.
являются иррациональ- ными.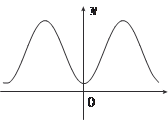 Функция y = f (x) называется четной, если при изменении знака у любого значения аргумента из ее области определения значения функции не изменяется,
Функция y = f (x) называется четной, если при изменении знака у любого значения аргумента из ее области определения значения функции не изменяется,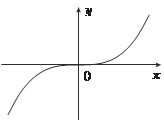 f (x + T) = f (x). (3.1)
f (x + T) = f (x). (3.1)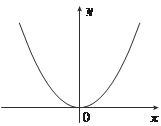 ром функция убывает, — интервалом убывания. Интервалы возрастания и убывания функции называются ин- тервалами монотонности функции, а функция в этих интервалах — моно- тонной. Например, функция y = x 2 на интервале (-∞; 0) монотонно убывает, а на интервале (0; +∞) монотонно воз-
ром функция убывает, — интервалом убывания. Интервалы возрастания и убывания функции называются ин- тервалами монотонности функции, а функция в этих интервалах — моно- тонной. Например, функция y = x 2 на интервале (-∞; 0) монотонно убывает, а на интервале (0; +∞) монотонно воз-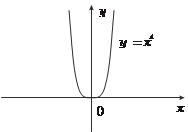

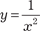
 (рис. 3.9):
(рис. 3.9):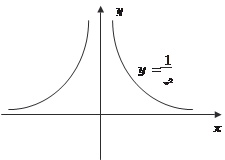


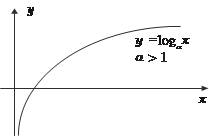

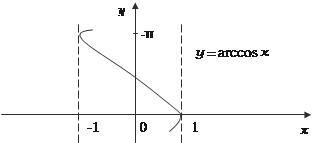
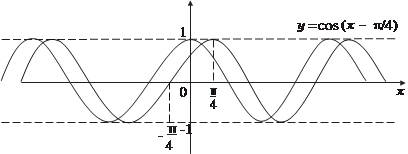
 определена при 16 − х 2 ≥ 0 или при
определена при 16 − х 2 ≥ 0 или при , получаем х 2 + у 2 = 16, а это уравнение окружности с радиусом 4, с центром в начале координат. Так как исходная функция при- нимает только отрицательные значения, то ее графиком будет полуокужность, расположеная ниже оси абсцисс (рис. 3.19).
, получаем х 2 + у 2 = 16, а это уравнение окружности с радиусом 4, с центром в начале координат. Так как исходная функция при- нимает только отрицательные значения, то ее графиком будет полуокужность, расположеная ниже оси абсцисс (рис. 3.19).