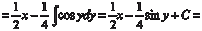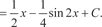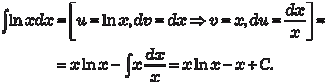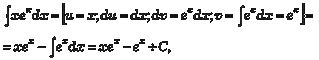Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 5. Элементы интегрального исчисленияСодержание книги
Поиск на нашем сайте Интегральное исчисление — это раздел математического анализа, в котором изучаются свойства и способы вычисления интегралов и их применение. Интегрирование — это действие, обратное дифференци- рованию. Например, с его помощью находится скорость тела по заданному ускорению.
Первообразная и неопределенный интеграл Первообразной от функции y = f (x) на некотором проме- жутке называется функция F (x), производная которой равна исходной функции, т. е. F (x) = f (x). Из этого определения сле- дует, что любая функция по отношению к своей производной является первообразной.
Из данного примера видно, что любая функция будет первообразной для функцией y = x 5. Теперь приведем формулировку основной теоремы о пер- вообразных. Теорема 5.1. Любая непрерывная функция имеет беско- нечное множество первообразных, причем любые две из них друг от друга отличаются постоянным слагаемым [9, 44]. Формула F (x) + C исчерпывает множество всех первооб- разных исходной функции. Геометрически выражение F (x)+ C
Рис. 5.1 Заметим, что первообразную можно находить не только по производной, но и по дифференциалу. Теперь дадим определение неопределенного интеграла.
Отыскание первообразных называется неопределенным интегрированием, а выражение, охватывающие совокупность всех первообразных от данной функции f (x) называется неоп- ределенным интегралом и обозначается так: где f (x) — подынтегральная функция; f (x) dx — подынтегральное выражение; х — переменная интегрирования. Заметим, что f (x) на участке интегрирования должна быть непрерывна;
Таким образом, неопределенный интеграл есть семейство функций F (x) + C, т. е.
Нахождение всех первообразных для данной функции f (x) и называется неопределенным интегрированием. Термин “не- определенное интегрирование” появился, потому что не указы- вается, какая первообразная имеется в виду. Сразу скажем, что интегрирование значительно сложнее дифференцирования. Дифференцирование любых элементар- ныхфункцийпроизводитсяпоопределеннымправилам, аинтег- рирование требует в каждом конкретном случае индивидуаль- ного подхода. Разумеется, есть общие методы интегрирования, некоторые мы рассмотрим далее. Заметим, что производная от любой элементарной функции есть функция элементарная, а про неопределенный интеграл от элементарной функции этого сказать нельзя. Первообразная от элементарной функции мо- жет оказаться и не представимой с помощью конечного числа элементарных функций. Про такие функции говорят, что они не интегрируемы в элементарных функциях. Примерами так называемых неберущихся интегралов являются:
и др.
(5.1)
Найдем неопределенные интегралы от основных элемен- тарных функций, используя для этого таблицу производных от основных элементарных функций (см. главу 4 “Основы диффе- ренциального исчисления”). Например, (sin x) = cos x. Перепишем это равенство в виде
Проинтегрируем обе части последнего равенства и с уче- том третьей формулы (5.1) получим Это и есть табличный интеграл. Точно так же получают и другие табличные интегралы от основных элементарных функций. Приведем таблицу интегралов от основных элементарных функций. Справедливость приведенных формул легко прове- рить дифференцированием.
Добавим формулы интегрирования гиперболических и об- ратных гиперболических функций.
13) 14)
16)
17)
18)
Объединение формул 17 и 18 и дает формулу 11 таблицы не- определенных интегралов. Заметим, что кроме основной таблицы интегралов существуют таблицы интегралов от элементарных и специальных функций, например. (Брычков Ю. А., Маричев О. И., Прудников А. П. Таблицы неопределенных интегралов. — М.: На- ука, 1986; Интегралы и ряды. В 3 т. — М.: Наука, 1986). Задача “взятия” неопределенного интеграла состоит в том, чтобы преобразовать его к табличному. Приведем свойства неопределенного интеграла. 1.
Неопределенный интеграл от алгебраической суммы ко- нечного числа непрерывных функций равен алгебраической сумме неопределенных интегралов от этих функций, т. е. 2. Постоянный множитель подынтегральной функции можно выносить за знак неопределенного интеграла, т. е.
3. Любая формула интегрирования сохраняет свой вид при постановке вместо независимой переменной любой дифферен- цируемой функции от нее, т. е. если
где u = u (x) — любая дифференцируемая функция от x. В силу свойства 3 таблица неопределенных интегралов (ос- новная таблица) будет справедливой независимо от того, явля- ется ли переменная интегрирования независимой переменной или любой дифференцируемой функции от нее, т. е. основная таблица интегралов сразу значительно расширяется [9, 42. 44].
Методы интегрирования 1. Непосредственное интегрирование. Используется таб- лица интегралов, свойства неопределенных интегралов и раз- личные преобразования подынтегрального выражения.
Пример 5.2.
Пример 5.4.
[Воспользуемся формулами cos 2 x = cos2 x − sin2 x,
cos 2 x = 1 − 2sin2 x, 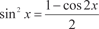 . Последнее выражение подстав- ляем вместо подынтегральной функции] . Последнее выражение подстав- ляем вместо подынтегральной функции]
[Заметим, что d 2 x = 2 dx заменяем 2 х на y, т. е. 2 х = y. ] [Возвращаемся к прежнему аргументу] =
Таким образом, в примере 5.4 использовали еще один ме- тод интегрирования (замена переменной), который более под- робно рассмотрим ниже. 2. Интегрирование по частям. Этот метод следует из фор- мулы дифференцирования произведения двух функций. Пусть u (x) и v (x) — дифференцируемые функции аргу- мента х, тогда имеем (uv) = u v + v u, или d (uv) = v du + u dv, u dv = d (uv) − v du. Интегрируем обе части последнего равенства и получим.
Это и есть формула интегрирования по частям. Этот способ состоит в том, что подынтегральное выраже- ние представляется в виде произведения двух множителей u и dv и заменяется двумя интегрированиями: 1) отыскание v из выражения для dv; 2) отыскание интеграла от vdu. Смысл способа состоит в том, что эти два интегрирования выполнить легче, чем “взять” исходный интеграл. Рассмотрим конкретные примеры применения данного ме- тода.
Пример 5.5. В данном примере выбор u и d v производится одно- значно, но так бывает не всегда.
но если принять то
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 267; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.007 с.) |

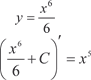 Рассмотрим пример y = x 5. Данная функция служит произ- водной для функции, так как
Рассмотрим пример y = x 5. Данная функция служит произ- водной для функции, так как  и
и 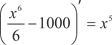 ,
,
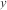 есть семейство кривых (рис. 5.1.), каждая из которых получает- ся путем сдвига одной из кривых вдоль оси 0 у.
есть семейство кривых (рис. 5.1.), каждая из которых получает- ся путем сдвига одной из кривых вдоль оси 0 у.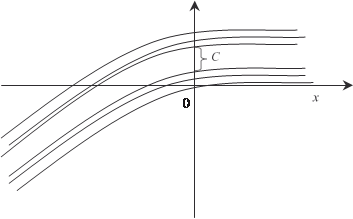
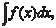
 — знак интеграла.
— знак интеграла.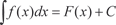
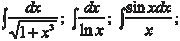
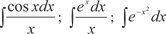
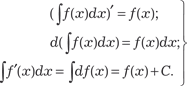

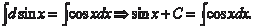
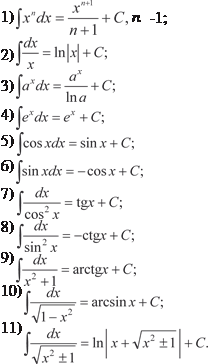
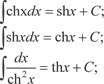 12)
12)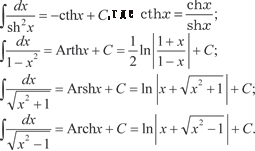 15)
15)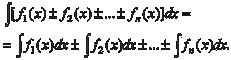
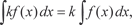
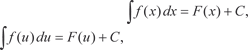 то и
то и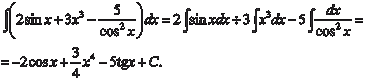
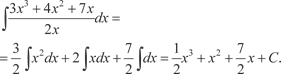
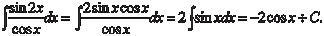
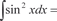
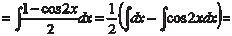
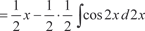 =
=