
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понижение степени подынтегральной функцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Данный приём работает, когда подынтегральные функции нафаршированы синусами и косинусами в чётных степенях. Для понижения степени используют тригонометрические формулы
Пример 7 Найти неопределенный интеграл.
Решение:
В принципе, ничего нового здесь нет, за исключением того, что мы применили формулу
Пример 8 Найти неопределенный интеграл
Это пример для самостоятельного решения, полное решение и ответ – в конце урока.
Далее – пример с повышением степени:
Пример 9 Найти неопределенный интеграл
Сначала решение, потом комментарии:
(1) Готовим подынтегральную функцию для применения формулы (2) Собственно применяем формулу. (3) Возводим знаменатель в квадрат и выносим константу за знак интеграла. Можно было поступить несколько иначе, но так удобнее. (4) Используем формулу (5) В третьем слагаемом снова понижаем степень, но уже с помощью формулы (6) Приводим подобные слагаемые (здесь мы почленно разделили (7) Собственно берём интеграл, правило линейности (8) Причесываем ответ. В неопределенном интеграле нередко ответ можно записать несколькими способами. В только что рассмотренном примере окончательный ответ можно было записать иначе – раскрыть скобки и даже сделать это до интегрирования выражения. То есть вполне допустима следующая концовка примера:
Пример 10 Найти неопределенный интеграл
Это пример решается двумя способами, и у Вас могут получиться д ва разных ответа (точнее, они будут выглядеть совершенно по-разному, но с математической точки зрения являться эквивалентными). Скорее всего, Вы не увидите наиболее рациональный способ и помучаетесь с раскрытием скобок, использованием других тригонометрических формул. Наиболее эффективное решение приведено в конце урока.
Подытоживая параграф, сделаем вывод: любой интеграл вида На практике мне встречались интегралы с 8 и 10 степенями, решать их приходилось
Метод замены переменной
Как уже упоминалось в статье Метод замены переменной в неопределенном интеграле, основной предпосылкой для использования метода замены является тот факт, что в подынтегральном выражении есть некоторая функция
Пример 11 Найти неопределенный интеграл
Смотрим в таблицу производных и замечаем формулы Вопрос можно решить методом научного тыка: если мы неправильно выполним замену, то ничего хорошего не получится. Общий ориентир: в похожих случаях за t нужно обозначить функцию, которая находится в знаменателе. Итак, запомнили:
Прерываем решение и проводим замену
В знаменателе у нас всё хорошо, всё зависит только от, теперь осталось выяснить, во что превратится Для этого находим дифференциал dt:
Или, если короче: Из полученного равенства по правилу пропорции получаем нужное нам выражение:
Итак:
Теперь всё подынтегральное выражение у нас зависит только от t и можно продолжать решение
Готово. Напоминаем, что цель замены – упростить подынтегральное выражение. В данном случае всё свелось к интегрированию степенной функции по таблице.
А сейчас два примера для самостоятельного решения: Пример 12 Найти неопределенный интеграл
Пример 13 Найти неопределенный интеграл
Полные решения и ответы в конце урока.
Пример 14 Найти неопределенный интеграл
Здесь опять в подынтегральном выражении находятся синус с косинусом (функция с производной), но уже в произведении, и возникает дилемма – что обозначать за t, синус или косинус? Можно попытаться провести замену методом научного тыка, и, если ничего не получится, то обозначить за t другую функцию, но есть общий ориентир. Общий научный ориентир: за t нужно обозначить ту функцию, которая, образно говоря, находится в «неудобном положении». Мы видим, что в данном примере, что Поэтому проведем замену:
Пример 15 Найти неопределенный интеграл
Анализируем подынтегральную функцию. Что нужно обозначить за t? Вспоминаем наши ориентиры: 1) Функция, скорее всего, находится в знаменателе; 2) Функция находится в «неудобном положении». Кстати, эти ориентиры справедливы не только для тригонометрических функций. Под оба критерия (особенно под второй) подходит синус, поэтому напрашивается замена В принципе, замену можно уже проводить, но сначала неплохо было бы разобраться, а что делать с
Произведение
Готово.
Общее правило: Если в подынтегральной функции одна из тригонометрических функций (синус или косинус) находится в нечетной степени, то нужно от нечетной степени «откусить» одну функцию, а за t – обозначить другую функцию. Речь идет только об интегралах, где есть косинусы и синусы. В рассмотренном примере в нечетной степени у нас находился косинус, поэтому мы отщипнули от степени один косинус, а за t обозначили синус.
Пример 16 Найти неопределенный интеграл
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
|
||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 3022; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 ,
,  и
и , причем последняя формула чаще используется в обратном направлении, как:
, причем последняя формула чаще используется в обратном направлении, как:  .
.

 , сначала устно берем интеграл от 1, затем – от cos2 x.
, сначала устно берем интеграл от 1, затем – от cos2 x. .
. .
.
 .
. и выполнили сложение
и выполнили сложение  ).
).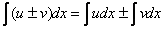 и метод подведения функции под знак дифференциала выполняем устно.
и метод подведения функции под знак дифференциала выполняем устно.

 .
. , где n и m – чётные числа, решается методом понижения степени подынтегральной функции.
, где n и m – чётные числа, решается методом понижения степени подынтегральной функции. и её производная
и её производная  :
: (функции
(функции  .
. ,
,  , то есть, в нашем подынтегральном выражении есть функция и её производная. Однако мы видим, что при дифференцировании косинус и синус взаимно превращаются друг в друга, и возникает вопрос: как выполнить замену переменной и что же обозначать за t – синус или косинус?!
, то есть, в нашем подынтегральном выражении есть функция и её производная. Однако мы видим, что при дифференцировании косинус и синус взаимно превращаются друг в друга, и возникает вопрос: как выполнить замену переменной и что же обозначать за t – синус или косинус?! .
. ;
; .
. .
.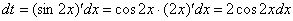

 .
.

 .
. .
. .
. .
.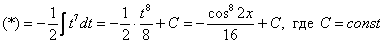
 .
. .
. ? Во-первых, «отщипываем» один косинус:
? Во-первых, «отщипываем» один косинус: .
. мы резервируем под наш «будущий» дифференциал dt. А
мы резервируем под наш «будущий» дифференциал dt. А 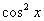 выражаем через синус с помощью основного тригонометрического тождества:
выражаем через синус с помощью основного тригонометрического тождества: . Проводим преобразования:
. Проводим преобразования: Вот теперь замена:
Вот теперь замена: 

 .
.


