Подведение числителя под знак дифференциала
Интегралы, которые мы будем рассматривать, похожи на интегралы предыдущего параграфа, они имеют вид: 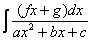 или или 
(коэффициенты a, b и f не равны нулю).
То есть, в числителе у нас появилась линейная функция. Как решать такие интегралы?
Пример 14
Найти неопределенный интеграл
 . .
Пожалуйста, будьте внимательны, сейчас мы рассмотрим типовой алгоритм.
1) Когда дан интеграл вида
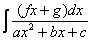 или или 
(где коэффициенты a, b и f не равны нулю), то первое, что мы делаем, это… берём черновик. Дело в том, что сейчас нам предстоит выполнить небольшой подбор.
2) Сформируем числитель подынтегрального выражения тождественными преобразованиями (выразим числитель через знаменатель). Для этого пока просто заключаем выражение, которое находится в данном примере в знаменателе (неважно – под корнем или без корня), под знак дифференциала: 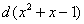 . .
3) Раскрываем дифференциал:
 . .
Смотрим на числитель нашего интеграла: 
Немного разные вещи получились…. А теперь нам нужно подобрать множитель для дифференциала 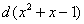 , такой, чтобы при его раскрытии получилось, как минимум, 3 x. В данном случае с подходящим множителем получится: , такой, чтобы при его раскрытии получилось, как минимум, 3 x. В данном случае с подходящим множителем получится:
 . .
4) Для самоконтроля снова раскрываем наш дифференциал:

Снова смотрим на числитель нашего интеграла:
 . Уже ближе, но у нас получилось не «то» слагаемое (+2), а другое: (+3/2). . Уже ближе, но у нас получилось не «то» слагаемое (+2), а другое: (+3/2).
5) К нашему дифференциалу

приписываем слагаемое, которое у нас изначально было в подынтегральной функции:
 . .
– Вычитаем (в данном случае – вычитаем, иногда нужно, наоборот, прибавлять)
наше «не то» слагаемое:

– Обе константы берем в скобки и приписываем справа значок дифференциала:

– Вычитаем (в некоторых примерах нужно сложить) константы:
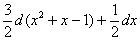 . .
6) Выполняем проверку:

У нас получился в точности числитель подынтегральной функции, значит, подбор выполнен успешно.
Чистовое оформление решения выглядит примерно так:

(1) Выполняем на черновике подбор числителя согласно вышерассмотренному алгоритму. Обязательно выполняем проверку, правильно ли выполнен подбор. При определенном опыте решения интегралов подбор нетрудно выполнить и в уме.
(2) Почленно делим числитель на знаменатель. В практическом решении задач данный шаг можно опускать
(3) Используя свойство линейности, разделяем интегралы. Все константы целесообразно вынести за знаки интегралов.
(4) Первый интеграл фактически является табличным, используем формулу  (константу C припишем позже, когда возьмем второй интеграл). Во втором интеграле выделяем полный квадрат (такой тип интегралов мы рассмотрели в предыдущем параграфе). Остальное дело техники. (константу C припишем позже, когда возьмем второй интеграл). Во втором интеграле выделяем полный квадрат (такой тип интегралов мы рассмотрели в предыдущем параграфе). Остальное дело техники.
И, на закуску, пара примеров для самостоятельного решения – один проще, другой сложнее.
Пример 15
Найти неопределенный интеграл
 . .
Пример 16
Найти неопределенный интеграл
 . .
Для решения Примеров 15 и 16 будет полезен частный случай интегрирования степенной функции, которого нет в нашей справочной таблице:
 . .
Как видите, интегрирование дробей - дело кропотливое, часто приходится применять искусственные приемы и подборы. Но что делать…
Существуют и другие виды дробей, так называемые дробно-рациональные функции, они решаются методом неопределенных коэффициентов. Но это уже тема урока Интегрирование дробно рациональных функций.
Решения и ответы:
Пример 2: Решение:
 . .
Пример 4: Решение:
 . .
Пример 7: Решение:

Пример 8: Решение:
 . .
Пример 10: Решение:
 . .
Пример 13: Решение:
 . .
Пример 15: Решение:

Пример 16: Решение:
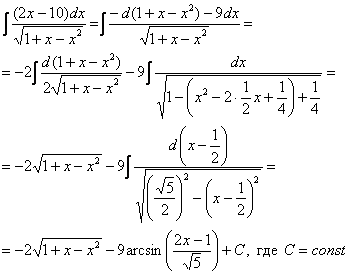 . .
|