
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теперь немного о геометрических иллюзиях.
У людей часто возникают иллюзии, связанные с объемами, которую подметил еще Перельман (не тот, что отказался от премии, а еще в 50-60 гг.) в книге Занимательная геометрия. Посмотрите на плоскую фигуру в решённой задаче – она вроде бы невелика по площади, а объем тела вращения составляет чуть более 50 кубических единиц, что кажется слишком большим. Кстати, среднестатистический человек за всю свою жизнь выпивает жидкость объемом с комнату площадью 18 кв. метров, что, наоборот, кажется слишком маленьким объемом.
Пример 4 Вычислить объем тела, образованного вращением относительно оси OX плоской фигуры, ограниченной линиями Это пример для самостоятельного решения. Обратите внимание, что все дела происходят в полосе
Вычисление объема тела, образованного вращением плоской фигуры вокруг оси OY
Второй параграф будет еще интереснее, чем первый. Задание на вычисление объема тела вращения вокруг оси ординат – тоже достаточно частый гость в контрольных работах. Попутно будет рассмотрена задача о нахождении площади фигуры вторым способом – интегрированием по оси OY, что позволит вам не только улучшить свои навыки, но и научит находить наиболее выгодный путь решения. В этом есть и практический смысл!
Пример 5 Дана плоская фигура, ограниченная линиями 1) Найти площадь плоской фигуры, ограниченной данными линиями. 2) Найти объем тела, полученного вращением плоской фигуры, ограниченной данными линиями, вокруг оси OY. Внимание! Даже если вы хотите ознакомиться только со вторым пунктом, сначала обязательно прочитайте первый! Решение: Задача состоит из двух частей. Начнем с определения площади. 1) Выполним чертёж:
Легко заметить, что функция
Нужная фигура, площадь которой предстоит найти, заштрихована синим цветом. Как найти площадь фигуры? Её можно найти «обычным» способом, который рассматривался в разделе: 7.2.3. Как вычислить площадь фигуры. Причем, площадь фигуры находится, как сумма площадей: - на отрезке [0; 1], – на отрезке [1; 4], Поэтому:
Чем в данном случае плох обычный путь решения? Во-первых, получилось два интеграла. Во-вторых, под интегралами корни, а корни в интегралах – не подарок, к тому же можно запутаться в подстановке пределов интегрирования. На самом деле, интегралы, конечно, не убийственные, но на практике всё бывает значительно печальнее, просто мы подобрали для задачи функции «получше». Есть более рациональный путь решения: он состоит в переходе к обратным функциям и интегрированию по оси OY. Как перейти к обратным функциям? Просто нужно выразить «икс» через «игрек». Сначала разберемся с параболой:
Этого достаточно, но убедимся, что такую же функцию можно вывести из нижней ветки:
Для самопроверки рекомендую устно или на черновике подставить координаты 2-3-х точек параболы в уравнение Теперь смотрим на ось OY и, пожалуйста, периодически наклоняйте голову вправо на 90 градусов по ходу объяснений (это не шутка!). Нужная нам фигура лежит на отрезке [2; 5], оси OY, который ограничен красными пунктирами. При этом на отрезке [2; 5] прямая
Что поменялось в формуле? Только буква, и не более того. Примечание: Пределы интегрирования по оси OY расставлять строго снизу вверх! Находим площадь: На отрезке [2; 5],
Для читателей, сомневающихся в корректности интегрирования, найдём производные:
Получена исходная подынтегральная функция, значит интегрирование выполнено правильно. Ответ: 2) Вычислим объем тела, образованного вращением данной фигуры, вокруг оси OY. Перерисуем чертеж немного в другом оформлении:
Итак, фигура, заштрихованная синим цветом, вращается вокруг оси OY. В результате получается «зависшая бабочка», которая вертится вокруг своей оси (ординат).
Для нахождения объема тела вращения будем интегрировать по оси OY. Сначала нужно перейти к обратным функциям. Это уже сделано и подробно расписано в предыдущем пункте. Теперь снова наклоняем голову вправо и изучаем нашу фигуру. Очевидно, что объем тела вращения, следует найти как разность объемов. Вращаем фигуру, обведенную красным цветом, вокруг оси OY, в результате получается усеченный конус. Обозначим этот объем через V 1. Вращаем фигуру, обведенную зеленым цветом, вокруг оси OY и обозначаем через V 2 объем полученного тела вращения. Объем нашей бабочки равен разности V = V 1 - V 2. Используем формулу для нахождения объема тела вращения:
В чем отличие от формулы предыдущего параграфа? Только в букве.
А вот и преимущество интегрирования, о котором мы говорили. Гораздо легче найти
чем предварительно возводить подынтегральную функцию в 4-ую степень. Ответ: Заметьте, что если эту же плоскую фигуру вращать вокруг оси OX, то получится совершенно другое тело вращения, другого, естественно, объема.
Пример 6 Дана плоская фигура, ограниченная линиями 1) Перейти к обратным функциям и найти интегрированием по переменной y площадь плоской фигуры, ограниченной данными линиями. 2) Вычислить объем тела, полученного вращением плоской фигуры, ограниченной данными линиями, вокруг оси OY. Правильный ответ:
Это пример для самостоятельного решения. Полное же решение двух предложенных пунктов задания в конце урока.
Да, и не забывайте наклонять голову направо, чтобы разобраться в телах вращения и в пределах интегрирования!
Пример 7 Вычислить объем тела, образованного вращением вокруг оси OY фигуры, ограниченной кривыми
Решение: Выполним чертеж:
Попутно знакомимся с графиками некоторых других функций. Такой вот интересный график чётной функции
Для цели нахождения объема тела вращения достаточно использовать правую половину фигуры, которая заштрихована синим цветом. Обе функции являются четными, их графики симметричны относительно оси OY, симметрична и наша фигура. Таким образом, заштрихованная правая часть, вращаясь вокруг оси OY, непременно совпадёт с левой незаштрихованной частью. Перейдем к обратным функциям, то есть выразим «иксы» через «игреки»:
Обратите внимание, что правой ветке параболы y = x 2 соответствует обратная функция К слову, та же история и с функций
Не всегда бывает сразу понятно, какую обратную функцию выбрать:
В действительности мы всегда страхуемся, подставляя в найденную обратную функцию пару точек графика. Теперь наклоняем голову вправо и замечаем следующую вещь: – на отрезке [0; 1] над осью OY расположен график функции – на отрезке [1; 2] над осью OY расположен график функции Логично предположить, что объем тела вращения нужно искать уже как сумму объемов тел вращений. Используем формулу:
В данном случае:
Ответ:
Решения и ответы: Пример 2: Решение: Выполним чертеж:
Объем тела вращения:
Ответ:
Пример 4: Решение: 1) Выполним чертеж:
Объем тела вращения вычислим как разность объемов при помощи формулы:
В данном случае:
Ответ: Примечание: Обратите внимание на использование свойства линейности – в данном случае при интегрировании выгодно превратить два интеграла в один. Это можно сделать, поскольку константы перед интегралами и пределы интегрирования одинаковы, а затем использовать формулу косинуса двойного угла. Пример 6: Решение: 1) Выполним чертёж:
Перейдем к обратной функции:
На отрезке [-ln2; 0],
Ответ: 2) Вычислим объем тела, образованного вращением данной фигуры, вокруг оси OY. Объем тела вращения найдем как разность объемов тел вращения при помощи формулы
Ответ:
Несобственные интегралы. Примеры решений
К изучению несобственных интегралов лучше приступать в последнюю очередь в ходе изучения интегрального исчисления функции одной переменной. Читатель данного урока должен быть хорошо подкован в неопределенных интегралах, определенных интегралах, уметь находить площадь плоской фигуры с помощью определенного интеграла. Кроме того, потребуются знания простейших пределов и графиков элементарных функций. По логике изложения материала эта статья является продолжением уроков определенный интеграл, вычисление площади фигуры. Тема несобственных интегралов – очень хорошая иллюстрация тому, как важно не запускать высшую математику и другие точные науки. Образно говоря, несобственный интеграл – это «продвинутый» определенный интеграл, к тому же у несобственного интеграла есть очень хороший геометрический смысл. Что значит вычислить несобственный интеграл? Вычислить несобственный интеграл – это значит найти ЧИСЛО, точнее, предел последовательности, или доказать, что он расходится, то есть получить в итоге бесконечность вместо числа. Несобственные интегралы бывают двух видов: первого и второго рода.
|
|||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 161; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.239.110 (0.049 с.) |
 ,
,  , где
, где  .
. ,
,  ,
, 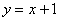 .
.
 ;
; .
. .
. .
. .
.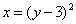 , они обязательно должны удовлетворять данному уравнению. С уравнением прямой линии всё проще:
, они обязательно должны удовлетворять данному уравнению. С уравнением прямой линии всё проще:  .
. расположена выше параболы
расположена выше параболы  , то есть площадь фигуры следует найти по уже знакомой вам формуле:
, то есть площадь фигуры следует найти по уже знакомой вам формуле: .
. , поэтому:
, поэтому: .
. .
.

 .
. .
. ,
,
 ,
,  и осью OX.
и осью OX.
 ;
;  .
.

 . Левой неиспользуемой ветке параболы соответствует обратная функция
. Левой неиспользуемой ветке параболы соответствует обратная функция  . В таких случаях нередко возникают сомнения, какую же функцию выбрать? Сомнения легко, развеиваются, возьмите любую точку правой ветки и подставьте ее координаты в функцию
. В таких случаях нередко возникают сомнения, какую же функцию выбрать? Сомнения легко, развеиваются, возьмите любую точку правой ветки и подставьте ее координаты в функцию  .
. или
или  .
.





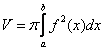



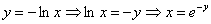
 , поэтому:
, поэтому:






