
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Особенности вычисления частных производныхСодержание книги
Поиск на нашем сайте
Подведем итог, чем же отличается нахождение частных производных от нахождения «обычных» производных функции одной переменной: 1) Когда мы находим частную производную 2) Когда мы находим частную производную 3) Правила и таблица производных элементарных функций справедливы и применимы для любой переменной (
Шаг второй. Находим частные производные второго порядка. Их четыре. Обозначения:
В понятии второй производной нет ничего сложного. Говоря простым языком, вторая производная – это производная от первой производной. Для наглядности я перепишу уже найденные частные производные первого порядка:
Сначала найдем смешанные производные:
Как видите, всё просто: берем частную производную Аналогично:
Для практических примеров, когда все частные производные непрерывны, справедливо следующее равенство:
Таким образом, через смешанные производные второго порядка очень удобно проверить, а правильно ли мы нашли частные производные первого порядка. Находим вторую производную по «икс». Никаких изобретений, берем
Аналогично:
Следует отметить, что при нахождении
Пример 2 Найти частные производные первого и второго порядка функции Это пример для самостоятельного решения (ответ в конце урока).
При определенном опыте частные производные из примеров №№1,2 будут решаться Вами устно. Переходим к более сложным примерам. Пример 3 Найти частные производные первого порядка функции Решение: Находим частные производные первого порядка:
Обратите внимание на подстрочный индекс: Дальнейшие комментарии: (1) Выносим все константы за знак производной. В данном случае (2) Не забываем, как правильно дифференцировать корни.
(1) Выносим все константы за знак производной, в данной случае константой является (2) Под штрихом у нас осталось произведение двух функций, следовательно, нужно использовать правило дифференцирования произведения (3) Не забываем, что Теперь находим смешанные производные второго порядка:
Запишем полный дифференциал Полный дифференциал первого порядка функции двух переменных имеет вид:
В данном случае:
То есть, в формулу нужно просто подставить уже найденные частные производные первого порядка. Значки дифференциалов
Пример 4 Найти частные производные первого порядка функции Это пример для самостоятельного решения. Полное решение и образец оформления задачи – в конце урока. Рассмотрим серию примеров, включающих в себя сложные функции.
Пример 5 Найти частные производные первого порядка функции Записать полный дифференциал Решение:
(1) Применяем правило дифференцирования сложной функции (2) Здесь используем свойство корней: Аналогично: Запишем полный дифференциал первого порядка:
Пример 6 Найти частные производные первого порядка функции Записать полный дифференциал Это пример для самостоятельного решения (ответ в конце урока). Полное решение не привожу, так как оно достаточно простое Довольно часто все вышерассмотренные правила применяются в комбинации.
Пример 7 Найти частные производные первого порядка функции
(1) Используем правило дифференцирования суммы. (2) Первое слагаемое в данном случае считается константой, поскольку в выражении (Знаете, всегда приятно, когда дробь удается превратить в ноль). Для второго слагаемого применяем правило дифференцирования произведения. Кстати, в алгоритме ничего бы не изменилось, если бы вместо Найдем теперь частную производную по y:
(1) В первом слагаемом и в числителе и в знаменателе содержится «игрек», следовательно, нужно использовать правило дифференцирования частного: Для тех читателей, которые мужественно добрались почти до конца урока, расскажу старый мехматовский анекдот для разрядки.
Однажды в пространстве функций появилась злобная производная и как пошла всех дифференцировать. Все функции разбегаются кто куда, никому не хочется превращаться! И только одна функция никуда не убегает. Подходит к ней производная и спрашивает: – А почему это ты от меня никуда не убегаешь? – Ха. А мне всё равно, ведь я «е в степени икс», и ты со мной ничего не сделаешь! На что злобная производная с коварной улыбкой отвечает: – Вот здесь ты ошибаешься, я тебя продифференцирую по «игрек», так что быть тебе нулем. (Кто понял анекдот, тот освоил производные, минимум, на «тройку»).
Пример 8 Найти частные производные первого порядка функции Это пример для самостоятельного решения. Полное решение и образец оформления задачи – в конце урока.
Пример 9 Дана функция двух переменных Это пример для самостоятельного решения. Полное решение и образец оформления где-то рядом. Решения и ответы: Пример 2:
Пример 4: Ссылка для просмотра ниже.
Пример 6:
|
||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 485; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.007 с.) |

 , то переменная
, то переменная считается константой.
считается константой. , то переменная
, то переменная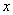 считается константой.
считается константой. или
или  – вторая производная по «икс»
– вторая производная по «икс»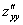 или
или  – вторая производная по «игрек»
– вторая производная по «игрек» или
или  – смешанная производная «по икс игрек»
– смешанная производная «по икс игрек» или
или  – смешанная производная «по игрек икс»
– смешанная производная «по игрек икс»







 . Проверить, что
. Проверить, что  .
.
 , рядом с «иксом» не возбраняется в скобках записывать, что
, рядом с «иксом» не возбраняется в скобках записывать, что  , а, значит, и их произведение
, а, значит, и их произведение  считается постоянным числом.
считается постоянным числом.
 .
. .
. .
.

 .
.
 и
и  в этой и похожих ситуациях по возможности лучше записывать в числителях:
в этой и похожих ситуациях по возможности лучше записывать в числителях:
 . Проверить, что
. Проверить, что  .
.
 (внутренняя функция) у нас не меняется.
(внутренняя функция) у нас не меняется. , выносим константу
, выносим константу  за знак производной, а корень
за знак производной, а корень  представляем в нужном для дифференцирования виде.
представляем в нужном для дифференцирования виде.

 .
. .
.
 нет ничего, зависящего от «икс» – только «игреки».
нет ничего, зависящего от «икс» – только «игреки». была дана функция
была дана функция  – важно, что здесь мы имеем произведение двух функций, КАЖДАЯ из которых зависит от «икс», поэтому нужно использовать правило дифференцирования произведения. Для третьего слагаемого применяем правило дифференцирования сложной функции.
– важно, что здесь мы имеем произведение двух функций, КАЖДАЯ из которых зависит от «икс», поэтому нужно использовать правило дифференцирования произведения. Для третьего слагаемого применяем правило дифференцирования сложной функции.
 . Второе слагаемое зависит ТОЛЬКО от «икс», значит,
. Второе слагаемое зависит ТОЛЬКО от «икс», значит,  .
. . Найти все частные производные первого и второго порядков.
. Найти все частные производные первого и второго порядков. ,
,  ,
,  ,
, 
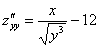
 ,
,  ,
, 



