
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгебраическая форма комплексного числа. Алгебра комплексных чисел
Комплексное число, как упорядоченная пара чисел, представимо как в виде точки на комплексной плоскости, так и в виде z = a + bi, – это и есть алгебраическая форма комплексного числа. Почему речь зашла о форме? Дело в том, что существуют еще и тригонометрическая, и показательная формы комплексного числа, о которых пойдет речь далее. Действия с комплексными числами не представляют особых сложностей и мало чем отличаются от обычной алгебры. Необходимо только помнить, что алгебраические действия должны производиться одновременно с обеими частями упорядоченной пары.
Сложение комплексных чисел Пример 1: Сложить два комплексных числа Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:
Просто, не правда ли? Действие настолько очевидно, что не нуждается в дополнительных комментариях. Таким нехитрым способом можно найти сумму любого количества слагаемых: просуммировать действительные части и просуммировать мнимые части. Для комплексных чисел справедливо правило первого класса:
Вычитание комплексных чисел Пример 2: Найти разности комплексных чисел Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака: Результат не должен смущать, у полученного числа две, а не три части. Просто действительная часть – составная: Рассчитаем вторую разность:
Здесь действительная часть тоже составная: Чтобы не было какой-то недосказанности, приведём пример с «нехорошей» мнимой частью:
Умножение комплексных чисел Настал момент познакомить вас со знаменитым равенством:
Пример 3: Найти произведение комплексных чисел Очевидно, что произведение следует записать так:
Что напрашивается? Напрашивается раскрыть скобки по правилу умножения многочленов. Так и нужно сделать! Все алгебраические действия вам знакомы, главное, помнить, что Повторим школьное правило умножения многочленов: Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена. Распишем подробно:
Надеюсь, всем было понятно, что В учебной литературе легко найти специальную формулу для вычисления произведения комплексных чисел и вывод знаменитого равенства для i. Если хотите, пользуйтесь, но подход с умножением многочленов более понятен. Формулу приводить не буду, считаю, что в данном случае это - забивание головы опилками.
Деление комплексных чисел Пример 4: Даны комплексные числа Составим частное:
Деление чисел осуществляется методом умножения знаменателя и числителя на комплексно сопряженное знаменателю выражение, чтобы в знаменателе получилось действительное число. Вспоминаем бородатую формулу Согласно правилу, знаменатель нужно умножить на
Далее в числителе нужно раскрыть скобки, т. е. перемножить два числа по правилу, рассмотренному в предыдущем пункте. А в знаменателе воспользоваться формулой Распишем подробно:
Пример мы подобрали здесь «хороший», если же взять два числа «от балды», то в результате деления почти всегда получатся дроби, что-нибудь вроде В ряде случаев перед делением дробь целесообразно упростить, например, рассмотрим частное чисел:
Для любителей упростить это частное приведём правильный ответ: i.
Пример 5: Дано комплексное число Приём тот же самый – умножаем знаменатель и числитель на сопряженное знаменателю выражение. Снова смотрим на формулу (a - b)(a + b) = a 2 - b 2. В знаменателе уже есть (a + b), поэтому знаменатель и числитель нужно помножить на сопряженное выражение (a - b), то есть на
Пример 6: Даны два комплексных числа z 1 = 5 + 2 i, z 2 = 2 – 5 i. Найти их сумму, разность, произведение и частное. Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Иногда для решения предлагается навороченный пример, где нужно выполнить много действий с комплексными числами. Никакой паники: будьте внимательны, соблюдайте правила алгебры, обычный алгебраический порядок действий, и помните, что: i 2=-1.
|
||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 179; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.160.154 (0.01 с.) |
 ,
, 

 , – то есть «от перестановки слагаемых сумма не меняется».
, – то есть «от перестановки слагаемых сумма не меняется». и
и 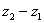 , если
, если 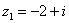 ,
, 
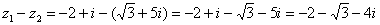 .
.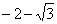 . Для наглядности ответ можно переписать так:
. Для наглядности ответ можно переписать так:  .
.
 .
. . Вот здесь без скобок уже не обойтись.
. Вот здесь без скобок уже не обойтись.
 ,
,  .
.

 . Внимание, и еще раз внимание, чаще всего ошибку допускают в знаках. Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство:
. Внимание, и еще раз внимание, чаще всего ошибку допускают в знаках. Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство:  .
. ,
,  . Найти частное
. Найти частное  .
. .
. и смотрим на наш знаменатель:
и смотрим на наш знаменатель:  . В знаменателе уже есть
. В знаменателе уже есть 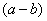 , поэтому комплексно сопряженным выражением в данном случае является
, поэтому комплексно сопряженным выражением в данном случае является  , то есть
, то есть  .
. .
.
 .
. . Перед делением избавляемся от лишних минусов: в числителе и в знаменателе выносим минусы за скобки и сокращаем эти минусы:
. Перед делением избавляемся от лишних минусов: в числителе и в знаменателе выносим минусы за скобки и сокращаем эти минусы: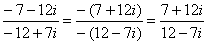 .
. . Записать данное число в алгебраической форме (т.е. в форме a + bi).
. Записать данное число в алгебраической форме (т.е. в форме a + bi). :
:



