
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Любой чертеж графика функции начинается с координатных осей.Содержание книги
Поиск на нашем сайте
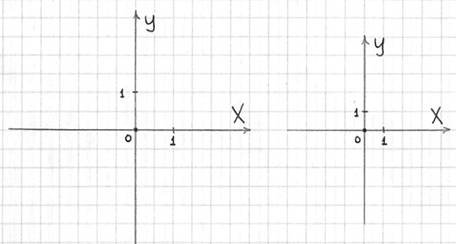
Чертежи бывают двухмерными и трехмерными. Сначала рассмотрим двухмерный случай декартовой прямоугольной системы координат:
1) Чертим координатные оси. Чертить всегда стараемся аккуратно и не криво. Стрелочки тоже не должны быть похожи на бороду Папы Карло. 2) Подписываем оси. Не забываем подписывать оси. 3) Задаем размерность по осями: рисуем ноль и две единички. При выполнении чертежа самая удобная и часто встречающаяся размерность: 1 единица = 2 клеточки (чертеж слева). Я рекомендую Вам по возможности всегда придерживаться именно такой размерности. Но, время от времени случается так, что чертеж не вмещается на тетрадный лист – тогда размерность уменьшаем: 1 единица = 1 клеточка (чертеж справа). Редко-редко, но бывает, что размерность чертежа приходиться уменьшать (или увеличивать) еще больше. НЕ НУЖНО по осям проставлять все значения: …-5, -4, -3, -1, 0, 1, 2, 3, 4, 5, …. Ибо координатная плоскость – не памятник Лобачевскому, а студент – не голубь. Ставим ноль и две единицы по осям. Как говорят математики, это необходимо и достаточно. Размерность можно задать и произвольно, например, поставить 0 и – 1, –1 – по осям, но существуют некоторые стандарты, которых целесообразно придерживаться. Предполагаемые размеры чертежа лучше оценить еще ДО построения чертежа. Так, например, если в задании требуется начертить треугольник с вершинами Кстати, о сантиметрах и тетрадных клетках. Правда ли, что в 30 тетрадных клетках содержится 15 сантиметров? Отмерьте в тетради для интереса 15 сантиметров линейкой. В СССР, возможно, это было правдой… Интересно отметить, что если отмерить эти самые сантиметры по горизонтали и вертикали, то результаты (в клетках) будут разными! Строго говоря, современные тетради не клетчатые, а прямоугольные. Возможно, это покажется ерундой, но, чертить, например, окружность циркулем при таких раскладах очень неудобно. К слову о качестве, или краткая рекомендация по канцтоварам. На сегодняшний день большинство тетрадей в продаже, плохих слов не говоря, - это полное безобразие. По той причине, что они промокают, причём не только от гелевых, но и от шариковых ручек! На бумаге экономят. Для оформления контрольных работ рекомендую использовать тетради Архангельского ЦБК (18 листов, клетка) или «Пятёрочку», правда, она дороже. Ручку желательно выбрать гелевую, даже самый дешевый китайский гелевый стержень намного лучше, чем шариковая ручка, которая - то мажет, а то дерёт бумагу. Единственной «конкурентоспособной» шариковой ручкой на моей памяти является «Эрих Краузе». Она пишет чётко, красиво и стабильно – что с полным стержнем, что с практически пустым. Немецкое качество.
Трехмерный случай
Здесь почти всё так же. 1) Чертим координатные оси. Стандарт: ось 2) Подписываем оси. 3) Задаем размерность по осям. Размерность по оси OX – в два раза меньше, чем размерность по другим осям. Также обратите, внимание, что на правом чертеже размерность задана нестандартно – по оси OX двойкой, а не единицей. С нашей точки зрения, так точнее, и, главное, быстрее и удобнее – не нужно под микроскопом выискивать середину клеточки. При выполнении трехмерного чертежа опять же желательно придерживаться размерности 1 единица = 2 клеточки (чертеж слева). Для чего существует эти правила? Правила, как известно, существуют для того, чтобы их нарушать! Чем я сейчас и займусь. Дело в том, что все последующие чертежи статьи будут выполнены мной в Экселе, и, координатные оси будут выглядеть некорректно с точки зрения правильного оформления. Можно было бы начертить все графики от руки, но MS Excel их начертит гораздо точнее.
График линейной функции Линейная функция задается уравнением Пример 1 Построить график функции Если Берем еще какую-нибудь точку, например, 1. Если При оформлении заданий координаты точек обычно сводятся в таблицу:
А сами значения рассчитываются устно или на черновике, калькуляторе. Две точки найдены, выполним чертеж:
Не лишним будет вспомнить частные случаи линейной функции:
Обратите внимание, как расположены подписи, подписи не должны допускать разночтений при изучении чертежа. В данном случае крайне нежелательно было постаить подпись рядом с точкой пересечения прямых 1) Линейная функция вида 2) Уравнение вида 3) Уравнение вида Некоторые спросят, ну зачем вспоминать 6 класс?! Так-то оно, может и так, только за годы практики я встретил добрый десяток студентов, которых ставила в тупик задача построения графика вроде Построение прямой – самое распространенное действие при выполнении чертежей.
|
||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 367; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.248.214 (0.01 с.) |

 ,
,  ,
, 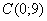 , то совершенно понятно, что популярная размерность 1 единица = 2 клеточки не подойдет. Почему? Посмотрим на точку
, то совершенно понятно, что популярная размерность 1 единица = 2 клеточки не подойдет. Почему? Посмотрим на точку 
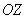 – направлена вверх, ось
– направлена вверх, ось  – направлена вправо, ось
– направлена вправо, ось 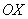 – влево вниз строго под углом 45 градусов.
– влево вниз строго под углом 45 градусов. . График линейной функций представляет собой прямую линию. Для того, чтобы построить прямую, достаточно знать две точки.
. График линейной функций представляет собой прямую линию. Для того, чтобы построить прямую, достаточно знать две точки. . Найдем две точки. В качестве одной из точек выгодно выбрать ноль.
. Найдем две точки. В качестве одной из точек выгодно выбрать ноль. , то
, то 
 , то
, то 



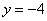 ,
,  (
( ) выражает прямую пропорциональную зависимость. Например,
) выражает прямую пропорциональную зависимость. Например,  . График прямой пропорциональности всегда проходит через начало координат. Таким образом, построение прямой упрощается – достаточно найти всего одну точку.
. График прямой пропорциональности всегда проходит через начало координат. Таким образом, построение прямой упрощается – достаточно найти всего одну точку.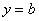 задает прямую, параллельную оси
задает прямую, параллельную оси  . График функции строится сразу, без нахождения всяких точек. То есть, запись
. График функции строится сразу, без нахождения всяких точек. То есть, запись  задает прямую, параллельную оси
задает прямую, параллельную оси 


