
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
При этом сам значок предела перемещаем в показатель.Содержание книги
Поиск на нашем сайте
Далее, отметки карандашом я не делаю, принцип оформления, думаю, понятен.
Пример 7 Найти предел Внимание! Предел подобного типа встречается очень часто, пожалуйста, очень внимательно изучите данный пример. Пробуем подставить бесконечно большое число в выражение, стоящее под знаком предела:
В результате получена неопределенность
Теперь можно почленно разделить числитель на знаменатель:
Вроде бы основание стало напоминать
Таким образом, основание приняло вид
Наконец-то долгожданное
Но на этом мучения не закончены, в показателе у нас появилась неопределенность вида
Готово. А сейчас мы рассмотрим модификацию второго замечательного предела. Напомню, что второй замечательный предел выглядит следующим образом:
Пример 8 Найти предел Сначала (мысленно или на черновике) пробуем подставить ноль (бесконечно малое число) в выражение, стоящее под знаком предела:
В результате получена знакомая неопределенность
Выражение
Еще не всё, в показателе у нас появилась неопределенность вида
Косинус нуля стремится к единице (не забываем помечать карандашом), поэтому он просто пропадает в произведении:
А что такое Как видите, в практических заданиях на вычисление пределов нередко требуется применять сразу несколько правил и приемов. В 90-95% на зачете, экзамене Вам встретится первый замечательный предел или второй замечательный предел. Как быть, если попался «экзотический» замечательный предел? (со списком всех замечательных пределов можно ознакомиться в соответствующей методичке). Ничего страшного, практически все выкладки, приёмы решения для первого замечательного предела справедливы и для остальных замечательных пределов. Нужно решать их по аналогии. Да, так чему же равен предел Если у Вас получился ответ
Производные функций
Как найти производную, как взять производную? На данном уроке мы научимся находить производные функций. Но перед изучением данной страницы я настоятельно рекомендую ознакомиться с методическим материалом Горячие формулы школьного курса математики. Справочное пособие можно открыть или закачать на странице Математические формулы и таблицы. Также оттуда нам потребуется Таблица производных, ее лучше распечатать, к ней часто придется обращаться, причем, не только сейчас, но и в оффлайне. Есть? Приступим. У меня для Вас есть две новости: хорошая и очень хорошая. Хорошая новость состоит в следующем: чтобы научиться находить производные совсем не обязательно знать и понимать, что такое производная. Если Вас интересует теоретическое определение производной функции, математический, физический, геометрический смысл производной – поищите в Интернете, информации море. Наша же задача научиться находить эти самые производные. Очень хорошая новость состоит в том, что научиться брать производные не так сложно, существует довольно чёткий алгоритм решения (и объяснения) этого задания, интегралы или пределы, например, освоить труднее.
|
||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 440; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

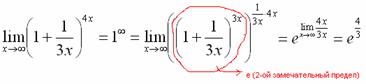
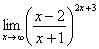

 . Но второй замечательный предел применим к неопределенности вида
. Но второй замечательный предел применим к неопределенности вида  . Что делать? Нужно преобразовать основание степени. Рассуждаем так: в знаменателе у нас
. Что делать? Нужно преобразовать основание степени. Рассуждаем так: в знаменателе у нас  , значит, в числителе тоже нужно организовать
, значит, в числителе тоже нужно организовать 

 , но у нас знак «минус» да и тройка какая-то вместо единицы. Поможет следующее ухищрение, делаем дробь трехэтажной:
, но у нас знак «минус» да и тройка какая-то вместо единицы. Поможет следующее ухищрение, делаем дробь трехэтажной:
 .
. . Снова исполняем наш искусственный прием: возводим основание степени в
. Снова исполняем наш искусственный прием: возводим основание степени в  , и, чтобы выражение не изменилось – возводим в обратную дробь
, и, чтобы выражение не изменилось – возводим в обратную дробь  :
:
 устроено, с чистой совестью превращаем его в букву
устроено, с чистой совестью превращаем его в букву  :
:
 , раскрывать такую неопределенность мы научились на уроке Пределы. Примеры решений. Делим числитель и знаменатель на
, раскрывать такую неопределенность мы научились на уроке Пределы. Примеры решений. Делим числитель и знаменатель на  :
:
 . Однако на практике время от времени можно встретить его «перевёртыш», который в общем виде записывается так:
. Однако на практике время от времени можно встретить его «перевёртыш», который в общем виде записывается так:


 . С помощью знакомого искусственного приема организуем в показателе степени конструкцию
. С помощью знакомого искусственного приема организуем в показателе степени конструкцию  :
:
 со спокойной душой превращаем в букву
со спокойной душой превращаем в букву 
 . Раскладываем тангенс на синус и косинус (ничего не напоминает?):
. Раскладываем тангенс на синус и косинус (ничего не напоминает?):

 и к чему оно стремится, нужно уже знать, иначе «двойка»!
и к чему оно стремится, нужно уже знать, иначе «двойка»! ?
? , значит в понимании высшей математики не всё так безнадежно =).
, значит в понимании высшей математики не всё так безнадежно =).


