
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вынесение минуса из матрицы (внесение минуса в матрицу).Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Вернемся к нашей матрице
Как вы наверняка заметили, в данной матрице слишком много отрицательных чисел. Это очень неудобно с точки зрения выполнения различных действий с матрицей, неудобно писать столько минусов, да и просто в оформлении некрасиво выглядит. Проведем «тождественное преобразование» матрицы, которое её не изменит. Вынесем минус за пределы матрицы, сменив у КАЖДОГО элемента матрицы знак:
У нуля, как Вы понимаете, знак не меняется, ноль – он и в Африке ноль. Обратный пример:
Внесем минус в матрицу, сменив у КАЖДОГО элемента матрицы знак:
Ну вот, гораздо симпатичнее получилось. И, самое главное, выполнять какие-либо действия с матрицей будет ПРОЩЕ. Потому что есть такая математическая народная примета: чем больше минусов – тем больше путаницы и ошибок.
2) Умножение матрицы на число. Пример: Преобразовать:
Как видим, чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку. Пример: Преобразовать:
применив умножение матрицы на дробь.
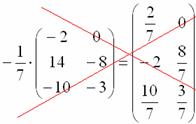
Сначала рассмотрим то, чего делать НЕ НАДО (это правильно, но усложняет вид):
Вносить дробь в матрицу НЕ НУЖНО, во-первых, это только затрудняет дальнейшие действия с матрицей, во-вторых, затрудняет проверку решения преподавателем (особенно, если И, тем более, НЕ НАДО делить каждый элемент матрицы на минус семь:
Что желательно сделать в этом примере – это внести минус в матрицу:
А вот если бы ВСЕ элементы матрицы делились на 7 без остатка, то тогда можно (и нужно!) было бы поделить.
Пример:
В этом случае можно и НУЖНО умножить все элементы матрицы на (1/2), так как все числа матрицы делятся на 2 без остатка.
Примечание: В теории высшей математики школьным понятием «деление» обычно не пользуются. Вместо фразы «это поделить на это» всегда можно сказать «это умножить на дробь». Любое деление – это частный случай умножения.
Транспонирование матрицы Определение: Чтобы транспонировать матрицу, нужно строки исходной матрицы записать в столбцы транспонированной матрицы. А именно: строку номер «m» исходной матрицы в столбец номер «m» транспонированной матрицы. После транспонирования новой матрице выдают особый знак: к символу исходной матрицы справа сверху добавляют большую букву T, или штрих. Следствие: Если исходная матрица Am n – порядка (размером) «m на n», то матрица, транспонированная к исходной матрице, будет размером «n на m» и иметь вид ATn∙т. Следствие: При операции транспонирования элементы на главной диагонали матрицы (от верхнего левого до нижнего правого) остаются неизменными.
Пример: Транспонировать матрицу Внимание: не «транспортировать», не «трансвестировать», а «транспонировать»! Строка здесь всего одна и, согласно правилу, её нужно записать в столбец:
Таким образом, DT – это матрица, транспонированная к исходной матрице D. Подчеркнём, что исходная матрица A и транспонированная матрица AT - это две различные, в общем случае, матрицы. A = AT только в особых случаях: если A – симметричная матрица, когда элементы, симметричные относительно главной диагонали исходной матрицы, равны.
Пример пошаговый: Транспонировать матрицу Примечание: В матрице B на главной диагонали расположены элементы: {-1; 4; -6}.
Заполняем места элементов транспонированной матрицы BT. Другими словами, строим эту самую транспонированную матрицу. Сначала переписываем первую строку B - в первый столбец BT.:
Потом переписываем вторую строку во второй столбец: И, наконец, переписываем третью строку в третий столбец:
Примечание: Транспонировать – это значит прибить матрицу в левом верхнем элементе и повернуть её (исходную матрицу) вокруг главной диагонали на 180°.
Сумма (разность) матриц. Сумма матриц - действие несложное. НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ. Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой.
Определение: Для того чтобы получить матрицу, равную сумме (разности) двух исходных матриц, необходимо сложить (вычесть) их соответствующие элементы: Пример: Сложить матрицы В соответствии с определением, запишем:
Для разности матриц, аналогично, находим разность соответствующих элементов: Пример: Найти разность матриц
А как решить данный пример проще, чтобы не запутаться? Целесообразно избавиться от лишних минусов, для этого внесем минус в матрицу H:
Примечание: В теории высшей математики школьного понятия «вычитание» нет. Вместо фразы «из этого вычесть это» всегда можно сказать «к этому прибавить отрицательное число». То есть, вычитание – это частный случай сложения.
Умножение матриц. Скажем сразу, правило умножения матриц (есть в любом учебнике по алгебре) выглядит очень странно для неподготовленного слушателя, но мы объясним это на конкретных примерах. Прежде всего: «Какие матрицы можно умножать?» Следствие (из строгого определения): Для умножения матрицы K на матрицу L слева необходимо, чтобы число столбцов матрицы K равнялось числу строк матрицы L.
Пример: Можно ли умножить матрицу
А вот если, в данном случае, матрицы переставить местами, то умножение уже невозможно!
Не так уж редко встречаются задания с подвохом, когда студенту предлагается умножить матрицы, умножение которых заведомо невозможно. Следует отметить, что в ряде случаев можно умножать матрицы и так, и так, но с разным результатом, т. к. в общем случае KL ¹ LK. Например, для матриц
Как умножать матрицы? Умножение матриц лучше объяснить на конкретных примерах, так как строгое определение введет в замешательство (или помешательство) большинство читателей. Начнем с самого простого: Пример: Умножить матрицу
Пример сложнее: Умножить матрицу Формула:
В результате мы получили так называемую нулевую матрицу. Попробуйте самостоятельно выполнить умножение Обратите внимание, что
Таким образом, переставлять матрицы в произведении нельзя! Если в задании предложено умножить матрицу M на матрицу N, то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот.
Примеры с матрицами третьего порядка: Умножить матрицу Формула умножения очень похожа на предыдущие формулы:
А теперь попробуйте самостоятельно разобраться в умножении следующих матриц: Умножьте матрицу Вот готовое решение, но постарайтесь сначала в него не заглядывать!
Нахождение обратной матрицы Смотри, после вычисления определителей, раздел 2.3.
Вычисление определителей
В ходе решения задач по высшей математике очень часто возникает необходимость вычислить определитель матрицы. Определитель матрицы фигурирует в линейной алгебре, аналитической геометрии, математическом анализе и других разделах высшей математики. Таким образом, без навыка решения определителей просто не обойтись. Мы не будем давать строгое математическое определение определителя, и, вообще, будем стараться минимизировать математическую терминологию, так как большинству читателей легче от этого не станет. Наша задача – научить Вас решать определители второго, третьего и четвертого порядка. Весь материал изложен в простой и доступной форме, и даже полный (пустой) чайник в высшей математике после внимательного изучения материала сможет правильно решать определители. Определение: Определитель, или детерминант матрицы, – это единственное для данной матрицы число, оно определяется всеми элементами матрицы и характеризует всю матрицу. Определитель можно вычислить только для квадратной матрицы. Для вектора таким характерным числом является модуль вектора. Для действительного числа произвольного знака таким характерным числом является абсолютное значение, или модуль числа. Но, в отличие от модуля ненулевого вектора или числа, определитель матрицы может иметь любой знак и быть равным нулю, в том числе для ненулевой исходной матрицы. Обозначение: Определитель матрицы обозначается символом данной матрицы в прямых (одинарных, или двойных) скобках, как у модуля вектора, или D, или Δ, или det(A). Т. е., как | A |, или || A ||, или латинской буквой D, или греческой буквой Δ, или det(A) для матрицы A. При этом вместо A в новые скобки может быть вписана вся таблица. На практике чаще всего можно встретить определитель второго порядка, например: Определитель четвертого порядка Надеюсь, всем понятно следующее: Числа внутри определителя живут сами по себе, и ни о каком вычитании в строке или столбце D речи не идет. Менять местами числа нельзя! Но если очень хочется, то можно... (На самом деле, есть десяток теорем о детерминантах, об условиях, при которых можно переставлять строки и столбцы, но не отдельные элементы, определителя со сменой (или без смены) знака определителя). Таким образом, если дан определитель, то ничего внутри него не трогаем!
1) Что значит вычислить (найти, раскрыть, решить) определитель? Вычислить определитель – это значит НАЙТИ ЧИСЛО. Знаки вопроса (?) в вышерассмотренных примерах – это совершенно обыкновенные числа. 2) Теперь осталось разобраться в том, КАК найти это число. Как Вы догадываетесь, для этого нужно применить определенные правила, формулы и алгоритмы.
Определитель матрицы «два на два», его формула:
ЭТО НУЖНО ЗАПОМНИТЬ, по крайней мере, на время изучения высшей математики в ВУЗе. Сразу рассмотрим пример:
Готово. Самое главное, НЕ ЗАПУТАТЬСЯ В ЗНАКАХ.
Определитель матрицы «три на три», его формула:
Пример:
Приведенная формула определителя «три на три» длинная и допустить ошибку по невнимательности проще простого. Как избежать промахов? Определитель «три на три» можно раскрыть 10 способами (10-ю способами получить приведённую формулу). Четыре из них – «простые», и шесть – «нормальные».
Начнем с четырёх простых способов «параллельных полосок» Саррюса: 1) два способа дополнительных столбцов; 2) два способа дополнительных строк. Первый способ дополнительных столбцов состоит в том, что справа от определителя приписывают первый и второй столбцы и аккуратно карандашом проводят линии:
Заметим, что элементы на «красных» диагоналях входят в формулу со знаком «плюс», а элементы на «синих» диагоналях входят в формулу со знаком минус.
Пример:
Второй способ дополнительных столбцов состоит в том, что слева, перед определителем приписывают второй и третий (ближе к определителю) столбцы и проводят линии, начиная с главной диагонали.
Первый способ дополнительных строк состоит в том, что снизу от определителя приписывают первую (ближе к определителю) и вторую строки и проводят линии, начиная с главной диагонали.
Второй способ дополнительных строк состоит в том, что сверху от определителя приписывают вторую и третью (ближе к определителю) строки и проводят линии, начиная с главной диагонали.
Во всех четырёх простых способах элементы матрицы, находящиеся на «красных» диагоналях, параллельных главной диагонали, входят в формулу со знаком «плюс». Элементы матрицы, находящиеся на «синих» диагоналях, входят в формулу со знаком минус. Вычисления по остальным простым способам проведите самостоятельно.
Сравните решение «по формуле» и «простые решения». Нетрудно заметить, что это ОДНО И ТО ЖЕ, просто во втором случае немного переставлены множители формулы, и, самое главное, вероятность допустить ошибку значительно меньше.
Теперь рассмотрим 6 «нормальных» способов для вычисления определителя. Почему «нормальных» Потому что в подавляющем большинстве случаев определители требуется раскрывать именно так. Как Вы заметили, у определителя «три на три» три столбца и три строки. Вычислить определитель можно, разложив его по любой строке или по любому столбцу. Таким образом, получается 6 способов, при этом во всех случаях используется алгоритм одного и того же типа (смотрите в книгах по высшей алгебре теорему Лапласа о разложении определителя матрицы по любой строке или столбцу, но мы обещали нашим студентам «не докучать моралью строгой»). Теорема Лапласа: Определитель матрицы равен сумме произведений элементов строки (столбца) на соответствующие алгебраические дополнения. Страшно? Все намного проще, будем использовать ненаучный, но понятный подход, доступный даже для человека, далекого от математики. В следующем примере будем раскрывать определитель по первой строке. Для этого нам понадобится «матрица знаков»: Примечание: Внимание! «Матрица знаков» – это изобретение. Данное понятие не научное, его не нужно использовать в чистовом оформлении заданий, оно лишь помогает вам понять алгоритм вычисления определителя. Сначала приведём полное решение. Снова берем наш подопытный определитель и проводим вычисления по теореме Лапласа, разложив его по первой строке:
И главный вопрос: КАК из определителя «три на три» получить вот это вот:
Итак, определитель «три на три» сводится к решению трёх маленьких определителей, или, как их еще называют, МИНОРОВ. Термин надо запомнить. Минор – маленький, точнее, по смыслу в данном случае, - определитель уменьшенной матрицы.
Коль скоро выбран способ разложения определителя по первой строке, очевидно, что всё вращается вокруг неё. Запишем рядом исходную матрицу и «матрицу знаков», одинаковую для любой матрицы «три на три»:
Элементы обычно рассматривают слева направо (или сверху вниз, если был бы выбран столбец). Сначала разбираемся с первым элементом строки, то есть с единицей:
1) Из матрицы знаков выписываем соответствующий знак:
2) Затем записываем сам элемент:
3) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит первый элемент:
Оставшиеся четыре числа и образуют определитель «два на два», который называется МИНОРОМ данного элемента (единицы).
Переходим ко второму элементу строки.
4) Из матрицы знаков выписываем соответствующий знак:
5) Затем записываем второй элемент:
6) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит второй элемент:
Оставшиеся четыре числа записываем в маленький определитель.
Переходим к третьему элементу первой строки. Никакой оригинальности:
7) Из матрицы знаков выписываем соответствующий знак:
8) Записываем третий элемент:
9) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит третий элемент:
Оставшиеся четыре числа записываем в маленький определитель.
Остальные действия не представляют трудностей, поскольку определители «два на два» мы считать уже умеем. НЕ ПУТАЕМСЯ В ЗНАКАХ!
Аналогично определитель можно разложить по любой строке или по любому столбцу. Естественно, во всех шести случаях ответ получается одинаковым. В этом и состоит ценность теоремы Лапласа!
Определитель «четыре на четыре» можно вычислить, используя этот же алгоритм. При этом матрица знаков у нас увеличится:
В следующем примере раскроем определитель по четвертому столбцу:
Пример:
А как это получилось, попробуйте разобраться самостоятельно. Если кто захочет прорешать определитель до конца, правильный ответ: 18. Для тренировки лучше будет также раскрыть определитель по какому-нибудь другому столбцу или другой строке.
Вычисление обратной матрицы
Что такое обратная матрица? Прежде определим единичную матрицу.
Определение: Единичной матрицей n-го порядка называется такая матрица En, что для любой квадратной матрицы n-го порядка An выполняется соотношение
Можно показать, что у единичной матрицы на главной диагонали расположены единицы, а все остальные элементы равны нулю.
Определение: Обратной матрицей для матрицы An с неравным нулю определителем (| A n | ¹0) называется такая матрица An -1, для которой выполняется соотношение
Что необходимо знать и уметь для успешного изучения данного материала? Ответ. Вы должны уметь вычислять определители. Вы должны понимать, что такое матрица и уметь выполнять некоторые операции с матрицами. Обратную матрицу A -1 можно найти по следующей формуле:
(Обозначение Ã читаем «A с тильдой»)
Понятие обратной матрицы, как и понятие определителя, существует только для квадратных матриц, матриц «два на два», «три на три» и т.д.
Обозначения: Как Вы уже, наверное, заметили, обратная матрица обозначается добавлением надстрочного индекса (-1) к символу исходной матрицы. Начнем с простейшего случая – матрицы «два на два». Чаще, конечно, требуется найти обратную матрицу для матрицы «три на три», но мы настоятельно рекомендуем изучить более простое задание, чтобы усвоить общий принцип решения. Пример: Найти обратную матрицу для матрицы Решаем. Последовательность действий удобно разложить по пунктам.
1) Сначала находим определитель матрицы.
Важно! У матрицы, определитель которой равен НУЛЮ, обратной матрицы НЕ СУЩЕСТВУЕТ (Это следствие из основной теоремы об обратной матрице). В рассматриваемом примере, как выяснилось, | A | = -2 ¹ 0, а значит, всё в порядке.
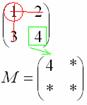
2) Находим матрицу миноров элементов. Матрица миноров элементов имеет такие же размеры, как и матрица A, то есть, в данном случае,
Дело за малым, осталось найти четыре числа и поставить их вместо звездочек. Возвращаемся к нашей матрице
Как найти минор этого элемента матрицы? А делается это так: МЫСЛЕННО вычеркиваем строку и столбец, в котором находится данный элемент:
Оставшееся число в данном случае и является минором данного элемента, которое записываем в нашу матрицу миноров:
Рассматриваем следующий элемент матрицы
Мысленно вычеркиваем строку и столбец, в котором стоит данный элемент:
То, что осталось, и есть минор данного элемента, который записываем в нашу матрицу:
Аналогично рассматриваем элементы второй строки и находим их миноры:
Готово.
3) Находим матрицу алгебраических дополнений соответствующих элементов. Это просто. В матрице миноров нужно ПОМЕНЯТЬ ЗНАКИ у двух чисел:
4) Находим транспонированную матрицу алгебраических дополнений.
Ответ. Вспоминаем нашу формулу Всё найдено! Таким образом, искомая обратная матрица:
Ответ лучше оставить в таком виде. НЕ НУЖНО делить каждый элемент матрицы на 2, так как получатся дробные числа.
Как проверить решение? По определению обратной матрицы, необходимо выполнить матричное умножение
6) Проверка:
Получена так называемая единичная матрица (с единицами по главной диагонали и нулями в остальных местах). Таким образом, обратная матрица найдена правильно.
Перейдём к более распространенному на практике случаю – матрице «три на три».
Пример: Найти обратную матрицу для матрицы
Алгоритм точно такой же, как и для случая «два на два».
Обратную матрицу найдем по формуле:
|
|||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 2379; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.015 с.) |

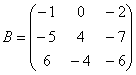 .
.
 .
.



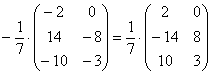

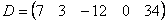 .
. .
.


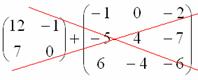 - Такое действие не определено для этих матриц!
- Такое действие не определено для этих матриц! и
и 
 .
. и
и  .
.

 на матрицу
на матрицу  ?
?
 , значит, умножать данные матрицы можно.
, значит, умножать данные матрицы можно.
 , значит, выполнить умножение нельзя, и, вообще, такая запись не имеет смысла:
, значит, выполнить умножение нельзя, и, вообще, такая запись не имеет смысла:
 и
и 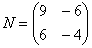 существует как произведение
существует как произведение  , так и
, так и  .
. на матрицу
на матрицу  – попытайтесь сразу уловить закономерность. Поэтому:
– попытайтесь сразу уловить закономерность. Поэтому:
 . В таком случае произведение:
. В таком случае произведение: .
. .
. ! Это почти всегда так!
! Это почти всегда так! на матрицу
на матрицу  .
.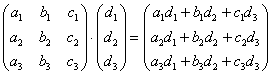
 .
. .
. .
. , и определитель третьего порядка, например:
, и определитель третьего порядка, например:  .
.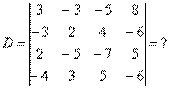 встречается значительно реже, но о нем тоже поговорим.
встречается значительно реже, но о нем тоже поговорим. .
.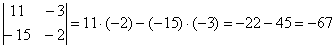

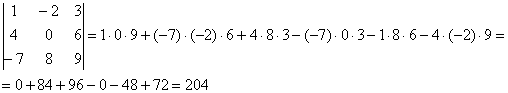
 .
.
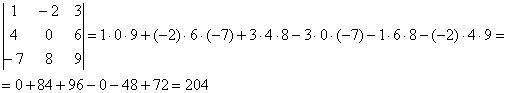
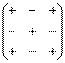 . Легко заметить, что знаки расположены в шахматном порядке.
. Легко заметить, что знаки расположены в шахматном порядке.
 ?
?








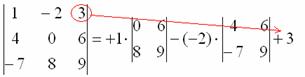



 .
. .
. где | A | – определитель матрицы A, Ã – матрица алгебраических дополнений исходной матрицы, а ÃT – присоединённая матрица, или транспонированная матрица алгебраических дополнений соответствующих элементов матрицы A.
где | A | – определитель матрицы A, Ã – матрица алгебраических дополнений исходной матрицы, а ÃT – присоединённая матрица, или транспонированная матрица алгебраических дополнений соответствующих элементов матрицы A. .
. .
. .
. .
.
 :
:




 – это и есть матрица миноровсоответствующих элементов матрицы A.
– это и есть матрица миноровсоответствующих элементов матрицы A. . Именно у тех чисел, которые обведены в кружок! Получим:
. Именно у тех чисел, которые обведены в кружок! Получим: - это матрица Ã алгебраических дополнений соответствующих элементов матрицы A.
- это матрица Ã алгебраических дополнений соответствующих элементов матрицы A. - это транспонированная матрица алгебраических дополнений соответствующих элементов матрицы A.
- это транспонированная матрица алгебраических дополнений соответствующих элементов матрицы A.
 либо
либо  .
.
 .
. , где
, где  – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы B.
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы B.


