Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование неправильной дробно-рациональной функцииСодержание книги
Поиск на нашем сайте
Перейдем к рассмотрению случая, когда старшая степень числителя больше либо равна старшей степени знаменателя.
Пример 8 Найти неопределенный интеграл
Совершенно очевидно, что данная дробь является неправильной, так как 4>3. Основной метод решения интеграла с неправильной дробно-рациональной функций – это деление числителя на знаменатель. Да-да, делить будем столбиком, как самые обычные числа в школе. Напоминаю алгоритм. Сначала рисуем «заготовку» для деления:
ВСЕ недостающие степени (и (или) свободные члены) без пропусков записываем в ОБОИХ многочленах с нулевыми коэффициентами. Теперь маленькая задачка: на какой множитель нужно умножить
Далее умножаем
Проводим черточку и производим вычитание (из верха вычитаем низ):
Старшая степень остатка Итак, наше решение принимает следующий вид:
Делим числитель на знаменатель:
(1) Что дало деление? Много хорошего: теперь у нас два слагаемых, первое интегрируется совсем просто, а второе – правильная дробь, которую мы решать уже умеем. После деления всегда желательно выполнять проверку. В рассматриваемом примере можно привести к общему знаменателю выражение
и в результате получится в точности исходная неправильная дробь
(2) От первого слагаемого сразу берем интеграл. Знаменатель дроби раскладываем на множители Дальше всё идет по накатанной схеме: Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
Готово.
И, наконец, заключительный пример для самостоятельного решения. Он очень интересен, рекомендуем всем!
Пример 9 Найти неопределенный интеграл
Заметим, что во всех примерах урока в ходе решения систем у нас получались «хорошие» целые коэффициенты A, B и C. Это происходило по той причине, что почти все интегралы были взяты из сборника задач по высшей математике для экономистов. На практике же часто будут появляться разные нехорошести. Таким образом, если в ходе решения интеграла от дробно-рациональной функции у Вас получаются дробные значения коэффициентов A, B, C,…, то в этом нет ничего страшного, ситуация даже обыденна. Решения и ответы: Пример 2: Решение:
Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
Комментарий. В правой части у нас нет слагаемого с x2, поэтому в первом уравнении системы ставим справа ноль.
Пример 4: Решение:
Шаг 1. Проверяем, правильная ли у нас дробь? Старшая степень числителя - 6. Старшая степень знаменателя - 8. Так как 6<8, то дробь является правильной. Шаг 2. Можно ли что-нибудь разложить в знаменателе на множители? Множитель (x2 +4) разложить нельзя, а вот (x2-4) – можно:
Шаг 3. Представим дробно-рациональную функцию в виде суммы элементарных дробей. В данном случае, разложение имеет следующий вид:
Пример 6: Решение:
Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
Пример 7: Решение:
Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
Пример 9: Решение:
(1) Здесь неправильная дробь, поскольку старшие степени числителя и знаменателя равны: 3 = 3. Для того чтобы разделить числитель на знаменатель придётся временно раскрыть скобки в знаменателе. (2)-(3) Теперь можно разделить числитель (4) От первого слагаемого сразу берем интеграл. Знаменатель оставшейся, уже правильной, дроби снова записываем в виде произведения множителей. Тут я немного сокращено разложение, надеюсь, всем понятно, что Далее очевидно… Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
Интегрирование корней (иррациональных функций). Примеры решений
Интегрирование иррациональных функций можно изучать уже при некоторых знаниях и навыках решения неопределенного интеграла. Такие образом, если Вы чайник, и за плечами всего десяток вычисленных интегралов, да и с методом замены переменной в неопределенном интеграле не очень, то лучше начать со статьи Неопределенный интеграл. Примеры решений. Хотя, не пугаемся, не разбегаемся – простейшие примеры с квадратными корнями, думаем, будут понятны широкому кругу студентов. Весь материал мы постараемся изложить максимально подробно и максимально просто. Мы разберем простейшие неопределенные интегралы от иррациональных функций, чуть более громоздкие, чем были до сих пор (с разными корнями), и закончится повествование биномиальными интегралами, кои уже являются немного дебрями интегралов.
|
||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 290; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.32.53 (0.006 с.) |

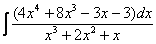 .
.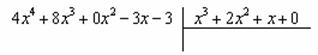 .
.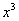 , чтобы получить
, чтобы получить 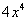 ? Очевидно, что на
? Очевидно, что на  :
: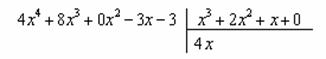
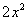 , потом – на
, потом – на 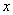 , потом – на 0 и записываем результаты слева:
, потом – на 0 и записываем результаты слева: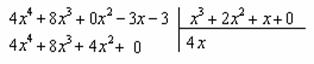

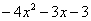 равна двум, старшая степень делителя
равна двум, старшая степень делителя 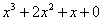 – больше, она равна трём, значит, больше разделить не удастся. Если бы изначально у нас был в числителе многочлен пятой степени, то алгоритм деления увеличился бы на один шаг.
– больше, она равна трём, значит, больше разделить не удастся. Если бы изначально у нас был в числителе многочлен пятой степени, то алгоритм деления увеличился бы на один шаг.
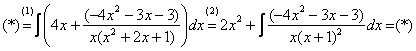 .
.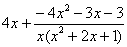 ,
,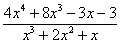 .
.
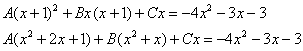
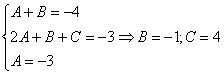 .
.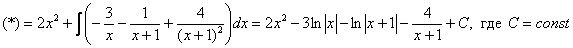
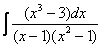 .
.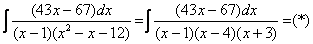
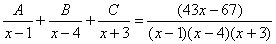 ;
; ;
; 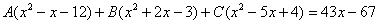 ;
; .
. .
.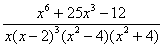
 .
.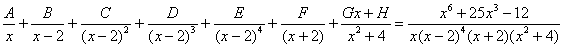
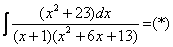 .
. .
. .
.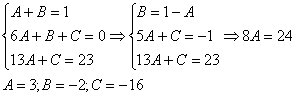 .
.
 .
.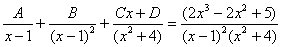 .
.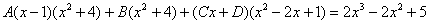 .
.

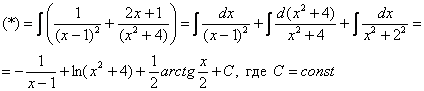
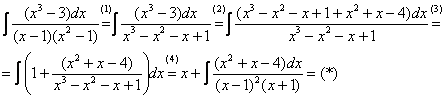
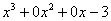 н а знаменатель
н а знаменатель  , но делать этого… я не буду. Можно поступить хитрее. Прибавим и вычтем из числителя выражение: (-x2-x+1).
, но делать этого… я не буду. Можно поступить хитрее. Прибавим и вычтем из числителя выражение: (-x2-x+1). .
.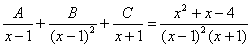 .
.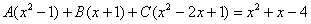 .
.